100种分析思维模型之：概率思维

你好，我是林骥。

下面介绍 100 种分析思维模型的第 53 种：概率思维。

一、为什么学习概率思维？

在我们的日常工作、生活和学习中，充满了各种不确定性，并且需要做出各种各样的决策。

比如，选择做什么事，和谁结婚，看哪本书 ……

而决策的质量，影响着工作是否顺利、生活是否幸福、学习是否进步 ……

另外，当今的科技前沿，包括大数据、GPT以及背后的人工智能等技术，都与概率有着密切的关系。

学会运用概率思维，可以帮助我们更好地理解现状、分析原因和预测未来，进而做出更加明智的决策，选择去做大概率正确的事情，比如深度学习、用心写作等。

二、什么是概率思维？

概率思维的本质，是通过观察和分析历史的数据，发现事物背后发展的规律，从不确定性中找到确定性，把局部的随机性转变为整体上的确定性，以提升未来成功的概率。

在刘润写的《底层逻辑 2》这本书中，介绍了 6 种不同的思维视角：战术、战略、模式、创新、时间和概率，其中概率属于最高的维度。

站在不同的高度看世界，看到的景象会有很大的差异。站在 100 层的人，可以俯瞰世界的气概，感觉风景尽收眼底；站在 20 层的人，可以看到整体的轮廓，看到的几乎全是美景；站在 1 层的人，只能看到眼前的细节，可能是市井吵架、违章停车；而站在负 18 层的人，看到的都是问题，周围垃圾成堆。

一个人站在 100 层看到的风景，站在负 18 层是无论如何都看不到的，这不是视力好坏的问题，而是高度和角度的问题。

我们不妨从当前的一个「点」出发，把当下做到极致，然后在心中有一条通往目标的「线」，朝着这条线的方向前进，避免用战术的勤奋，掩盖战略的懒惰，就能成功到达目的地。

有些人心中没有目标，盲目地追逐热点，最终把自己活成了一个漂泊的「点」，脚下的「线」指向了错误的方向，即使再努力，最后也很难抵达终点。

如果你能把所有的线路都看清楚，就像拿着一张二维的平面地图，这张地图相当于真实世界对应的模型，你可以根据目的地和个人偏好来选择最优的线路，这样就更容易到达目的地。

但二维的平面地图存在一个缺陷，就是不能分辨高架桥和地面的道路。要想解决三维立体的问题，我们还需要有创新思维。有些智能地图导航软件，可以让你选择是在高架桥还是在路面，并自动帮你切换到正确的线路上来。

如果你的战术、战略、模型和创新都做对了，那么剩下的就交给时间和概率，它们会给你结果。最终结果的好坏，还是要看概率，也就是人们常说的运气。很多成功的人，都会说自己是运气好。但一个人只要坚持去做大概率正确的事情，运气通常都不会太差。

当我们在观察事物的时候，加上时间和概率的维度之后，就能看到隐藏在事物背后各种周期性的规律。比如，客户生命周期、产品生命周期、企业生命周期、技术发展周期，等等。

三、怎么运用概率思维？

运用概率思维，就是预估不同结果发生的概率，进而更好地应对未来的不确定性。

比如，一家服装店的衣服，有不同颜色和尺码，应该如何适当配货？

假如平均分配，可能会导致有些颜色和尺码供不应求，另外一些颜色和尺码库存积压，怎么办？

如果你能对历史数据进行分析，统计出不同颜色和尺码的销售比例，结合客户特征、市场行情等情况，就能大致预测未来的销量，进而优化商品的配比，减少库存的积压，提升盈利的概率。

面对五花八门的数据，我们要注意避免产生「认知偏差」，特别是要注意「幸存者偏差」。

比如，在分析影响公司发展的因素时，我们可能只关注那些存活下来的公司做对了什么，而忽视了那些已经倒闭的公司做错了什么。

要想避免产生认知偏差，我们收集的历史数据就要能客观反映事物的全貌，而不能以偏概全，以免对未来作出错误的判断。

在概率论中，有一个「大数定律」，也就是在试验条件不变的情况下，重复试验多次，随机事件发生的频率会接近于它的概率。

比如，在掷硬币的游戏中，出现正面的概率是 50%，在掷了很多次之后，正面朝上的次数就会接近一半。

历史上，有很多数学家本着求真务实、探索真理的精神，真的掷了很多次硬币，并把结果记录了下来，这个小心求证的过程虽然枯燥乏味，但看到实验结果与理论相符，可以让我们对理论多一份信心。

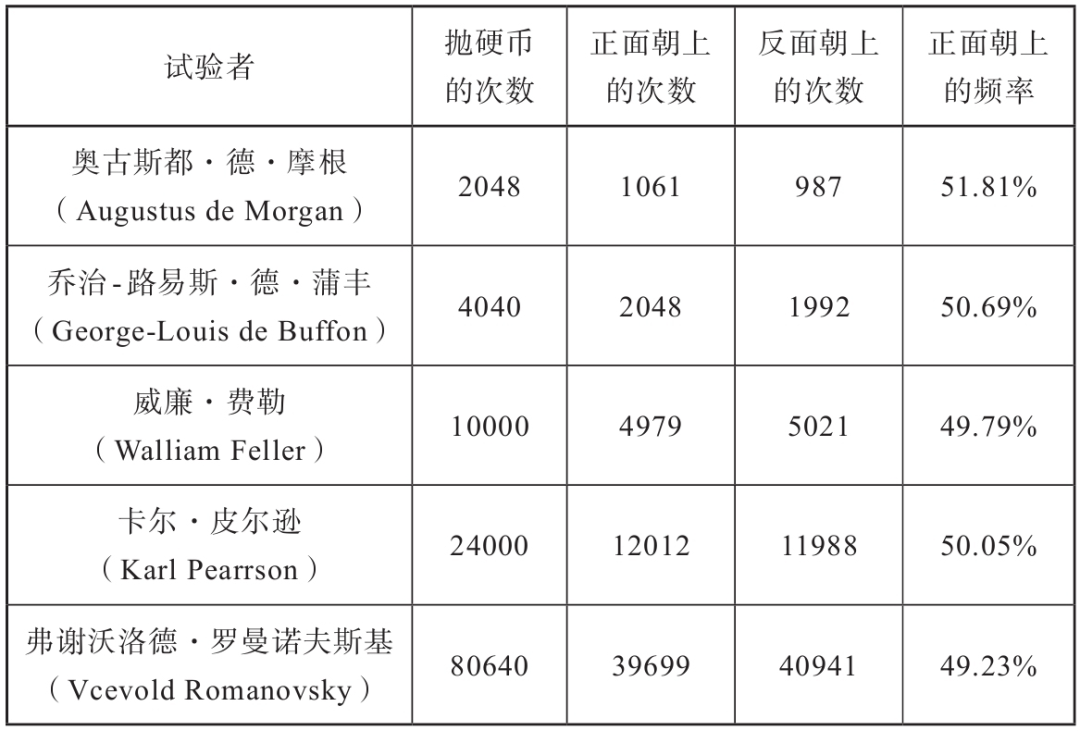
上述验证的方法是运用归纳思维，无法保证适用于所有的情况，要想排除例外情况，我们还需要运用演绎思维，基于逻辑推理进行严格证明。在数学家的努力下，从理论上成功证明了「大数定律」，因此也叫「大数定理」。

有了「大数定理」作为支撑，我们就有了理论的基础，因此可以放心地用大数据去解决问题，学会把目光看得更长远，重复去做那些大概率正确的事情，只要持续的时间足够长，未来大概率就能取得更大的成就。

假设做一件事成功的概率是 20%，重复做 5 次之后，至少成功一次的概率是多少呢？

我们可以运用《数据化分析》中介绍的逆向思维，反过来想一想，假设每次失败的概率都是 80%，在不考虑重复做事可以积累经验并提高概率的情况下，重复做 5 次之后，每次都失败的概率是 80% 的 5 次方，约等于 32.8%，也就是说，至少成功一次的概率约为 67.2%。

按照同样的方法，我们可以计算出：重复做 10 次之后，至少成功一次的概率是 89.3%；重复做 20 次之后，至少成功一次的概率是 98.8%。为了更加直观地展现上面概率的变化，我们可以用 GPT 来生成一段画图的 Python 代码，给 ChatGPT 发送以下指令：

假设你是一名资深数据分析师，需要用 Python 画一张图，展现做一件事的重复次数与成功概率的变化，假设做一件事成功的概率是 20%，随着重复次数的增加，成功的概率也在不断增加，请给出具体的 Python 代码。

ChatGPT 的回复如下：

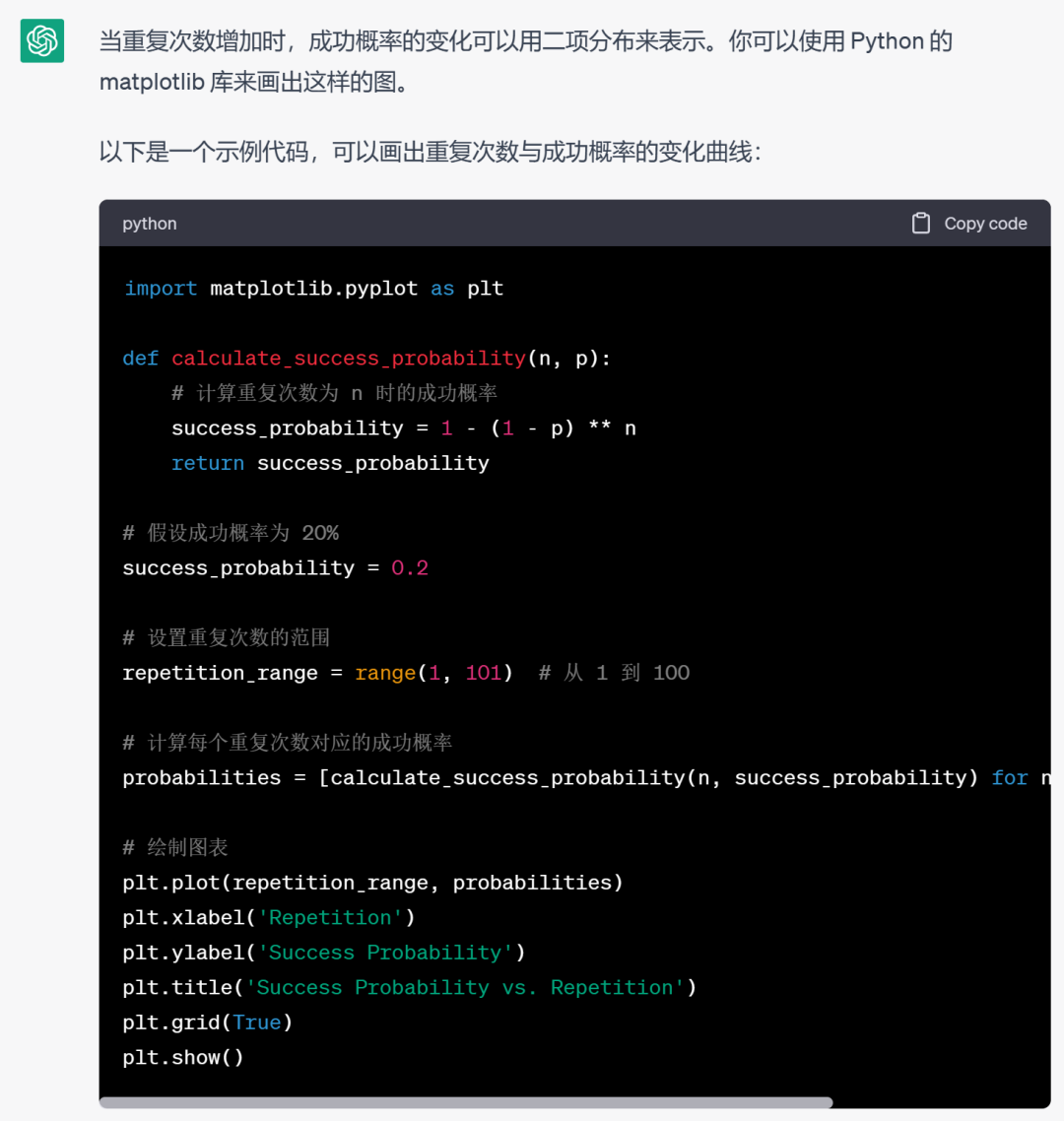
把上面的代码复制到 Jupyter Notebook 中，设置重复次数的范围从 1 到 20，运行就能得到下面的图片：

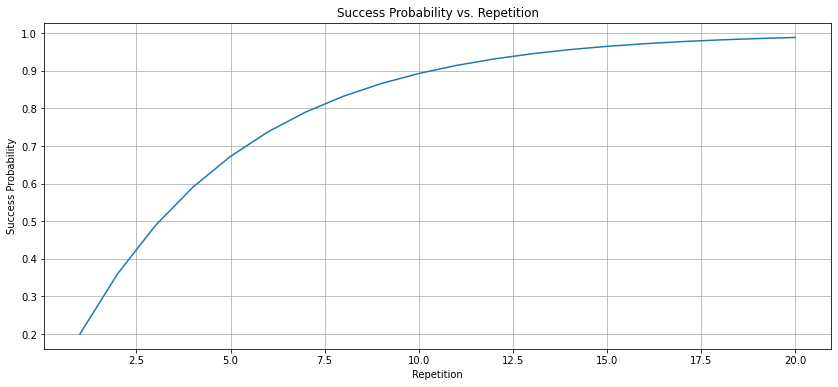
从图中可以直观地看出，随着重复次数的增加，成功的概率会逐渐接近于 100%。

假设做一件事成功的概率是 1%，重复做 100 次之后，至少成功一次的概率是多少呢？

答案是 63.4%。

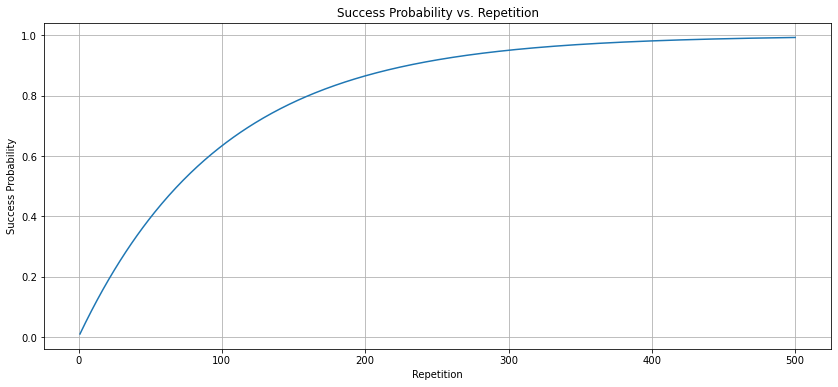
可以看出，当一件事成功的概率降低时，需要重复的次数将会明显增加。但一个人的时间总是有限的，我们不可能无限次地重复下去。

所以，我们应该在一个领域内持续深耕，积累足够长的时间，并重复足够多的次数，再加上经验的积累，就能提高成功的概率，这就是概率思维带给我们的启发。

另外，需要特别注意的是，概率往往也是有条件的。当条件具备的时候，小概率事件也可能变成大概率事件；反之，当条件不具备的时候，大概率事件也会变成小概率事件。

很多人生搬硬套别人的成功经验，结果发现自己却失败了，可能就是因为条件不一样。

四、最后的话

每种思维和工具都有其局限性和适用的边界。严格来说，所有模型都是错的，但其中有些是有用的。

我们不妨大胆进行尝试，用不同的思维模型去解决一些实际的问题，并在实践中小心检验，记录和总结一些行之有效的方法，不断丰富自己的「武器库」。查理·芒格说：

手拿铁锤的人，看什么都像钉子。

很多人不思进取，容易陷入思维僵化的怪圈，手里拿着一把锤子，到处去碰钉子，试图用一种方法去解决所有的问题。

他们的专业能力也许很强，但是却容易钻牛角尖，不知道这个世界还有很多其他的工具，比如斧头、钳子、锯子、尺子、镰刀 ……

准确地定义问题，是采取行动的起点，也是实现目标的关键。

当我们遇到问题的时候，用更适合它的思维和工具去解决，这样才能起到事半功倍的效果。

与其靠经验和直觉做出判断，不如运用概率思维，在一个专业领域持续深耕，并适当尝试一些新的事物，从数据中发现一些有用的规律，去发现问题、分析问题和接近问题，逐渐接近事实的真相。

公众号：林骥，《数据化分析》作者

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！