约瑟夫环问题详解（图文结合）--C语言
目录
约瑟夫小故事：
问题数学化：
特殊情况：
1. q = 2 , n =2^k (k=1 , 2, 3, ...... )
2. q = 2 , n =2^k + t (k=1 , 2, 3, ...... )
一般情况：
思路总结：
算法推导：
代码实现：
总结：
约瑟夫小故事：
约瑟夫是犹太军队的一个将军，在反抗罗马的起义中，他所率领的军队被击溃，只剩下残余的部队40余人，他们都是宁死不屈的人，所以不愿投降做叛徒。一群人表决说要死，所以用一种策略来先后kill所有人。
于是约瑟夫建议：每次由其他两人一起kill一个人，而被kill的人的先后顺序是由抽签决定的，约瑟夫有预谋地抽到了最后一签，在kill了除了他和剩余那个人之外的最后一人，他劝服了另外一个没死的人投降了罗马。
问题数学化：
现在有 n 个人，每个人都有属于自己的标识（下标），分别是 0 ~ n-1。所有人呈圆环状排列，每隔 q 个人就淘汰一个人 ，最后只能有一个人留下来，来求这个人的下标。
特殊情况：
1. q = 2 , n =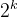 
(k=1 , 2, 3, ...... )
此时的存活的人总是第一个人！
例如：
注：本文所有图中的黑色数字都代表人物的报号数
2. q = 2 , n = 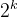+ t (k=1 , 2, 3, ...... )
此时存活的总是第（2t+1）个人！
例如：
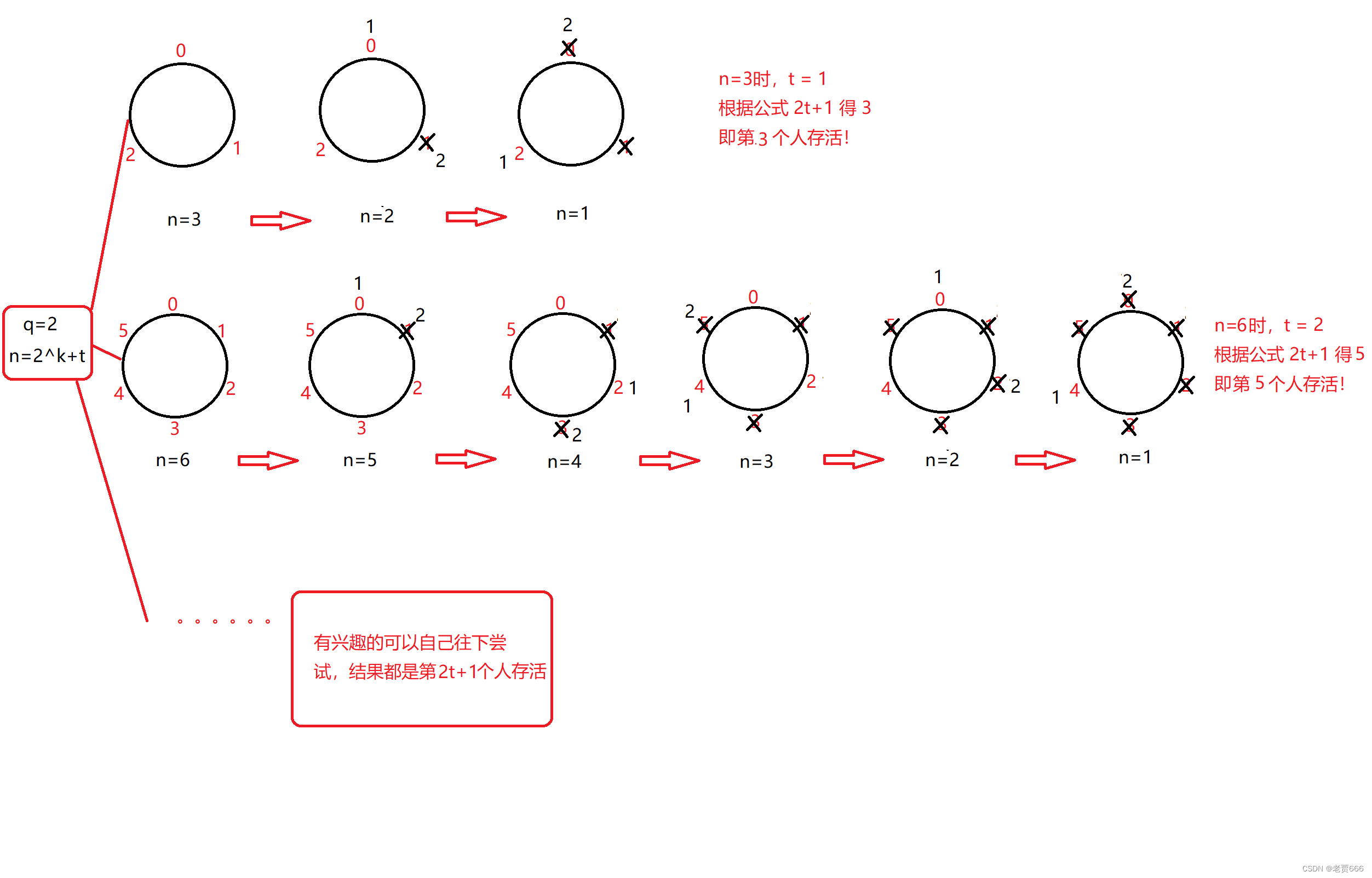
其实这里的第二种特殊情况可以利用上面第一种特殊情况来理解！
我们不妨这样想： + t 比
多出来了t 个人，那么如果先淘汰掉 t 个人，剩下的不就变成
个人时的问题了吗？也就是淘汰掉第 t 个人时的下一个人就是最后存活下来的人。这是问题就转化成找淘汰第 t 个人的下标了。
显然当 q=2时，第 t 个人的下标就是 2t - 1（这里读者老爷们可以自己用实际数据来推），那么其下一个人的下标就是 2t 了，也就是第 2t+1 个人最后存活下来啦！
这样公式的推导就明明白白了。
一般情况：
好了，到这里我们就不能靠着特殊情况的优势来分析问题了。
除了上述思路外，我们不妨以参与游戏的人物的角度来看这个游戏！（对于每轮结束后更新下标的做法理解起来更方便一点）
当淘汰一个人之后，本轮游戏结束，进入下一轮，紧接着上个被淘汰的人的下一个人就会想：“现在从我开始重新报号了，在剩下的人当中，我现在就相当于第一个人了，我的下标就是0了，只要 q != 1，我就不会被淘汰！”
此时剩下的其他玩家也会有相同的思考过程。因此他们的下标也会相应的基于上一轮的下标做出改变。
游戏进行下去，每淘汰一个人，人物在心里面都会对自己的下标及时更新，看看自己是否平安无事。
这样的心理变化直到最后只剩一个人游戏结束时才会停止。
当最后只剩下张三一个人时，他禁不住会思考：我现在的下标是0，那么我上一轮的下标是多少呢？我上上一轮的下标是多少呢？......
张三最后恍然了：我最初的下标是多少呢？！
好问题！
思路总结：
总结上述，其实我们要做的就是根据本轮的下标来逆推上一轮的下标。最为重要的是：我们知道最后一轮留下的那个人的下标！就是0！因此，把每轮之间的下标规律找到后，就可以由第一轮逆推出想要的第 n 轮的下标。
算法推导：
这里我先举一个简单的例子来总结规律：
假设 q=3
由 n=6 到 n=5 时，每个玩家的下标变化：
new = (n + old - q) % n;
old=(new + q) % n;
这里的计算公式可以观察简单少量的数据试出来，也可以利用数学思维来试着总结。
由于不太好用文字描述，各位读者老爷可以根据上面的实例来试着理解。
哈哈哈，有了公式，我们就可以嚣张起来了。也就是说，我们可以从最开始的 0 下标利用公式逐层往上查找，直到我们想要的那一层为止！
下面是完整的推理过程：
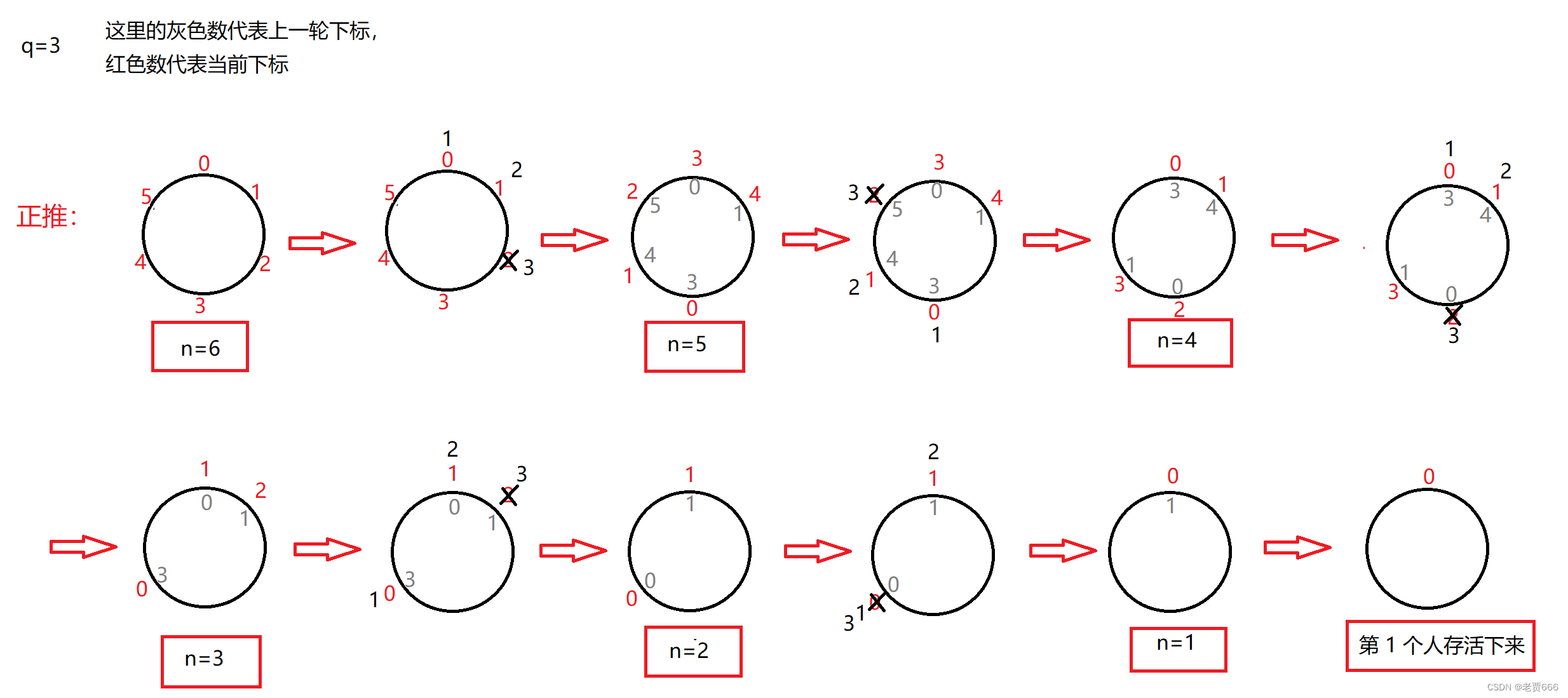
代码实现：
#include
int main()
{//最初的下标s为0int n,q,s=0;scanf("%d%d", &n, &q);for (int i = 2; i <= n; i++){s = (s + q) % i;}//s是最后存活的下标printf("%d\n", s + 1);return 0;
} 总结：
约瑟夫环这类问题用到的思想就是从第 n-1 个问题 推出第 n 个问题 。逐层解决问题是一大亮点。
运用公式来计算会使整个代码简单许多，只要在逻辑上理解了，那么公式才会运用的心安理得和得心应手！
好啦，这次分享就到此为止了。关于上面的文章有什么不懂的地方，大家可以在评论区下方留言哦！
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！