机器学习之逻辑回归算法
一、什么叫逻辑回归算法?
逻辑回归是一种用于二分类问题的机器学习方法,它通过一个名为sigmoid的函数(平滑函数)将线性回归的输出映射到0到1之间的概率值,从而进行分类。
尽管名字中包含“回归”,但实际上它是一种分类方法,主要用于二分类问题,同时也推广到了解决多分类问题。
逻辑回归模型的输出是一个概率值,通常,我们会设定一个阈值,当模型输出的概率大于这个阈值时,我们将样本判定为正类,否则判定为负类。
二、逻辑回归算法的原理
逻辑回归的原理就是将线性回归的输出结果通过平滑函数(Sigmoid函数)转换成0-1间的一个概率值。这个概率值为正分类的概率值。
平滑函数的示意图如下:
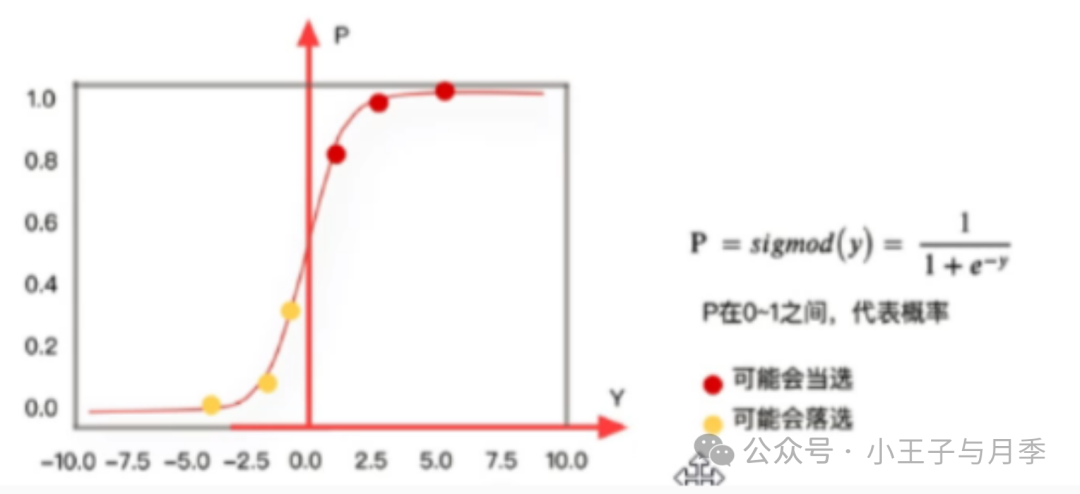
上面提到逻辑回归一定是在线性回归的基础上。线性回归的Y值分布,正常情况下属于二项分布,在出现样本数据极其不规则时我们认为Y值仍属二项分布。(二项分布的概念可自行了解)
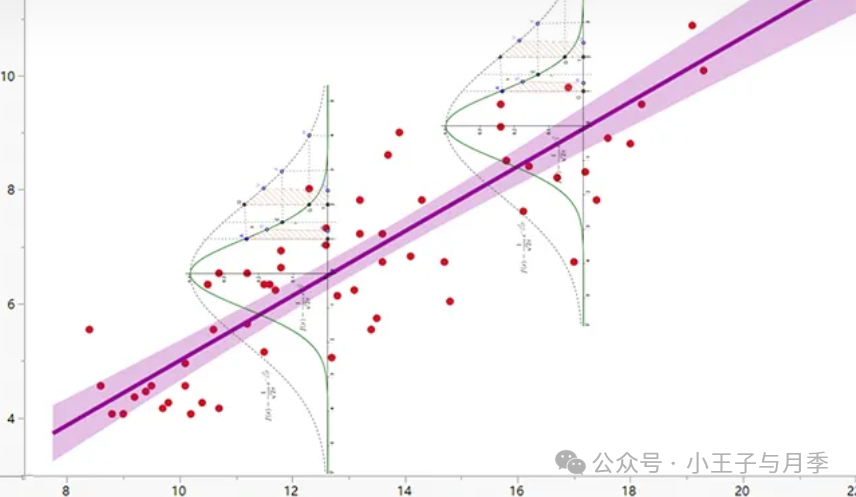
Y值属于正态分布
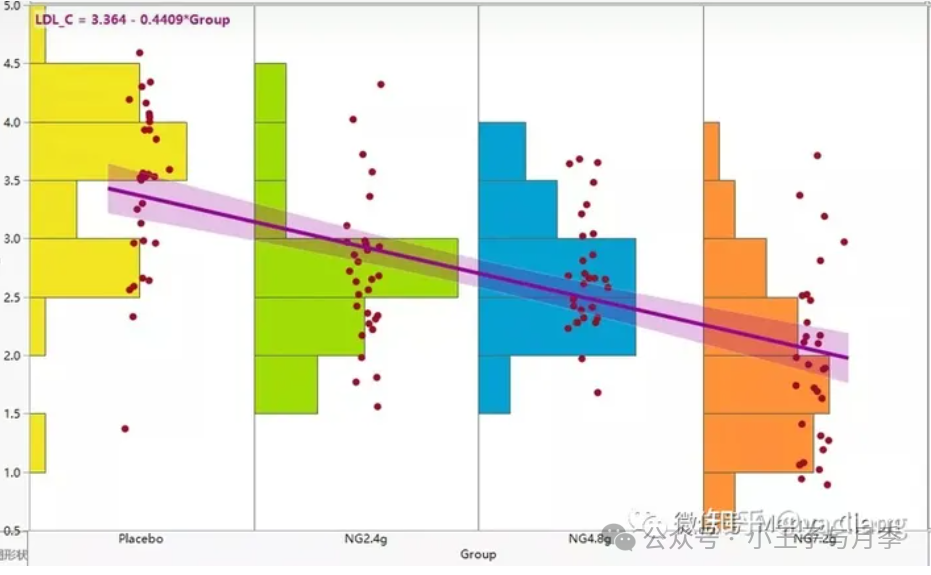
Y值属于二项分布
对于二项分布问题,如果某个事件发生的概率为 P ,那么该事件不发生的概率为 1−P,该事件的几率定义为发生概率与不发生概率的比值。我们取几率的自然对数(值可为负无穷大与正无穷大)映射为线性分布的y值。
ln(P/(1-P))=y 可得出平滑函数公式
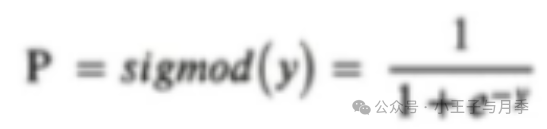
三、逻辑回归算法的应用步骤
1. 数据预处理
2. 确定线性回归模型的参数及Y值
定义一个线性回归模型,使用梯度下降法(GD)(或用最小二乘法)求得线性回归方程参数,然后计算出Y值。
3. 使用平滑函数计算出正类概率
4. 定义概率阈值
根据业务需求,设定一个概率阈值。
5. 预测结果
四、逻辑回归算法的适用边界和优缺点
1. 适用边界
逻辑回归算法适用于二分类问题,即数据只有两个类别。
对于多分类问题,我们可以使用多个逻辑回归模型来解决。此外,逻辑回归算法还要求数据满足一定的假设条件,比如特征之间是线性可分的,数据服从伯努利分布等。
2. 优点
- 简单容易实现。
- 运算效率比较高,适合处理大规模数据。
- 结果可解释性比较强。逻辑回归模型的结果可以转化为概率值,方便我们进行解释和分析。
3. 缺点
- 线性可分性:逻辑回归只能处理线性可分的问题,对于非线性可分的数据,逻辑回归的效果会很差。
- 处理多分类问题困难:逻辑回归通常只能处理二分类问题,对于多分类问题,需要进行一些额外的处理。
- 容易过拟合:如果样本量不足或特征过于复杂,逻辑回归容易过拟合。
- 对异常值敏感:逻辑回归对异常值较为敏感,特别是在特征空间较小的情况下,异常值可能对模型的性能产生较大影响。、
五、应用场景
线性回归模型主要是用来预测分析,逻辑回归模型是在线性回归基础上进行的,因此它也主要是用来预测,不过逻辑回归更多用来预测二分类而非具体的值。比如预测房价涨跌问题、预测用户性别、预测用户是否点击商品(页面)、预测用户是否购买指定商品等。更多场景如下:
- 信用评估:预测个人或企业的信用风险,帮助银行和金融机构进行信贷决策。
- 疾病预测:根据患者的临床特征和医学检测结果,预测患者是否患有某种疾病,如糖尿病、高血压等。
- 市场预测:预测市场趋势或产品销售量,帮助企业制定营销策略和业务决策。
- 欺诈检测:识别信用卡欺诈、网络诈骗等欺诈行为,帮助金融机构和电商平台提高安全性。
- 用户行为分析:预测用户的行为,如购买意愿、流失风险等,以优化个性化推荐和用户体验。
- 市场调研:分析市场调研数据,预测消费者对产品或服务的偏好和购买意愿。
- 网络点击率预测:预测广告或推广内容的点击率,帮助广告主优化广告投放策略。
- 人口统计学研究:分析人口统计数据,预测人口群体的行为和趋势,如选民投票行为、购买决策等。
作者:厚谦,公众号:小王子与月季
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
