运动与动画基础
一、运动动画的理论依据
“动画的一切皆在于时间点和空间幅度”——迪士尼动画大师格里穆·乃特维克曾经说过。
现实生活中的物体不仅会立即启动和停止,而且几乎不会以恒定速度移动;当我们打开抽屉时,我们首先快速移动它,并在它出来时放慢速度;在地板上放一些东西,它会先向下加速,然后在撞到地板后反弹回来。
运动动画的理论依据希望帮助设计师了解物理运动背后的科学知识。
1. 运动动画
我们先从最简单的运动动画说起。我们客观物理规律还是得从牛顿第二定律说起。
F=ma,如果大家不明白这个公式,没关系。
请允许我不那么讲究术语的严谨性,通俗点来说,就是运动动画响应变化情况与执行动画的物体本身有关;如果你想表现的物体是一个沉甸甸的,那么他们的起始动画响应/参数的变化会比较慢;反之,物体是轻巧的,那么其起始动画响应/参数的变化会比较快。

从图上可以看到如果是相同的操作且移动相同的距离,轻巧的所花的时间越短。
2. 阻尼动画
提到阻尼,需要介绍三个概念:临界阻尼、过阻尼、欠阻尼。
1)临界阻尼
生活中一些高档的门或橱柜,他们在开合的过程中为了不造成太大的声响,他们的机械结构阻尼会尽量设计接近临界阻尼;这个过程最容易让人接受,不会感觉有外界干扰;过阻尼和欠阻尼,通常能让你感觉到有一只隐形的手,阻碍或促进运动。
2)过阻尼
从字面上会容易理解,就是阻尼很大,阻碍运动的发展;有些自动门或电梯门在闭合的过程中,在最后段里往往需要更长的时间;另外,记忆枕的恢复的过程也是过阻尼。
3)欠阻尼
阻尼不够,继而形成了振荡的特征;生活中的一些弹簧门,在关闭的过程中,会多次摆动,最终趋于闭合。

做一个比较细腻的界面动画时候,如果追求理性一些,可以把动画的成果拆解成三个阶段:启动、运行、收尾;设计师需要花更多的时间去考虑启动与收尾过程。

启动阶段:体现力、质量、环境,可以表现材质的轻盈与厚重。
收尾阶段:体现质量、速度、环境;阻尼通常在这个阶段体现。
举个例子:
请大家关注启动与收尾阶段。


3. 呼吸动画
对于这个动画,设计师最直观的印象就是闪烁;在实施的过程中,对于闪烁一词会被赋予不同的理解。
设计师眼中的闪烁:“渐显 -> 渐隐 -> 渐显 -> 渐隐”;工程师眼中的闪烁:“显示 -> 隐藏 -> 显示 -> 隐藏”。
如何把动画做得更细腻,就在于如何将渐显与渐隐的过程如何描述得更加仔细。
对于最早的渐显、渐隐动画,首先想到了三角函数。

仔细观察这个函数,可以发现他的特点是在一个周期里是启动渐增、收尾减缓的过程,适合开发利用简单代码实现的动画效果;但,三角函数方式的顾虑总觉得哪里还是不太自然,看起来“呼吸比较急促”。
现在试试深呼吸,体会一下;你会发现在我们的在吸气的阶段,很快会就达到肺撑满的状态,然后吐气的阶段可以持续很久。
大体上比例分布是这样的:

融合入三角函数,将起始的渐增与收尾的减缓引入,例如下面的函数图形:

函数如下:

这个函数的周期为6,峰值出现在2。整个变化起始与收尾都是渐变过渡。
k=1/3,t=6, n={1,2,3,…}。
二、运动动画的动画曲线
1. 动画曲线展示
以上的运动形式都可以用动画曲线表示,easings罗列的动画曲线如下:

他们表述了动画变化的程度与时间的关系,通过合理利用这些动画曲线背后的原理,可以让动画看起来更加真实。
2. 动画曲线数据抽象
我们可以依据运动需求,通过数据定制特定时间的动画曲线。
1)cubic-bezier(必须要理解掌握的贝塞尔曲线)
cubic-bezier称为三次贝塞尔曲线,主要是生成速度曲线的函数。
规范:cubic-bezier(

从上图中我们可以看到,cubic-bezier有四个点:
两个默认的,即:P0(0,0),P3(1,1);两个控制点,即:P1(x1,y1),P2(x2,y2)。
注:X轴的范围是0~1,超出cubic-bezier将失效,Y轴的取值没有规定,但是也不宜过大。

我们只要调整两个控制点P1和P2的坐标,最后形成的曲线就是动画曲线。
cubic-bezier界面如下,可以在特定时间内的cubic-bezier运动曲线:

2)interpolator
cubic-bezier不能表示欠阻尼动画与呼吸动画,使用interpolator进行表示。
欠阻尼动画:
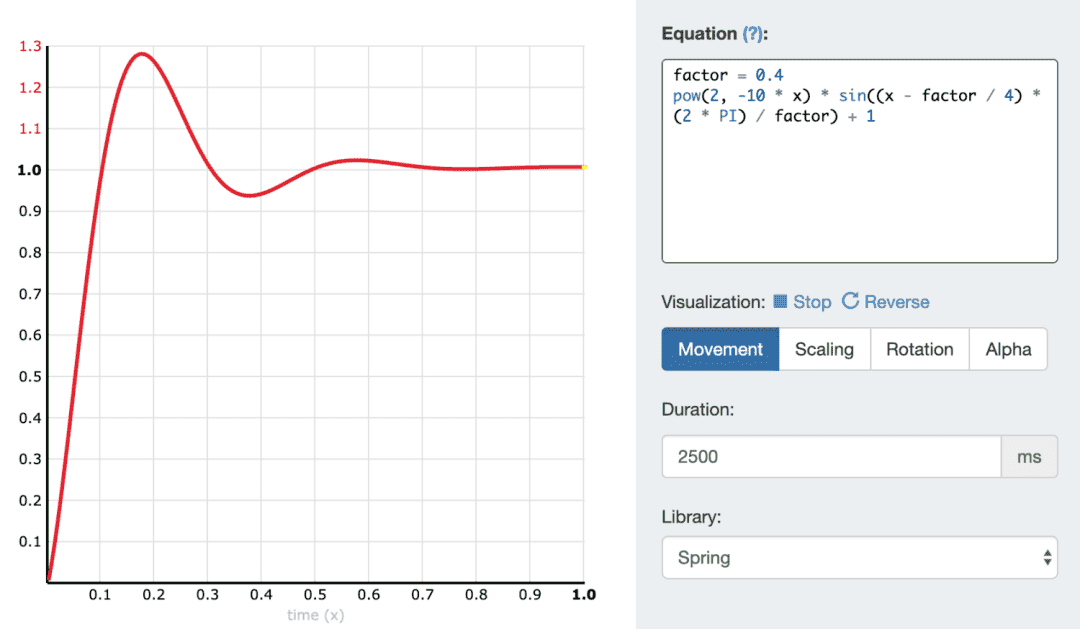
呼吸动画:

三、互联网动效设计的物理法则——运动动画的设计理念
运动动画和动效设计是本质相通的,我们需要为用户建立一种“视觉的真实”,即动作是可信的;我们需要获得的不是照搬线下场景的写实主义,而是“可信度”,要让用户感知到这个动作是成立的。
物理学四大基本力——万有引力、电磁相互作用力、弱相互作用力、强相互作用力,我们在现实生活中能够感知到的基本上都源自万有引力(其他三种力咱也分析不出来啥)。
换句话说,用户在现实生活中建立的动作经验,皆源于物体的“重量感”。
1. 牛顿第一定律
根据牛顿第一定律——惯性定律,任何物体都要保持匀速直线运动或静止状态,直到外力迫使它改变运动状态为止;就是不考虑任何力的作用的物体运动,其速度大小和方向是没有任何变化的,用公式表示:

通过以上公式我们可以绘制出匀速直线运动的位移-时间曲线:

应用到网页设计中,为了实现过渡效果,我们必须模拟出页面区块的位移-时间曲线,对于运动拆解分析得到的分段曲线,可以运用计算机图形图像造型的基本工具——贝塞尔曲线绘制出来,调用CSS3 animation-timing-function 属性中的贝塞尔曲线绘制函数cubic-bezier可以轻松的用程序模拟运动轨迹。
对于匀速直线运动,将运动时间设置为1s,通过cubic-bezier(0,0,1,1)模拟运动如下:

linear 动画从头到尾的速度是相同的。
应用到网页的banner区域切换动效中的效果(动图需加载):

感觉不是很自然,由于空气阻力的存在,程序模拟的匀速直线运动在现实生活中是很难实现的;因此对于这样一个用户平时很少感知到的运动是很难建立信任感的。
这样的匀速直线运动也是我们在进行动效设计时需要极力避免的,考虑到需要分析物体运动的受力情况,我们借助牛顿第二定律来拆解运动。
2. 牛顿第二定律
1)加速运动
根据牛顿第二定律——物体加速度的大小跟作用力成正比,跟物体的质量成反比,加速度的方向跟作用力的方向相同。
当物体持续受到一个不变的力的作用时,它将做匀加速直线运动,用公式表示:

绘制出匀加速直线运动的位移-时间曲线:

通过cubic-bezier(0.42,0,1,1)模拟运动如下:

ease-in 动画从低速开始,逐渐加速,收尾态速度最快。
应用效果:

2)匀减速运动
开始状态符合静止物体开始运动的物理规律,但是收尾态不太符合,物体在结束运动之前速度是整个运动过程中最快的,这是不合逻辑的。
如果我们让收尾状态符合物理法则,那么就是需要让物体减速下来,匀减速运动的公式如下:

绘制出匀加速直线运动的位移-时间曲线:

通过cubic-bezier模拟运动如下:

ease-out 动画从高速开始,以低速结束。
应用效果:

模拟的是物体收到一个持续时间很短的推力作用后自然滑行并慢慢停止的过程,在本应用场景使用这种效果是比较合适的;banner图片刚开始切换运动时,需要用一个比较快的速度来吸引用户的注意力“嗨!这儿有新的信息!”
在快要抵达最终位置的时候,需要逐渐慢下来,因为此时用户已经将注意力转移到新的banner图上了,用户需要的是这一区块逐渐慢下来好看清楚上面的内容,获取信息。
3)缓入缓出
如果想要让banner图片在起始阶段也是柔和地出现,可以缓入缓出一起使用,位移-时间曲线:

通过cubic-bezier(0.42,0,0.58,1)模拟运动如下:

ease-in-out 动画从低速开始,以低速结束。
应用效果:

切换效果非常的柔和,也就是我们常说的“缓入缓出”。
3. 赋予材质——速度、形变和反馈
好的动效在满足了基本的物理原则之后还有很多“材质”上的细节补充,主要有速度、形变和反馈这三个方面。
如果我们想要给上面的案例加上一点重量感,也就是让物体看上去“有质量”,可以再速度上做一点文章,调节一下运动曲线。

通过cubic-bezier(0.25,0.1,0.25,1)模拟运动:

ease动画从低速开始,动画以低速开始,然后加快,在结束前变慢。
应用效果:

我们可以用这种开始态和结束态绝对值不等的加速度让运动产生“粘滞感”,可以让运动的区块产生更加真实的互动效果;但是另一方面,不对等的加速和减速过程有可能会让动效产生拖泥带水、不干脆的感觉,具体应用还是要具体情况具体分析。
做到对物体运动过程的拆解分析再程序模拟之后,我们还可以对运动物体的形状上花一些小心思,通过物体形变和运动的反馈效果可以为物体赋予“材质”。
四、运动动画的设计流程
对于基本动效的其他动作,如缩放、旋转、不透明度等等效果的变化,其本质上和运动是相通的,结合物理法则的分析实践均可以做出自然流畅的效果。
总结一下应用流程:
- 分析具体内容区块的运动,结合需求本身绘制出区块运动的运动数值——运动时间曲线;确立基础时间单位(ms)。
- 拆解曲线,运用贝塞尔曲线模拟运动。
- 通过速度调整、材质形状变化和运动反馈来为区块赋予动效丰富的细节。
作者:JingwhaleDesign,公众号:JingwhaleDesign
原文地址:https://mp.weixin.qq.com/s/d1IdYQ3-teargfXmHm7DIQ
本文作者 @JingwhaleDesign
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
