「深度」AB测试中的因果推断——随机化分流

上一篇文章“「深度」A/B测试中的因果推断——潜在结果模型”中我们介绍了用于A/B测试因果推断的潜在结果模型，现在我们来看看在统计推断中如何应用这个模型，对试验的因果效果进行估计。

一、分流机制

前面我们说过，对于因果效果的估计，我们需要比较多个个体的实际观测到的潜在结果，其中一部分个体和另外一部分分别接受不同的处理，观测到不同的潜在结果。

假如我们有两个用户参与这个雾霾小试验：小强和小明，观测到如下的结果。

表面上来看，小强不戴口罩咳嗽 100 分钟，小明戴口罩也是咳嗽 100 分钟，我们也许就简单地得出一个结论：雾霾时戴口罩没有用，咳嗽不会少。

但是真实情况可能是：小强对雾霾的抵抗力比小明好很多，所以他不戴口罩咳嗽 100 分钟，戴口罩只咳嗽 10 分钟；而身体较弱的小明不戴口罩会咳嗽 200 分钟，戴口罩咳嗽 100 分钟。

那么真实的因果效果应该是戴口罩少咳嗽 100 分钟左右，我们从数据表面得出的戴口罩无用的结论是错误的。

上面给出的是一个只有两个个体的简单例子，如果参与试验的个体很多，同样可能出现这样的状况。

1. 问题出在哪里？

显然，个体之间是存在差异的，如果我们把抵抗力强的分派在一组，把抵抗力差的分派到另外一组，然后进行对比，结果就会和真实情况偏差很大，从而得出错误的结论。

问题的关键在于参与试验的用户进行分组的方法，也就是哪些用户观测到戴口罩的潜在结果，哪些用户观测到不戴口罩的潜在结果，这是对试验比较的结果影响很大的重要因素。

我们把这个分组的过程称为用户分流/分派机制 (assignment mechanism)。

也就是说，多个个体参与试验并不足以保证我们进行有效的因果推断，我们必须掌握个体的分流机制这个关键信息或者对其进行有计划的控制。

分流机制和因果效果的定义没有关系，但是它是潜在结果模型应用过程中的关键一步，是决定效果估计准确性的重要因素。

我们通常需要在试验设计中选择一个好的分流方案，以使得因果效果的估计接近于它的定义，并且尽可能提升试验的统计功效。

因果效果是通过潜在结果（只能观测到其中一个）的比较来定义的，和实际接受到的处理无关。

但是，因为我们只能观测到一半的潜在结果，无法得知个体的因果效果，在评估因果效果时就存在一个因果推断的困难：数据缺失问题，个体没有接受到的处理所对应的潜在结果的数据是缺失的。

因此，解决问题的关键就是缺失数据的处理机制，在因果推断中就是分流机制。

哪些个体应该接受哪些处理，或者说哪些潜在结果应该被观测到？分流机制的这些分派决定是非常关键的。

我们再看看有 4 个用户参与雾霾小试验的例子，这次试验增加了用户小芳和小刚，小芳和小强在一组，不戴口罩；小刚和小明在一组，戴口罩。

观测到数据如下：

这次从数据上看：不戴口罩咳嗽 150 分钟（平均）、戴口罩咳嗽 55 分钟（平均）、结论是戴口罩可以减少咳嗽时间 95 分钟（平均）。

和真实的个体因果效果对比我们可以看出，这个估计结果是很准确的。

这次试验为什么可以推断出正确的结论呢？

因为我们增加了试验用户小芳和小刚，而小芳的雾霾抵抗力和小明接近（相同），小刚的抵抗力和小强接近（相同）；

从而解决了数据缺失的问题：你可以把小芳的结果看作是小明没有观测到的不戴口罩情况下的潜在结果，把小刚的结果看作是小强没有观测到的戴口罩情况下的潜在结果。

这里分流的关键在于把用户属性（抵抗力）差不多的小强 vs 小刚，以及小明 vs 小芳，分派到两个不同的组，接受不同的处理。

如果反过来，把属性差不多的用户都放在同一个组，那么数据缺失问题还是没有得到解决，试验结论和上面两个用户情况下的试验一样依然是错的。

从这两个例子我们可以看出：我们不能脱离个体的分流机制而仅仅由个体观测到的潜在结果来进行因果推断。

有效的推断要求我们必须考虑这个问题：为什么这些用户接受这个处理，另外的用户接受另一个处理？

二、随机化试验

采用随机化分流方式的试验设计就是随机化试验 (Randomized Experiments)，它是我们在 A/B 测试中进行统计推断的基础。传统的随机化试验主要有三种类型：

1. 伯努利（Bernoulli）随机化试验
2. 完全随机化试验（Completely Randomized Experiments）
3. 分层随机化试验（Stratified Randomized Experiments）

最简单的 Bernoulli 试验以类似于抛硬币的方式来决定每一个个体的分派；

完全随机化试验中每个 treatment 分派到的个体数量是固定的，但个体的分派是随机的；分层随机化则是在完全随机化的基础上，先通过协变量对总体进行分层，然后在层内随机化分派。

不同的随机化试验类型（随机化分流方式）导致不同的分派概率分布。

以完全随机化试验为例，其个体概率如下：

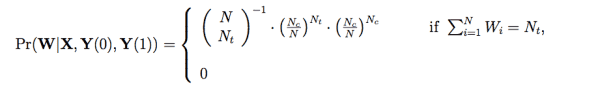
根据这个概率分布，我们就可以对总体的平均因果效果进行统计推断和估计了。

平均因果效果的估计

让我们先从数学上正式地定义平均因果效果（Average Causal Effect），它是我们试验和分析的最终目标。

首先把总体中所有的个体编号为 i = 1, …, N，N 是总体的容量。

每个个体可接受一组处理中的一个，我们用 Ti 来表示个体 i 可接受的处理的集合。

大多数情况下，这个集合对所有个体都是相同的。

在我们的小试验中，Ti 包括两个处理水平：0 表示不戴口罩（control 组），1 表示戴口罩（treatment 组）。

每个个体可接受的处理水平都有一个对应的潜在效果，Yi（0）和 Yi（1）、Yi（1）和 Yi（0） 的比较（通常是差值），就是个体 i 的因果效果了。

个体的因果效果我们是无法直接得知的，也不是我们的关注重点。

我们通常关心的是总体中所有个体的因果效果的平均值，即平均因果效果。

其中

分别是所有个体不戴口罩（0）的平均潜在结果，和所有个体戴口罩（1）的平均潜在结果。

ACE 就是我们试验分析的目标，它等于“戴口罩（1）的平均潜在结果 ——不戴口罩（0）的平均潜在结果”。

我们前面已经说过，每个个体的两个潜在结果只能观测到其中一个，另外一个是不知道的，所以Yi（0）和Yi（1） 里面有一半是没有观测值的，我们不能由 ACE 的定义公式直接计算出它的值。

对 ACE 的一个很自然的估计量就是“treatment 组观测到的平均潜在结果—control 组观测到的平均潜在结果”

假设参与试验的 N 个用户中有 Nt 个分派到 treatment 组，Nc 个在 control 组，那么 treatment 组和 control 组的平均潜在结果分别是

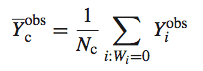
我们需要评估一下这个估计量的准确性，最基本的衡量标准就是它是否 ACE 的无偏估计，即该估计量的期望是否等于 ACE。

令指示变量 Wi 表示个体 i 被分派的处理（取值 0 或 1），估计量可改写为：

其期望值：

如果分派机制 W 是完全随机化分派，那么随机变量 Wi 的期望：

因此可得：

可知，在完全随机化试验中，我们根据直观得到的简单估计量是 ACE 的无偏估计，是基本可用的。

从上面的推断过程可以看出，个体的完全随机化分派机制在其中扮演了非常重要的角色，正是由于随机变量 Wi 的概率分布的特点，使得 ACE 的这个简单估计量是无偏估计。

现在我们来看看这个 ACE 估计量的精确性，也就是其抽样方差。

根据随机变量 Wi 的概率分布的特点，通过类似的方法，可得到 ACE 估计量的方差为：

其中

分别是潜在结果 Yi（0）和 Yi（1）的样本方差，而

则是个体因果效果 Yi(1) – Yi(0) 的样本方差。

如果总体中的个体因果效果为常量（例如，戴口罩的效果对所有人都是少咳嗽 100 分钟），那么该项为 0，我们得到：

以观测到的组内样本方差近似代替总体的样本方差可得到一个方差估计量：

结合平均因果效果的估计量和抽样方差估计量可得到假设检验统计量为：

是不是看起来很眼熟？嗯，其实就是我们常用的独立双样本情况下的 z 检验量的计算公式：

大家现在是不是对隐藏在这个公式里的因果效果有所理解了？！

作者：祁永辉，微信：yonghuishuo，微信公众号：AB试验，热云数据AB测试事业部增长顾问，专注于AB试验（A/Btest）相关知识分享

本文作者 @祁永辉

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！