支持向量机：分类算法中的“战斗鸡”

上篇文章我们介绍了决策树和随机森林算法，接下来让我们用掌声隆重欢迎分类算法中的“战斗鸡”：支持向量机。

大家可能都听过这个一句话：你考99分是因为你只能考到99分，而学霸考100分是因为试卷只有100分。

用学霸来形容支持向量机（Support Vector Machine，SVM）算法其实一点都不过分，因为它可以说是机器学习分类算法中的“天花板”战力了。

SVM算法不仅模型效果好，而且思维逻辑超前，所以即便是在深度学习横行的今天，也因为比深度神经网络更轻量级，而被作为模型效果的基准线。

一、基本原理

举个栗子，我们要把下图中的蓝圈圈和红方块用一条线分开，会发现可以画出无数条线，并且这些线都非常好的完成了任务，看起来好像没什么差别。

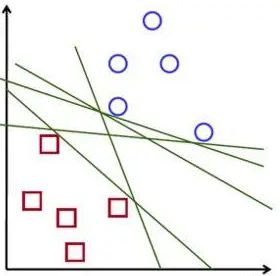
接下来，我们又加上了两个绿色的三角形（新样本），上方的三角形更靠近蓝圈圈，下方的三角形更靠近红方块。根据之前介绍的K近邻算法的原理，距离越近的样本表示越相似，我们可以得到结论：上方的三角形大概率属于蓝圈圈，下方的三角形大概率属于红方块。

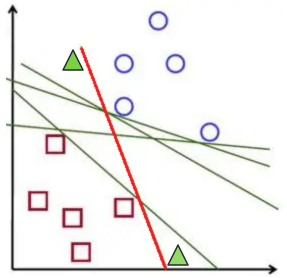
那我们再来看刚才表现“完美”的那几条线，会发现这条红线表现出现了问题，分类和预期不一致，表现不如其他线。

这说明我们在确定分类线的时候，不仅要保证分类的正确性，还要尽可能保证边界样本点到这条线的距离尽可能远，以留出足够多的安全边际。而距离线越远，表示区分度越高，分类效果越好。

按照这个思路，我们可以找到下图的这条分类线，它是距离两个类别间隔最大的线，也可以称为两类样本数据之间的中轴线。

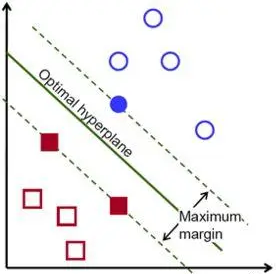
刚才描述的思路就是支持向量机（SVM）的基本思路：当样本数据是线性可分的时候，找出距离两类样本间隔最大的一条线，这条线不止保证了分类的正确性，还尽可能让两个类别更容易区分。

图中实心的蓝圈圈和红方块，是距离这条线最近的样本点，就叫做支持向量（Support Vector），这几个边界点到这条线的距离称为间隔。

间隔距离越大，分类效果的安全边际越高，就算有新数据超出了原有样本的边界，但只要差距没超过间隔，分类结果就不会受影响，而寻找最大间隔的过程就是SVM算法最优化参数的过程。

刚才举的栗子是基于线性可分的样本数据，那么面对下图中的非线性可分的样本，SVM是怎么处理的呢？

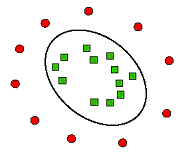
SVM的解决思路就是升维，将二维平面映射到三维空间，刚才那条分类线在三维空间上的投影就变成了一个平面，这个平面把原有的空间分割成两部分，让二维空间中混杂的样本在三维空间中线性可分。

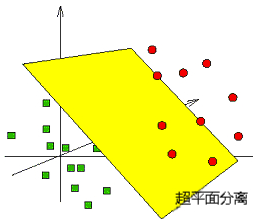
我们按照这个思路继续外推，比如映射到一个更高维的空间，依然可以找到使样本线性可分的那条“线”，只不过这条“线”是一个超平面。

SVM通过“核函数”来将样本从低维空间映射到高维空间，让样本数据在新空间中线性可分。常见的核函数有线性核函数、多项式核函数、高斯核函数等。

所以，SVM就是一个有监督的二分类器，目标是找到一个超平面，让两类数据距离这个超平面最远，从而对新样本数据的分类更准确。

二、应用场景

SVM不仅适用于线性问题，还适用于非线性问题，具有较好的分类性能和泛化能力，适用于多种实际问题的解决。

• 文本分类：SVM可以将文本表示为特征向量，并通过训练一个SVM分类器来将文本分为不同的类别，如垃圾邮件分类、情感分析、文本主题分类等。
• 图像分类：通过提取图像的特征向量，可以使用SVM来训练一个分类器，将图像分为不同的类别，如人脸识别、物体识别、图像检索等。
• 生物医学领域：可以使用SVM来进行癌症分类、蛋白质结构预测、基因表达数据分析等。
• 金融领域：SVM可以用于金融领域的多个任务，如信用评分、欺诈检测、股票市场预测等。
• 医学图像分析：可以使用SVM来进行病变检测、疾病诊断、医学图像分割等。
• 自然语言处理：可以使用SVM进行命名实体识别、句法分析、机器翻译等任务。

三、优缺点

SVM算法的优点：

• 高准确性：SVM在处理二分类问题时具有较高的准确性，尤其在小样本数据集上表现出色。
• 泛化能力强：SVM通过最大化间隔来提高模型的泛化能力，减少过拟合的风险。
• 可处理高维数据：SVM在高维数据上的表现较好，因为在高维空间中，数据更容易线性可分。
• 非线性问题处理：通过使用核函数，SVM可以处理非线性问题，将数据映射到高维空间，从而提高分类的准确性。
• 特征选择：SVM可以通过支持向量的重要性来进行特征选择，帮助识别最重要的特征，减少特征维度。
• 对异常值的鲁棒性：SVM对于异常值具有较好的鲁棒性，不容易受到异常值的影响。

SVM算法的缺点：

• 计算复杂度高：SVM在处理大规模数据集时的计算复杂度较高，需要较长的训练时间和较大的内存消耗。
• 参数选择敏感：SVM的性能受到参数选择的影响，如核函数的选择、正则化参数的选择等，需要进行调优。
• 不适用于大规模数据集：由于计算复杂度高，SVM在处理大规模数据集时可能不太适用。
• 不适用于噪声较多的数据集：SVM对于噪声较多的数据集敏感，可能会导致模型的性能下降。
• 不直接提供概率估计：SVM本身不直接提供概率估计，需要通过一些额外的方法来进行概率估计。

四、总结

本文我们介绍了支持向量机（SVM）的原理、应用场景和优缺点，希望对大家有所帮助。

下篇文章，我们来聊一聊解决聚类问题的K均值算法，敬请期待。

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！