K均值聚类算法

一、什么叫K均值聚类算法？

K均值聚类算法也叫K-means聚类算法，是一种无监督学习算法。

二、基本原理

假设有一个新开办的大学，即便还没有开设任何的社团，有不同兴趣爱好的同学们依然会不自觉的很快聚在一起，比如喜欢打篮球的、喜欢打乒乓球的、喜欢音乐的等等。

这时候就可以顺势开设篮球社团、乒乓球社团、音乐社团，再有同学想加入社团的时候，就可以直接根据自身兴趣选择社团了。

把这个场景迁移到机器学习上，拥有不同兴趣的学生就是数据样本，我们来试着来给他们归类。

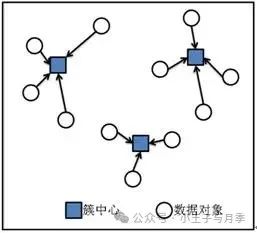
向量空间中，距离近的样本意味着有更高的相似度，我们就把它们归为一类，然后用该类型所有样本的中心位置标识这个类别，再有新样本进来的时候，新样本离哪个类别的中心点更近，就属于哪个类别，然后再重新计算确定新的中心点。

不断重复上述操作，就能把所有的数据样本分成一个个无交集的簇，也就是对所有数据样本完成了归类。

这就是K-means算法的思路及原理：将数据集划分为K个不重叠的独立聚类，再找出这个K个类别的中心位置，新的样本离中心位置最近则归属哪个类别。

这里生成的新簇中，需重新计算每个簇的中心点，然后在重新进行划分，直到每次划分的结果保持不变。在实际应用中往往经过很多次迭代仍然达不到每次划分结果保持不变，甚至因为数据的关系，根本就达不到这个终止条件，实际应用中往往采用变通的方法设置一个最大迭代次数，当达到最大迭代次数时，终止计算。

需要注意的是，K-means算法中的K表示要分成K个聚类，那么如何确定K值就是一个绕不开的问题了。其实没有统一的标准，这里一般两种办法：

1、我们一般根据个人经验来设定K值（可用观察法看粗略地看有多少簇）。

2、尝试每一个K值，然后在不同的K值情况下，通过每个待测点到质心的距离之和，来计算平均距离。着K值的变化，最终会找到一个点，让平均距离变化放缓，这个时候基本就可以确定K值了。

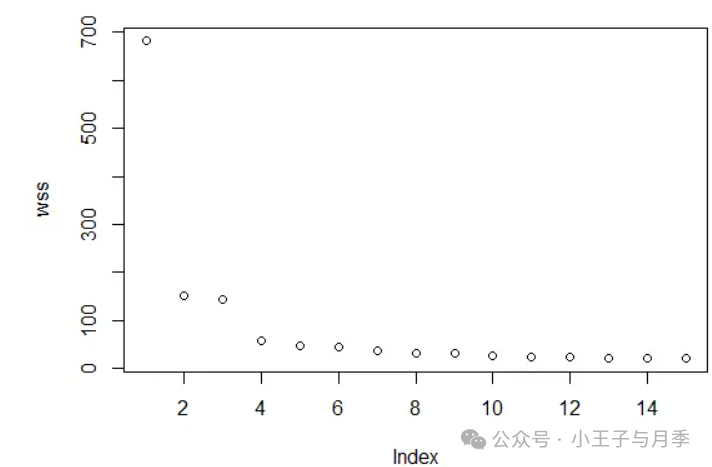
如下图划分数在4-15之间，簇内间距变化很小，基本上是水平直线，因此可以选择K=4（拐点附近位置）作为划分数。

K-Means算法涉及到簇中心的计算，对于第i个簇，其簇中心（质心）的计算公式为：

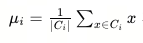
K均值聚类的目标是最小化簇内平方误差，即找到K个簇，使每个数据点与其所属簇中心的距离之和最小。目标函数的数学公式是：

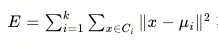
从公式可见，E值越小则簇内数据（样本）相似度越高。K-Means算法通过迭代更新簇中心，不断优化这个目标函数，来达到更好的聚类效果。

三、K均值聚类算法的步骤是什么？

1. 初始化：随机选择K个数据点作为初始簇中心。
2. 分配数据点：对于数据集中的每个数据点，计算其与各个簇中心的距离，并将其分配到距离最近的簇中心所在的簇。
3. 更新簇中心：计算每个簇内所有数据点的均值（或其它形式的中心），将其作为新的簇中心。这个均值可以是算术平均值、几何平均值、中位数等。
4. 重新计算误差：重新计算每个簇内数据点到簇中心的距离，并计算总的平方误差。
5. 迭代：重复步骤(2)—(4)，直到满足停止条件。停止条件可以是簇中心的变化小于某个阈值，或是达到预设的最大迭代次数，又或是误差函数的减少小于某个值。

四、应用场景

K均值聚类算法，可以帮我们完成大量数据的分类任务。

商业务中，精细化运营的前提是对用户进行分层，然后根据不同层次的用户采取不同的运营策略。这时候可以收集用户的消费频率、消费金额、最近消费时间等消费数据，并使用K-means算法将用户分为不同的层级，然后针对高价值用户，可以提供专享活动或个性化服务，提高用户价值感和忠诚度，针对将要流失的用户，可以采用发放优惠券等挽留策略，尽可能留住用户。

以下是一些更多应用场景：

1. 文档聚类：在自然语言处理中，可用于文档聚类，将相似的文档分为同一类，以便进行更有效的信息检索。
2. 客户细分：在市场营销中，可对客户进行细分，将相似的客户分为同一类，以便进行更有效的营销策略制定。
3. 图像分割：在计算机视觉中，可用于图像分割，将图像中的像素分为几个不同的区域。
4. 异常检测：可用于异常检测，通过将数据点聚类，找出那些与大多数数据点不同的异常数据点。
5. 社交网络分析：在社交网络分析中，K-means可用于发现社区结构，将相似的用户分为同一类。

五、优缺点

K-means算法的优点：

1. 简单易实现：原理简单，实现起来相对容易。
2. 计算效率高：时间复杂度近似为线性，对于大规模数据集可以较快地得到结果。
3. 可解释性强：结果（即聚类中心）具有很好的可解释性。
4. 收敛速度快：在大多数情况下，K-means算法能够较快速地收敛到局部最优解。
5. 优化迭代功能：可以在已经求得的聚类基础上进行迭代修正，提高聚类的准确性。

K-means算法的缺点：

1. 准确度上比不上有监督学习的算法
2. 对噪声和离群点敏感：对噪声和离群点敏感，这些点可能会影响聚类中心的计算。
3. 需要预设聚类数目：需要预先设定K值（即聚类的数目），但这个值通常难以准确估计。
4. 对初始值敏感：算法结果可能会受到初始聚类中心选择的影响，不同的初始值可能会导致不同的聚类结果。
5. 可能收敛到局部最优：可能会收敛到局部最优解，而非全局最优解。

参考文档：

2、K-means聚类算法：用“物以类聚”的思路挖掘高价值用户

作者：厚谦，公众号：小王子与月季

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！