视觉注意力机制(上)

简介

注意力机制（Attention Mechanism）是机器学习中的一种数据处理方法，起源于自然语言处理（NLP）领域，后来在计算机视觉中广泛应用。注意力机制本质上与人类对事物的观察机制相似：一般而言，我们在观察事物的时候，首先会倾向于观察事物一些重要的局部信息（如下图所示，我们会首先将注意力集中在目标而不是背景的身上），然后再去关心一些其他部分的信息，最后组合起来形成整体印象。

注意力机制能够使得深度学习在提取目标的特征时更加具有针对性，使得相关任务的精度有所提升。注意力机制应用于深度学习通常是对输入每个部分赋予不同的权重，抽取出更加关键及重要的信息使模型做出更加准确的判断，同时不会对模型的计算和存储带来更大的开销，这也是注意力机制广泛使用的原因。

在计算机视觉中，注意力机制主要和卷积神经网络进行结合，按照传统注意力的划分，大部分属于软注意力，实现手段常常是通过掩码（mask）来生成注意力结果。掩码的原理在于通过另一层新的权重，将输入特征图中关键的特征标识出来，通过学习训练，让深度神经网络学到每一张新图片中需要关注的区域，也就形成了注意力。说的更简单一些，网络除了原本的特征图学习之外，还要学会通过特征图提取权重分布，对原本的特征图不同通道或者空间位置加权。因此，按照加权的位置或者维度不同，将注意力分为空间域、通道域和混合域。

典型方法

卷积神经网络中常用的注意力有两种，即空间注意力和通道注意力，当然也有融合两者的混合注意力，画了个示意图如下。

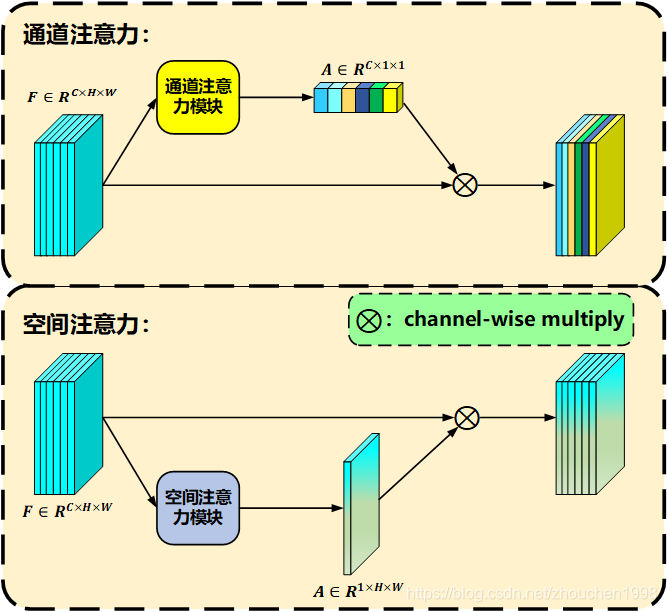
首先，我们知道，卷积神经网络输出的是维度为$C\times H\times W$的特征图，其中$C$指的是通道数，它等于作用与输入的卷积核数目，每个卷积核代表提取一种特征，所以每个通道代表一种特征构成的矩阵。$H\times W$这两个维度很好理解，这是一个平面，里面的每个值代表一个位置的信息，尽管经过下采样这个位置已经不是原始输入图像的像素位置了，但是依然是一种位置信息。如果，对每个通道的所有位置的值都乘上一个权重值，那么总共需要$C$个值，构成的就是一个$C$维向量，将这个$C$维向量作用于特征图的通道维度，这就叫通道注意力。同样的，如果我学习一个$H\times W$的权重矩阵，这个矩阵每一个元素作用于特征图上所有通道的对应位置元素进行乘法，不就相当于对空间位置加权了吗，这就叫做空间注意力。

下面我列举一些常见的使用了注意力机制的卷积神经网络，我在下面一节会详细介绍它们。

1. NL(Non-local Neural Networks)
2. SENet(Squeeze-and-Excitation Networks)
3. BAM(Bottleneck Attention Module)
4. CBAM(Convolutional Block Attention Module)
5. A2A^2A2-Nets(Double Attention Networks)
6. GSoP-Net(Global Second-order Pooling Convolutional Networks)
7. GCNet(Non-local Networks Meet Squeeze-Excitation Networks and Beyond)
8. ECA-Net(Efficient Channel Attention for Deep Convolutional Neural Networks)
9. SKNet(Selective Kernel Networks)
10. CCNet(Criss-Cross Attention for Semantic Segmentation)
11. ResNeSt(ResNeSt: Split-Attention Networks)
12. Triplet Attention(Convolutional Triplet Attention Module)

网络详解

NL

Non-local Neural Networks 应该算是引入自注意力机制比较早期的工作，后来的语义分割里各种自注意力机制都可以认为是 Non-local 的特例，这篇文章作者中同样有熟悉的何恺明大神 😂。

首先聊聊 Non-local 的动机，我们知道，CV 和 NLP 任务都需要捕获长程依赖（远距离信息交互），卷积本身是一种局部算子，CNN 中一般通过堆叠多层卷积层获得更大感受野来捕获这种长程依赖的，这存在一些严重的问题：效率低；深层网络的设计比较困难；较远位置的消息传递，局部操作是很困难的。所以，收到非局部均值滤波的启发，作者设计了一个泛化、简单、可直接嵌入主流网络的 non-local 算子，它可以捕获时间（一维时序数据）、空间（图像）和时空（视频）的长程依赖。

首先，Non-local 操作早在图像处理中已经存在，典型代表就是非局部均值滤波，到了深度学习时代，在计算机视觉中，这种通过关注特征图中所有位置并在嵌入空间中取其加权平均值来计算某位置处的响应的方法，就叫做自注意力。

然后来看看深度神经网络中的 non-local 操作如何定义，也就是下面这个式子，这是一个通式，其中$x$是输入，$y$是输出，$i$和$j$代表输入的某个位置，可以是序列、图像或者视频上的位置，不过因为我比较熟悉图像，所以后文的叙述都以图像为例。因此xix_ixi​是一个向量，维数和通道一样；$f$是一个计算任意两点的相似性函数，$g$是一个一元函数，用于信息变换；$\mathcal{C}$是归一化函数，保证变换前后整体信息不变。所以，下面的式子，其实就是为了计算某个位置的值，需要考虑当前这个位置的值和所有位置的值的关系，然后利用这种获得的类似 attention 的关系对所有位置加权求和得到当前位置的值。

yi=1C(x)∑∀jf(xi,xj)g(xj)\mathbf{y}_{i}=\frac{1}{\mathcal{C}(\mathbf{x})} \sum_{\forall j} f\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right) g\left(\mathbf{x}_{j}\right) yi​=C(x)1​∀j∑​f(xi​,xj​)g(xj​)

那么，确定了这个通式，在图像上应用，只需要确定$f$、$g$和$\mathcal{C}$即可，首先，由于$g$的输入是一元的，可以简单将$g$设置为 1x1 卷积，代表线性嵌入，算式为g(xj)=Wgxjg\left(\mathbf{x}_{j}\right)=W_{g} \mathbf{x}_{j}g(xj​)=Wg​xj​。关于$f$和$\mathcal{C}$需要配对使用，作用其实就是计算两个位置的相关性，可选的函数有很多，具体如下。

• Gaussian
  高斯函数，两个位置矩阵乘法然后指数映射，放大差异。
  f(xi,xj)=exiTxjf\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=e^{\mathbf{x}_{i}^{T} \mathbf{x}_{j}} f(xi​,xj​)=exiT​xj​
  C(x)=∑∀jf(xi,xj)\mathcal{C}(x)=\sum_{\forall j} f\left(\mathrm{x}_{i}, \mathrm{x}_{j}\right) C(x)=∀j∑​f(xi​,xj​)
• Embedded Gaussian
  嵌入空间的高斯高斯形式，$\mathcal{C}(x)$同上。
  θ(xi)=Wθxiand ϕ(xj)=Wϕxj\theta\left(\mathbf{x}_{i}\right)=W_{\theta} \mathbf{x}_{i} \text { and } \phi\left(\mathbf{x}_{j}\right)=W_{\phi} \mathbf{x}_{j} θ(xi​)=Wθ​xi​ and ϕ(xj​)=Wϕ​xj​
  f(xi,xj)=eθ(xi)Tϕ(xj)f\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=e^{\theta\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right)} f(xi​,xj​)=eθ(xi​)Tϕ(xj​)
  论文中这里还特别提了一下，如果将$\mathcal{C}(x)$考虑进去，对1C(x)f(xi,xj)\frac{1}{\mathcal{C}(\mathbf{x})} f\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)C(x)1​f(xi​,xj​)而言，这其实是一个 softmax 计算，因此有y=softmax⁡(xTWθTWϕx)g(x)\mathbf{y}=\operatorname{softmax}\left(\mathbf{x}^{T} W_{\theta}^{T} W_{\phi} \mathbf{x}\right) g(\mathbf{x})y=softmax(xTWθT​Wϕ​x)g(x)，这个其实就是 NLP 中常用的自注意力，因此这里说，自注意力是 Non-local 的特殊形式，Non-local 将自注意力拓展到了图像和视频等高维数据上。但是，softmax 这种注意力形式不是必要的，因此作者设计了下面的两个 non-local 操作。
• Dot product
  这里去掉了指数函数形式，$\mathcal{C}(x)$的形式也相应改变为$x$上的像素数目。
  f(xi,xj)=θ(xi)Tϕ(xj)f\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\theta\left(\mathbf{x}_{i}\right)^{T} \phi\left(\mathbf{x}_{j}\right) f(xi​,xj​)=θ(xi​)Tϕ(xj​)
  $$\mathcal{C}(\mathbf{x})=N$$
• Concatenation
  最后，是一种 concat 的形式，$[\cdot ,\cdot ]$表示 concat 操作，$\mathcal{C}(x)$同上。
  f(xi,xj)=ReLU⁡(wfT[θ(xi),ϕ(xj)])f\left(\mathbf{x}_{i}, \mathbf{x}_{j}\right)=\operatorname{ReLU}\left(\mathbf{w}_{f}^{T}\left[\theta\left(\mathbf{x}_{i}\right), \phi\left(\mathbf{x}_{j}\right)\right]\right) f(xi​,xj​)=ReLU(wfT​[θ(xi​),ϕ(xj​)])

有了上面定义的 non-local 算子，就可以定义non-local 模块了，其定义如下，其中的+xi+\mathbf{x}_{i}+xi​表示残差连接，这种残差形式可以保证该模块可以嵌入预训练模型中，只要将WzW_zWz​初始化为 0 即可。其实这中间的实现都是通过 1x1 卷积完成的，因此输出和输入可以控制为同等通道数。

zi=Wzyi+xi\mathbf{z}_{i}=W_{z} \mathbf{y}_{i}+\mathbf{x}_{i} zi​=Wz​yi​+xi​

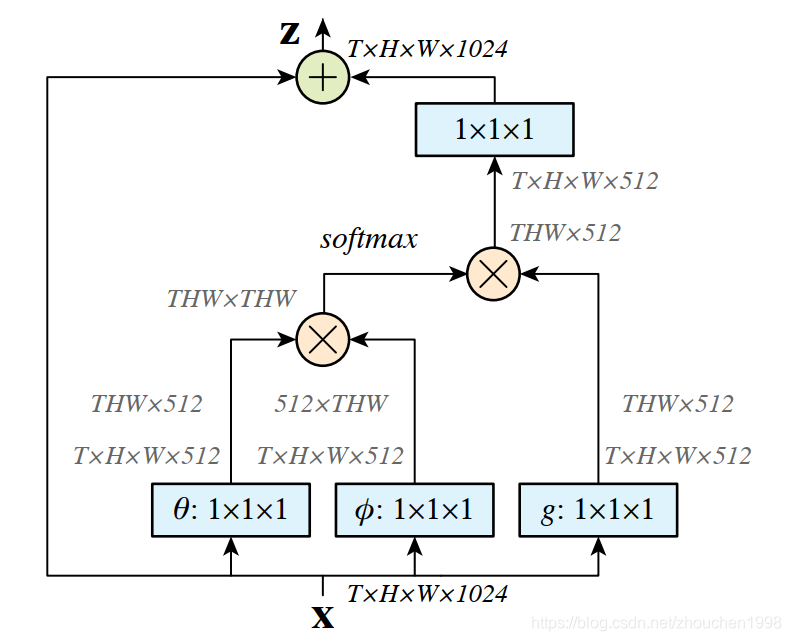
上面是数学上的定义，具体来看，一个时空格式的 non-local 模块如下图，我们从二维图像的角度来看，可以忽略那个$T$，直接将其置为 1 即可。所以，输入是$(h,w,1024)$，经过两个权重变换WθW_\thetaWθ​和WϕW_\phiWϕ​得到降维后的两个特征图，都为$(h,w,512)$，它们两者 reshape 后变为$(h\times w,512)$，之后再其中一个转置后矩阵乘法另一个，得到相似性矩阵$(h\times w,h\times w)$，然后再最后一个维度上进行 softmax 操作。上述这个操作得到一种自注意力图，表示每个像素与其他位置像素的关系。然后将原始输入通过变换$g$得到一个$(h\times w,512)$的输入矩阵，它和刚刚的注意力图矩阵乘法，输出为$(h\times w,512)$，这时，每个位置的输出值其实就是其他位置的加权求和的结果。最后，通过 1x1 卷积来升维恢复通道，保证输入输出同维。

这篇文章有很不错的第三方 Pytorch 实现，想了解更多细节的可以去看看源码和论文，其实实现是很简单的。

最后，简单总结一下这篇文章。提出了 non-local 模块，这是一种自注意力的泛化表达形式，Transformer 的成功已经证明自注意力的长程交互信息捕获能力很强，对网络尤其是处理视频的网络如 I3D 是有参考意义的。当然，其本质还是空间层面的注意力，如果考虑通道注意力或许会获得更好的效果，而且 non-local 模块的矩阵计算开销其实不低，这也制约了 non-local 的广泛应用，略微有点遗憾。

SENet

SENet 应该算是 Non-local 的同期成果，我在之前的文章中专门解读过，这里就大概的说一下。

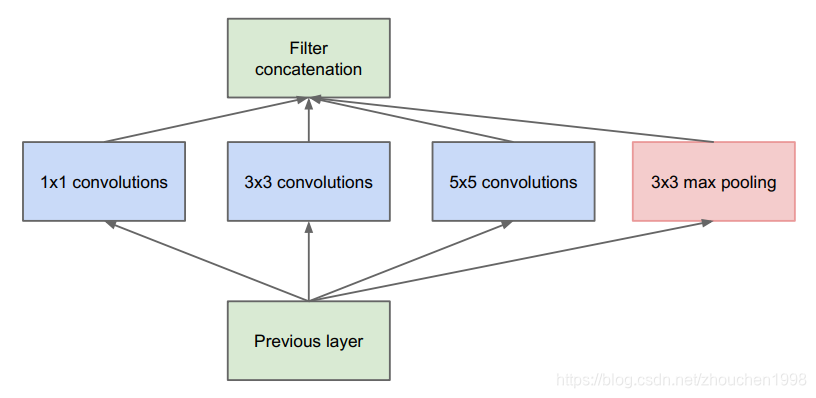
卷积操作是卷积神经网络的核心，卷积可以理解为在一个局部感受野范围内将空间维度信息和特征维度信息进行聚合，聚合的方式是加和操作。然而想要提高卷积神经网络的性能其实是很难的，需要克服很多的难点。为了获得更加丰富的空间信息，很多工作被提出，如下图使用多尺度信息聚合的Inception。

那么，自然会想到，能否在通道维度上进行特征融合呢？其实卷积操作默认是有隐式的通道信息融合的，它对所有通道的特征图进行融合得到输出特征图（这就默认每个通道的特征是同权的），这就是为什么一个32通道的输入特征图，要求输出64通道特征图，需要$32\times 64$个卷积核（这个32也可以理解为卷积核的深度）。通道方面的注意力也不是没人进行尝试，一些轻量级网络使用分组卷积和深度可分离卷积对通道进行分组操作，但这本质上只是为了减少参数，并没有什么特征融合上的贡献。

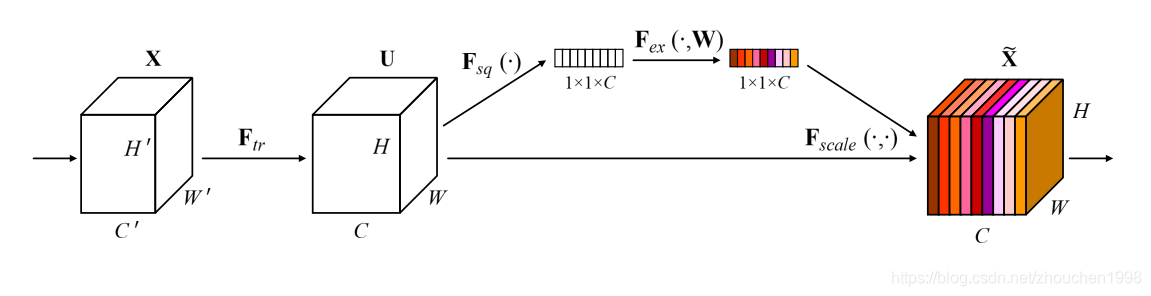
所以，SENet出现了，它从从每个通道的特征图应该不同权的角度出发，更加关注通道之间的关系，让模型学习到不同通道的重要程度从而对其加权，即显式建模不同通道之间的关系。为此，设计了SE（Squeeze-and-Excitation）模块，如下图所示。SE模块的思路很简单，先通过全局平均池化获得每个通道的全局空间表示，再利用这个表示学习到每个通道的重要性权重，这些权重作用与原始特征图的各个通道，得到通道注意力后的特征图。由于轻量简洁，SE模块可以嵌入任何主流的卷积神经网络模型中，因为其可以保证输入输出同维。

BAM

这篇文章和下面的CBAM是同一个团队的成果，非常类似，CBAM收录于ECCV2018，BAM收录于BMVC2018，两篇文章挂到Arxiv上的时间也就差了几分钟而已，这里先简单地说一下区别，BAM其实是通道注意力和空间注意力的并联，CBAM是两者的串联。

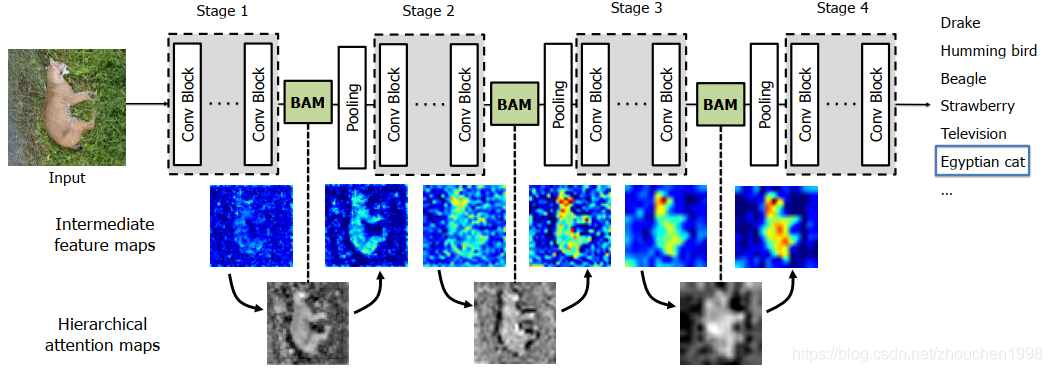
BAM，全名Bottleneck Attention Module，是注意力机制在卷积神经网络中的一次伟大尝试，它提出的BAM模块可以集成到任意的卷积神经网络中，通过channel和spatial两个分支得到注意力图，通道注意力关注语义信息回答what问题，空间注意力关注位置信息，回答where问题，因此结合起来是最好的选择。下图是BAM集成到一个卷积神经网络的示意图，显然，BAM存在于池化层之前，这也是bottleneck的由来，作者说这样的多个BAM模块构建的注意力图层类似人类的感知过程。

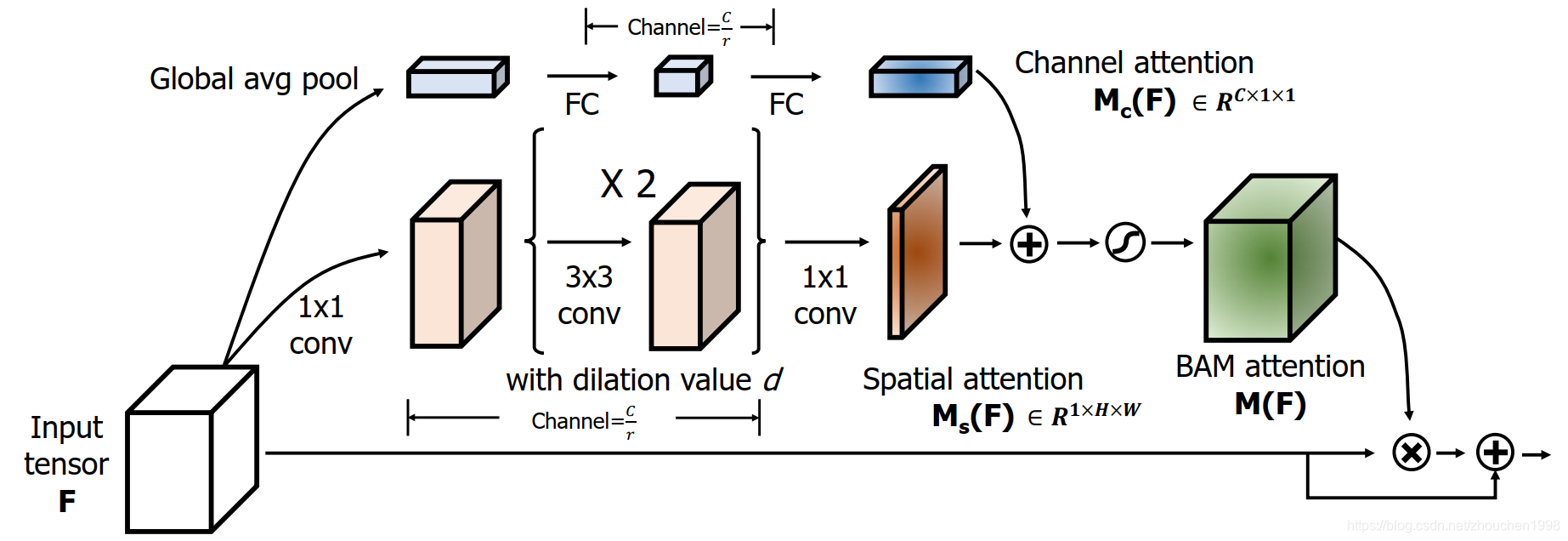
上图就是核心的BAM模块结构图，我们来一步步看它是如何实现通道空间混合注意力的。整体来看，对于输入特征图F∈RC×H×W\mathbf{F} \in \mathbb{R}^{C \times H \times W}F∈RC×H×W，BAM模块最终会得到一个注意力图M(F)∈RC×H×W\mathbf{M}(\mathbf{F}) \in \mathbb{R}^{C \times H \times W}M(F)∈RC×H×W，这里注意到，这是一个和输入同维的张量，此前，通道注意力学习到的是个$C$维向量，空间注意力学到的是个$H\times W$维的矩阵，BAM这种格式表明其混合了通道和空间的注意力信息。 调整后输出的特征图F′=F+F⊗M(F)\mathbf{F}^{\prime}=\mathbf{F}+\mathbf{F} \otimes \mathbf{M}(\mathbf{F})F′=F+F⊗M(F)，显然，这是一个张量点乘后进行加法的运算，加法是明显的残差结构，点乘发生在学到的注意力图和输入特征图之间，因此输出和输入同样shape。为了计算上高效，通道和空间注意力采用并行的分支结构获得。因此，整体计算上要先获得通道注意力图Mc(F)∈RC\mathbf{M}_{\mathbf{c}}(\mathbf{F}) \in \mathbb{R}^{C}Mc​(F)∈RC和空间注意力图Ms(F)∈RH×W\mathbf{M}_{\mathbf{s}}(\mathbf{F}) \in \mathbb{R}^{H \times W}Ms​(F)∈RH×W，上面的最终注意力图通过下式计算得到，其中$\sigma$表示Sigmoid激活函数，两个注意力图的加法需要broadcast，得到的就是$C\times H\times W$维度了。

M(F)=σ(Mc(F)+Ms(F))\mathbf{M}(\mathbf{F})=\sigma\left(\mathbf{M}_{\mathbf{c}}(\mathbf{F})+\mathbf{M}_{\mathbf{s}}(\mathbf{F})\right) M(F)=σ(Mc​(F)+Ms​(F))

然后，我们再来看看具体的两个分支内发生了什么。首先，看通道注意力分支，首先，对输入特征图$\mathbf{F}$进行全集平均池化得到Fc∈RC×1×1\mathbf{F}_{\mathbf{c}} \in \mathbb{R}^{C \times 1 \times 1}Fc​∈RC×1×1，这相当于在每个通道的空间上获得了全局信息。然后，这个向量送入全连接层进行学习，这里进行了一个先降维再升维的操作，所以学到的向量Mc(F)\mathbf{M}_{\mathbf{c}}(\mathbf{F})Mc​(F)依然是$C\times 1\times 1$维度的，这个就是通道注意力图。

接着，我们看看空间注意力分支。作者这里先用1x1卷积对输入特征图降维，然后使用两层膨胀卷积以更大的感受野获得更丰富的信息Ftemp∈RC/r×H×W\mathbf{F_{temp}} \in \mathbb{R}^{C / r \times H \times W}Ftemp​∈RC/r×H×W，最后再用1x1卷积将特征图降维到通道数为1，得到空间注意力图Ms(F)∈RH×W\mathbf{M}_{\mathbf{s}}(\mathbf{F}) \in \mathbb{R}^{H\times W}Ms​(F)∈RH×W。

至此，我们理解了BAM模块的结构，它可以嵌入到主流网络中获得一些性能提升，不过后来并没有在各种任务中获得较好的表现，因此不是很广泛，但它的混合注意力思路是值得借鉴的。

CBAM

CBAM，全名Convolutional Block Attention Module，相对于BAM，在CV中受到了更多的关注，下图就是CBAM的整体结构图，不难发现，它和BAM区别就是通道注意力和空间注意力是串联进行的，实践证明，这样的效果更好一些。

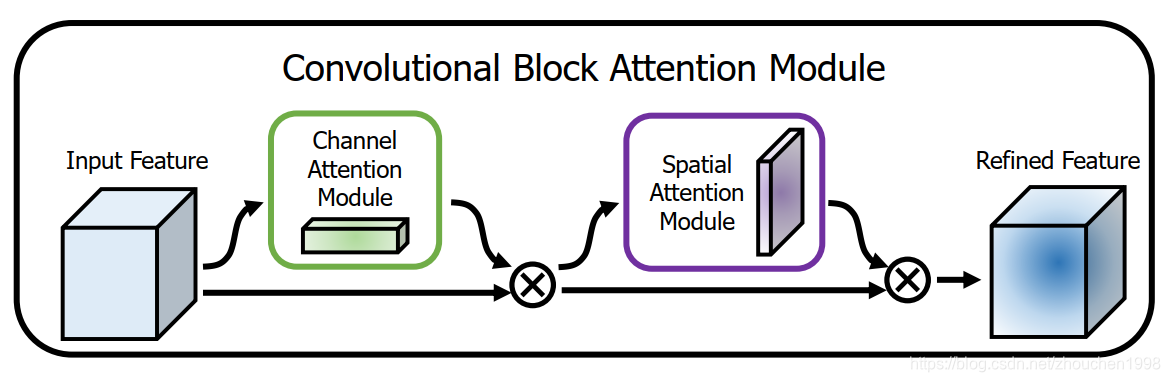
我们先从上图整体上看看CBAM怎么进行注意力的，首先，输入特征图F∈RC×H×W\mathbf{F} \in \mathbb{R}^{C \times H \times W}F∈RC×H×W和通道注意力图Mc∈RC×1×1\mathbf{M}_{\mathbf{c}} \in \mathbb{R}^{C \times 1 \times 1}Mc​∈RC×1×1逐通道相乘得到F′\mathbf{F'}F′，接着，F′\mathbf{F'}F′会和空间注意力图Ms∈R1×H×W\mathbf{M}_{\mathbf{s}} \in \mathbb{R}^{1 \times H \times W}Ms​∈R1×H×W逐位置相乘得到F′′\mathbf{F''}F′′，这就是CBAM的输出，它依然是$C\times H\times W$维度的。

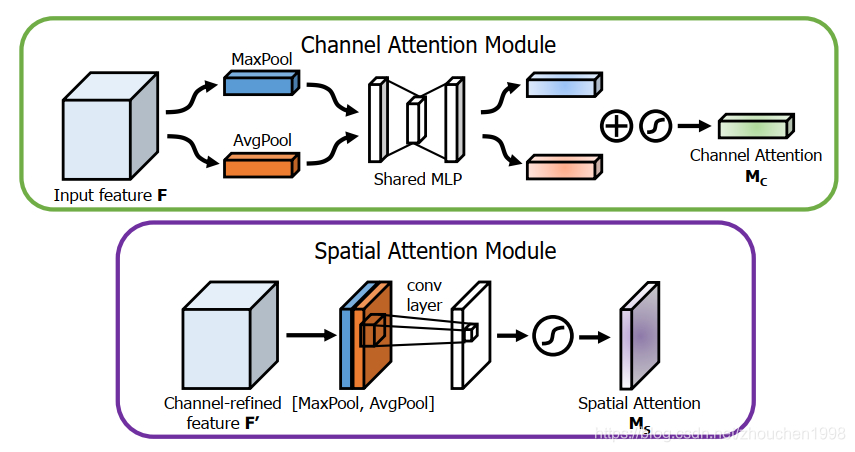
上图就是两个注意力模块的具体实现，我们先看通道注意力，它很类似于SENet，先是利用全局池化获得每个通道的位置全局信息，不过这里采用全局平均池化和全局最大池化分别得到Favgc\mathbf{F}_{\mathrm{avg}}^{\mathrm{c}}Favgc​和Fmaxc\mathbf{F}_{\mathrm{max}}^{\mathrm{c}}Fmaxc​，均得到一个$C\times 1\times 1$维的向量，经过共同的全连接层的降维再升维学习两个通道注意力（降维的维度用一个缩放比例控制），加到一起，获得的注意力图仍然是Mc(F)∈RC×1×1\mathbf{M}_{\mathbf{c}}(\mathbf{F}) \in \mathbb{R}^{C\times 1 \times 1}Mc​(F)∈RC×1×1。

再来看空间注意力，也是采用全局平均池化和全局最大池化，不过是沿着通道进行的，所以得到两个特征图Favg s∈R1×H×W\mathbf{F}_{\text {avg }}^{\mathbf{s}} \in \mathbb{R}^{1 \times H \times W}Favg s​∈R1×H×W 和 Fmax⁡s∈R1×H×W\mathbf{F}_{\max }^{\mathbf{s}} \in \mathbb{R}^{1 \times H \times W}Fmaxs​∈R1×H×W，然后将它们concat一起后使用一个7x7的卷积进行处理，得到Ms(F)∈1C×H×W\mathbf{M}_{\mathbf{s}}(\mathbf{F}) \in \mathbb{1}^{C\times H \times W}Ms​(F)∈1C×H×W。

将上述通道注意力图和空间注意力图按照下面的公式先后作用于输入特征图，就得到混合注意力的结果。至此，我们理解了CBAM模块的运行过程，其中的激活函数和BN等细节我没有提到，可以查看原论文，这里相比于BAM都采用了两个全局池化混合的方式，这在今天的网络中已经很常见了，属于捕获更加丰富信息的手段。

F′=Mc(F)⊗FF′′=Ms(F′)⊗F′\begin{aligned} \mathbf{F}^{\prime} &=\mathbf{M}_{\mathbf{c}}(\mathbf{F}) \otimes \mathbf{F} \\ \mathbf{F}^{\prime \prime} &=\mathbf{M}_{\mathbf{s}}\left(\mathbf{F}^{\prime}\right) \otimes \mathbf{F}^{\prime} \end{aligned} F′F′′​=Mc​(F)⊗F=Ms​(F′)⊗F′​

总结

本文简单介绍了计算机视觉中几种比较早期的采用注意力机制的卷积神经网络，它们的一些设计理念今天还被活跃用于各类任务中，是很值得了解的。后面的文章会介绍一些相对比较新的成果，欢迎关注。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！