3D数学基础:图形和游戏开发(第2版)第5章笔记
第5章 矩阵和线性变换
- 5.1 旋转(rotation)
- 5.2 缩放(scale)
- 5.3 正交投影(orthographic projectio)
- 5.4 反射(reflection)
- 5.5 错切(shearing)
- 5.6 组合变换
- 5.7 变换的分类
- 线性变换(Linear Transformations)
- 仿射变换( Affine Transformations
- 可逆变换( Invertible Transformations)
- 保持角度的变换(Angle-Preserving Transformations)
- 正交变换(Orthogonal Transformations)
- 刚体变换(Rigid Body Transformations)
- 转换类型总结
5.1 旋转(rotation)
在二维中,我们只能做一种旋转:绕一个点旋转(不包括平移)。
围绕原点的二维旋转只有一个参数,角θ,它定义了旋转的量。大多数数学书中的标准惯例是认为逆时针旋转为正,顺时针旋转为负。(然而,不同的约定适用于不同的情况。)
二维旋转矩阵
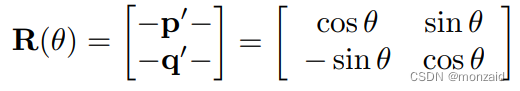
在三维中,旋转发生在轴上(不考虑平移),而不是点上,旋转轴不一定是x轴、y轴或z轴中的一个,旋转的方向遵循左手规则。
绕x轴旋转的三维矩阵
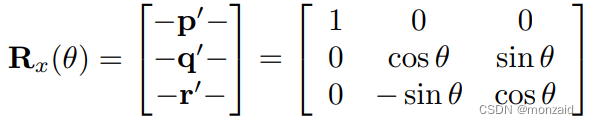
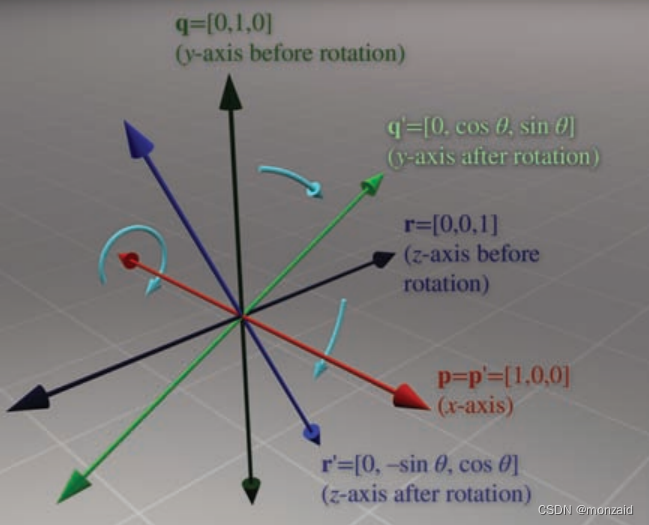
绕y轴旋转的三维矩阵
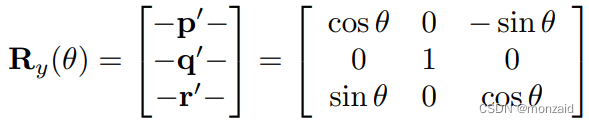
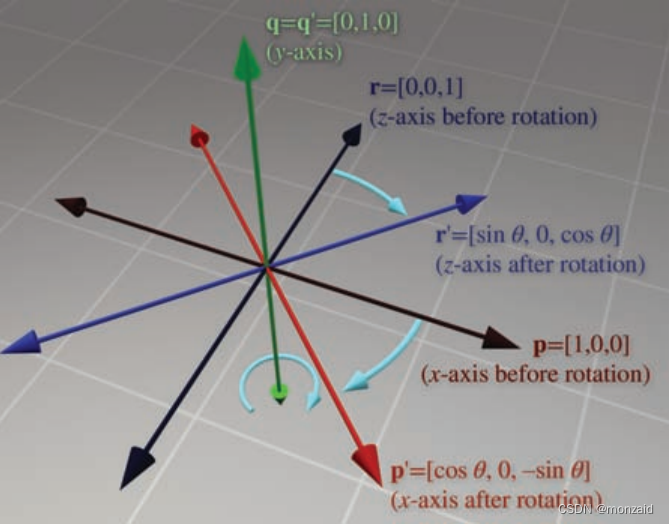
绕z轴旋转的三维矩阵

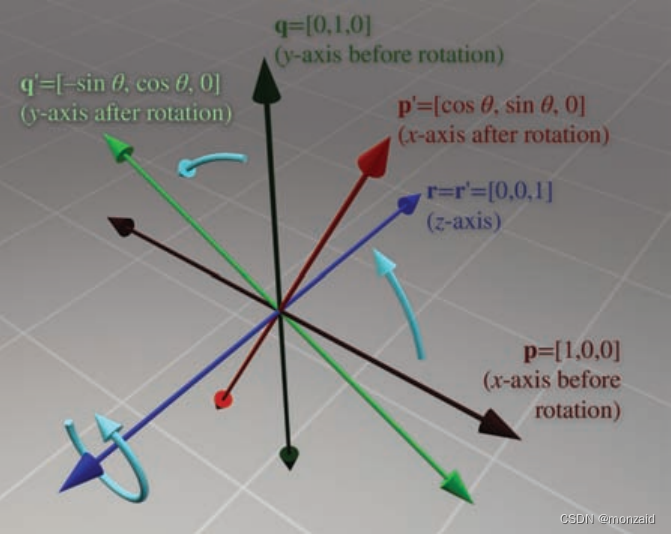
绕任意轴旋转的三维矩阵
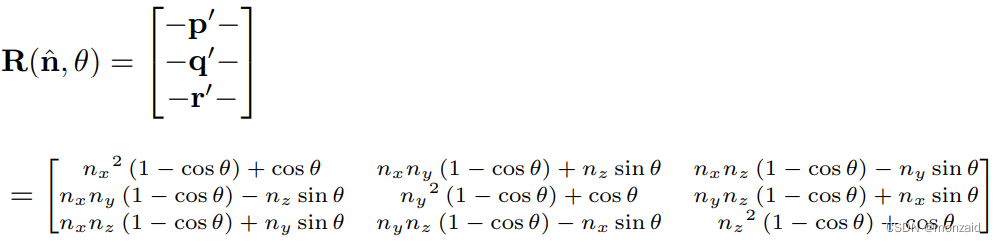
推导:
定义θ为绕轴旋转的量。轴将由单位矢量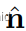 定义。
定义。
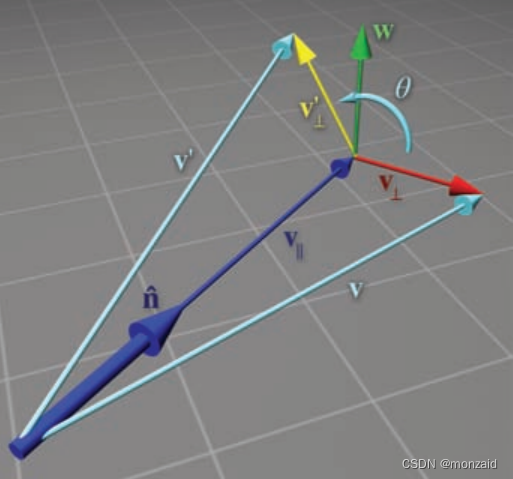
- 矢量w与
、
互相垂直,且与
长度相同。
绕
旋转90°即可构成。因此,w
=×
可以很容易地计算出它的值。
- 注意w和
组成了一个二维坐标空间,
是x轴,w是y轴。(注意,这两个向量不一定有单位长度)
是将
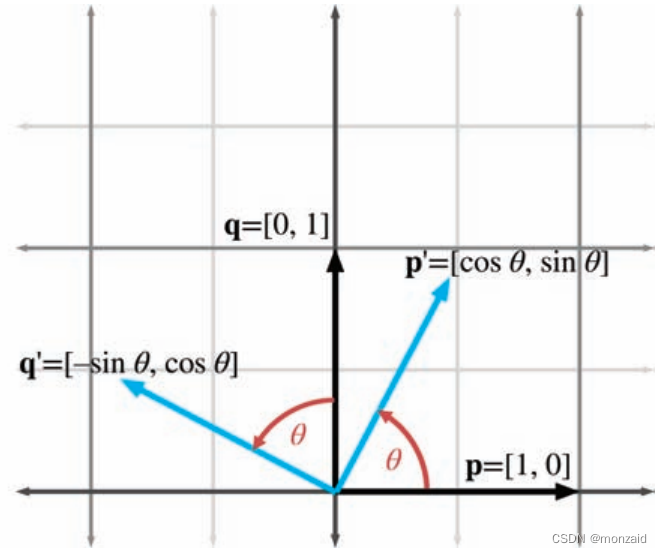
在这个平面内旋转θ角的结果。注意,这与将一个角度旋转到标准位置几乎相同。因此,
可以计算为:
计算过程:
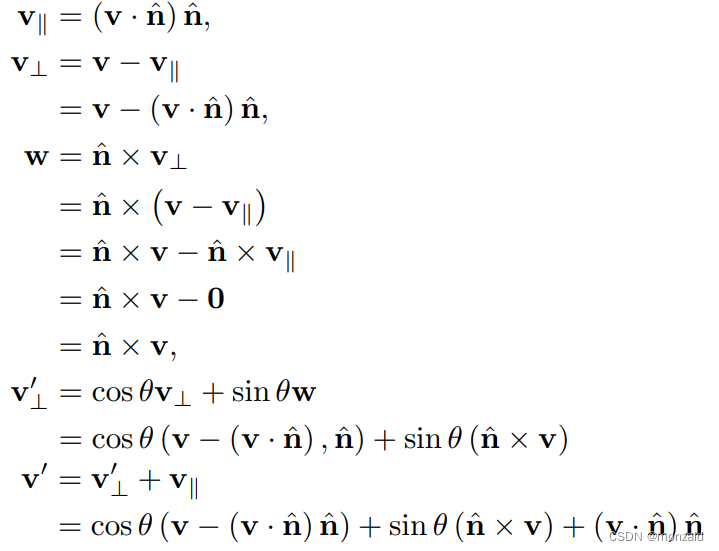
将矢量p,q,r分别带入v,得:
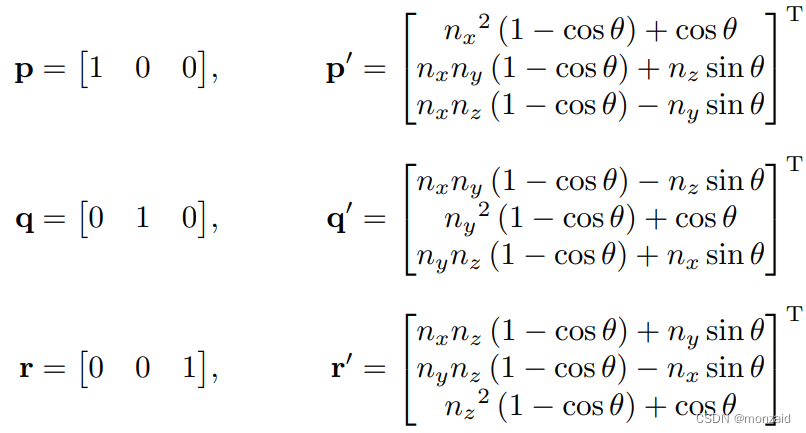
所以:
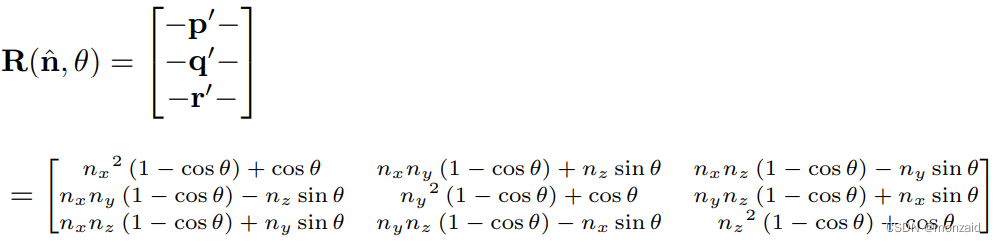
5.2 缩放(scale)
如果我们希望拉伸或挤压物体,我们可以在不同的方向上应用不同的比例因子,从而导致比例不均匀。非均匀尺度不能保持角度不变。长度、面积和体积是根据相对于尺度方向的方向变化的因素来调整的。
- 如果|k| < 1,那么物体在这个方向上变短。
- 如果|k| > 1,物体变长。
- 如果k = 0,那么我们获得一个正交投影,在第5.3节讨论。
- 如果k < 0,则我们获得一个反射,在第5.4节中介绍。
沿着主轴缩放

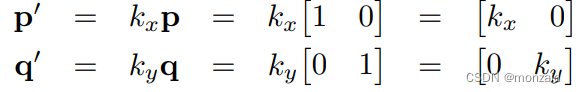


如果我们将任意向量乘以这个矩阵,那么,正如预期的那样,每个分量都被适当的比例因子缩放:
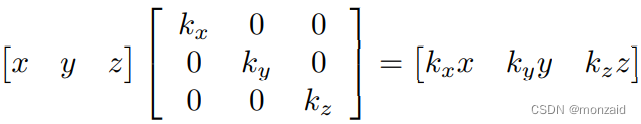
按任意方向缩放
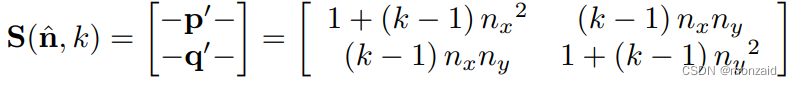
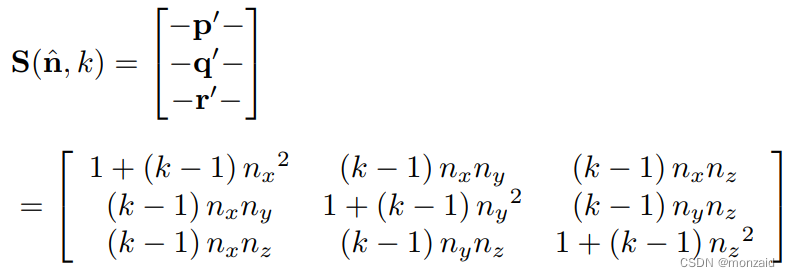
推导:
定义θ为绕轴旋转的量。轴将由单位矢量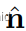 定义。
定义。
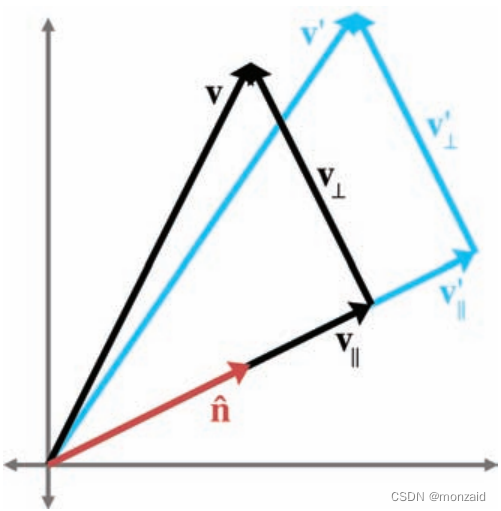
由于 垂直于
垂直于 ,不受缩放操作的影响。
,不受缩放操作的影响。
计算过程:
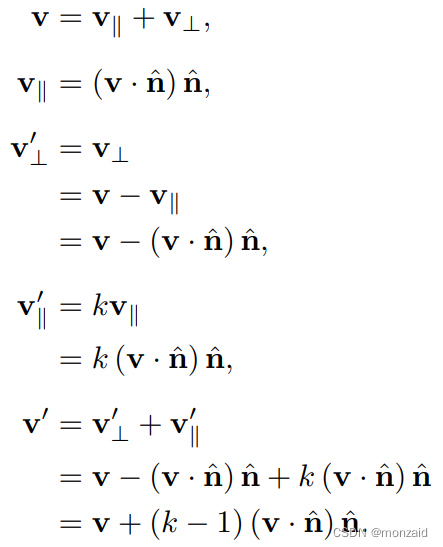
将矢量p,q分别带入v,得:

所以二维缩放矩阵:
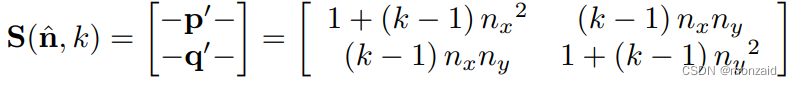
将矢量p,q,r分别带入v,得:
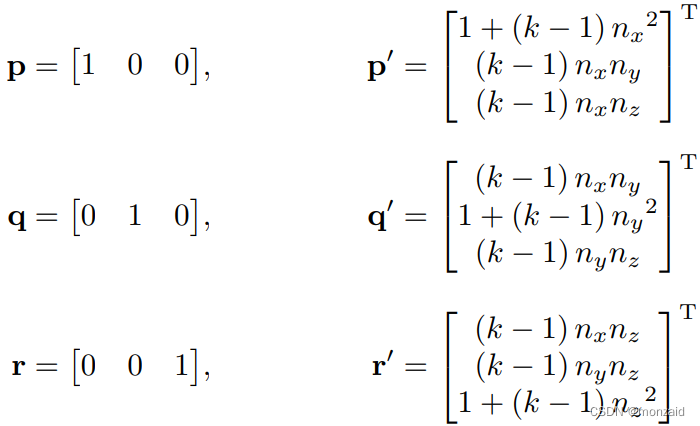
所以三维缩放矩阵:
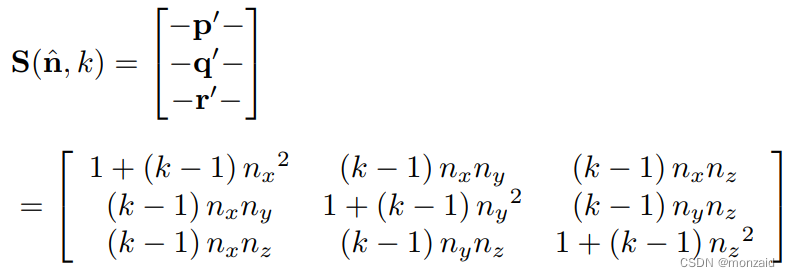
5.3 正交投影(orthographic projectio)
一般来说,投影一词指的是任何降维操作。
我们实现正交投影的一种方法是在一个方向上使用0的比例因子。在这种情况下,所有的点都被平放在垂直轴(在二维中1)或平面(在三维中)上。这种类型的投影是正交投影(orthographic projection),也被称为平行投影(parallel projection),因为从原始点到它们的投影对应点的线是平行的。

投影到主轴上(二维)
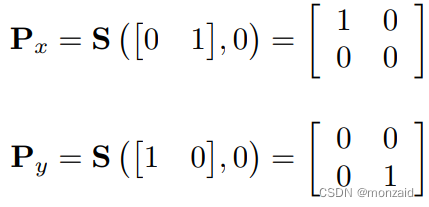
投影到主平面上(三维)
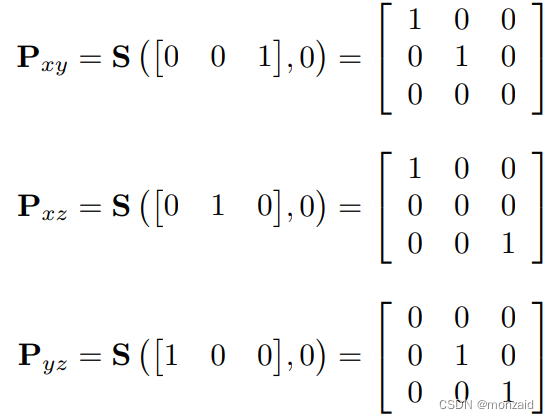
投影到任意直线上的二维矩阵,直线要穿过原点
将k = 0代入二维S(nˆ, k)缩放公式
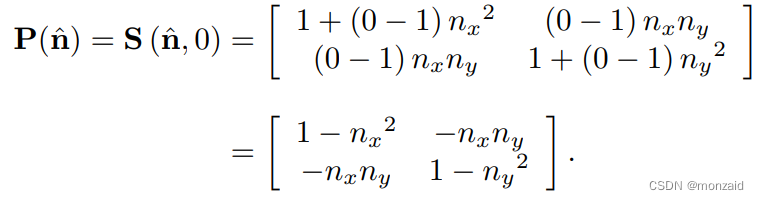
投影到任意平面上的三维矩阵,平面必须包含原点
将k = 0代入三维S(nˆ, k)缩放公式
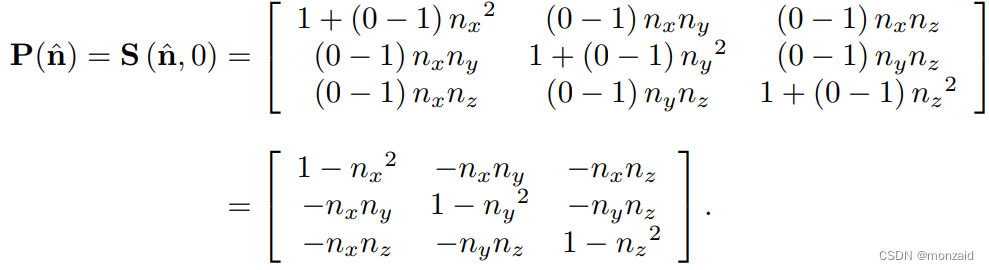
5.4 反射(reflection)
在二维中轴反射对象
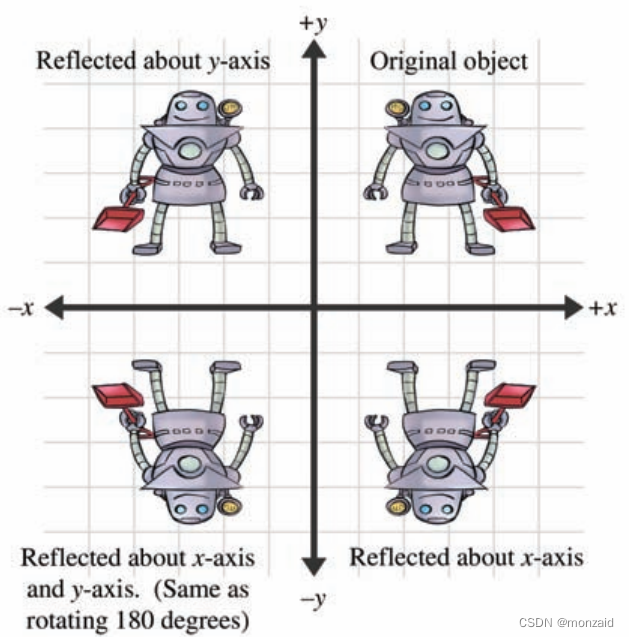
反射可以通过应用−1的比例因子来完成。设nˆ是二维单位向量。然后,由下式给出围绕穿过原点并垂直nˆ的反射轴来执行反射的矩阵(将k = -1代入二维S(nˆ, k)缩放公式):
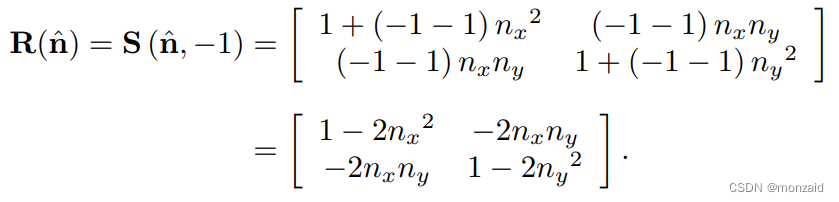
在三维中,我们有一个反射平面而不是轴。为了使变换是线性的,平面必须包含原点(将k = -1代入三维S(nˆ, k)缩放公式):
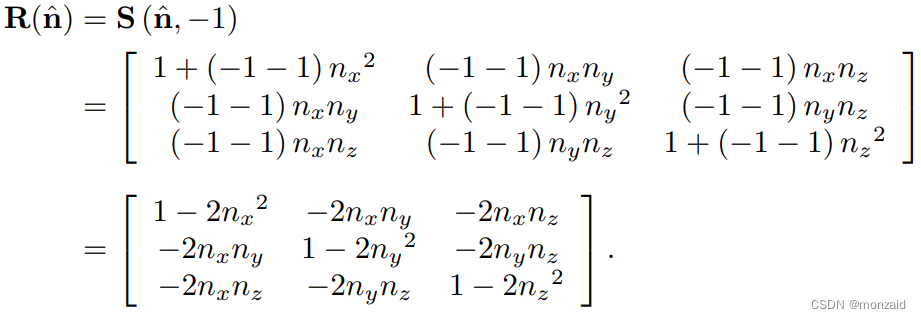
5.5 错切(shearing)
错切是一种使坐标空间“倾斜”的变换,它将不均匀地拉伸,角度没有保留;然而,面积和体积在错切后相等。
基本思想是将一个坐标的倍数加到另一个坐标上。

二维沿轴错切
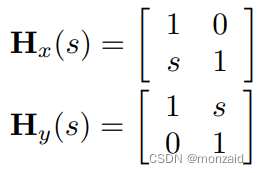
三维沿平面错切
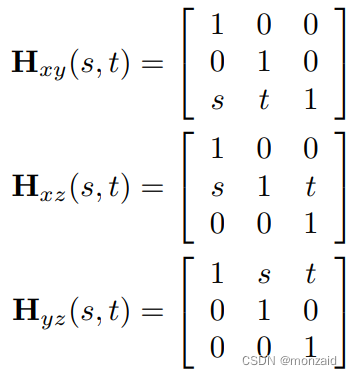
5.6 组合变换
例子:从对象空间转换到相机空间

5.7 变换的分类
线性变换(Linear Transformations)
包括旋转(rotation)、比例缩放(scale)、正交投影(orthographic projectio)、反射(reflection)、错切(shearing),不包括平移(translation)
形如v’ = vM
仿射变换( Affine Transformations
)
线性变换(Linear Transformations) + 平移(translation)
形如v’ = vM + b
可逆变换( Invertible Transformations)
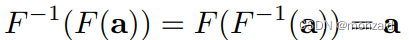
一个变换是可逆的:如果存在一个相反的变换,称为F的逆变换,它“撤销”了原始的变换。
除了投影,所有的原始变换都是可逆的。
保持角度的变换(Angle-Preserving Transformations)
如果两个向量之间的夹角在变换后在大小或方向上都没有改变,那么这个变换就是保持角度的。
正交变换(Orthogonal Transformations)
平移、旋转和反射是唯一的正交变换。所有正交变换都是仿射的并且可逆的。长度、角度、面积和体积都被保留。
正交矩阵保留角度、面积和体积的大小,但可能不保留符号。
正交矩阵的行列式是±1。
刚体变换(Rigid Body Transformations)
指改变物体的位置和方向,但不改变其形状。所有的角度、长度、面积和体积都保留了下来。
平移和旋转是唯一的刚体变换。反射不被认为是刚体变换。
刚体变换也称为合适变换(proper transformations)。
所有刚体变换都是正交的、保持角度的、可逆的、仿射的。
刚体变换是最严格的一类变换。
任意刚体变换矩阵的行列式都是1。
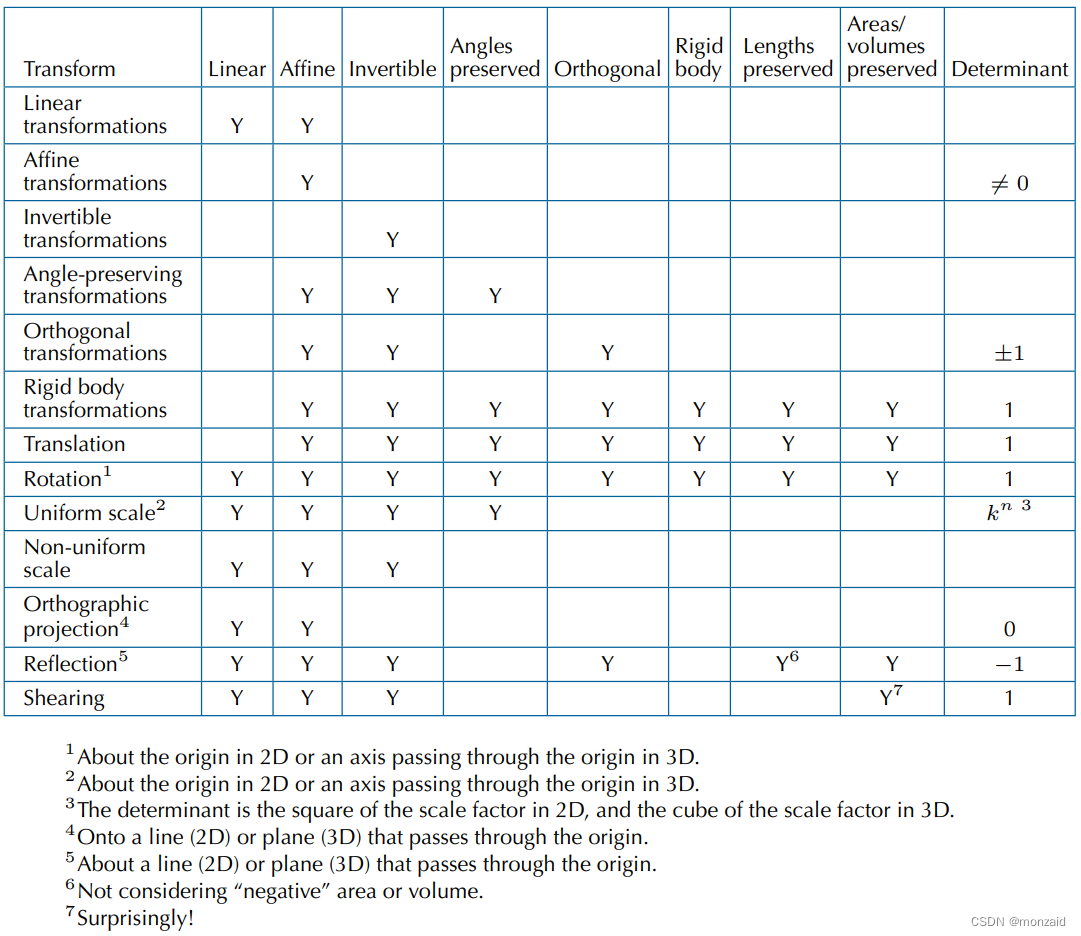
转换类型总结
在这个表中,Y表示该行中的转换总是具有与该列相关联的属性。没有Y并不意味着“从不”;相反,它的意思是“不总是”。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!