时序图神经网络（3）

2019

• 论文6 DyREP: Learning Representation over Dynamic Graphs
• • Motivation
  • Model
  • • 时间点过程
    • 嵌入表示学习
• 论文7 Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting
• • Motivation
  • Model
  • • Spatial Attention
    • Temporal Attention
    • Spatial-Temporal Convolution
• 论文8 Variational Graph Recurrent Neural Networks
• • Motivation
  • Model
  • • VGRNN
    • Semi-implicit VGRNN(SI-VGRNN)
• 论文9 Dynamic Graph Representation Learning via Self-attention Networks
• • Motivation
  • Model
  • • Structual Self-Attention
    • Temporal Self-Attention
• 论文10 Graph WaveNet for Deep Spatial-Temporal Graph Modeling
• • Motivation
  • Model
  • • 图卷积层
    • 时间卷积层
• 论文11 STG2Seq: Spatial-Temporal Graph to Sequence Model for Multi-step Passenger Demand Forecasting
• • Motivation
  • Model
  • • STG2Seq
    • Gated Graph Convolutional Module
    • Attention-based Output Module
• 论文12 Variational graph Auto-Encoders
• • 编码（学习均值和方差）
  • Inference Model（从分布中取Z）
  • Generative Model（从中间变量Z重新得到样本，解码）
• 损失函数

论文6 DyREP: Learning Representation over Dynamic Graphs

这篇文章发表于ICLR 2019，提出了模型DyREP。基于点过程建模图的动态变化，结合GAT（空域卷积）来捕捉空间特性。

Motivation

• 现在很多动态图建模方法都认为图的动态过程包括一种时间规模，但作者认为不是这样，现实世界中的图至少有两种时间规模的动态——Topological Evolution和Node Interaction，前者是指图的拓扑结构发生变化，后者是指节点属性值变化，并且作者在文中将这两种动态又命名为两种过程——association process和communication process。
• 现存的很多动态图嵌入学习的方法都没有以更细的时间粒度来捕捉特征。

Model

时间点过程

其在2017年也发表了一篇论文，其中有讲到时间点过程，作者认为时间点过程是一个随机过程，可以用密度函数来进行建模。
G t = ( V t , E t ) \mathcal{G}_t=(V_t,\mathcal{E}_t) Gt​=(Vt​,Et​)表示$t$时刻的图，可以看出此模型是针对图结构发生变化的无向同构图，在本论文中，作者只考虑了网络的增长，也就是边或者节点的增加。
当事件$p=(u,v,t,k)$发生时，先计算条件密度函数 λ k u , v = f k ( g k u , v ( t ‾ ) ) \lambda^{u,v}_k=f_k(g_k^{u,v}(\overline t)) λku,v​=fk​(gku,v​(t))，内部函数$g$计算节点$u,v$最新的兼容性： g k u , v ( t ‾ ) = w k T ⋅ [ z u ( t ‾ ) ; z v ( t ‾ ) ] g_k^{u,v}(\overline t)=w^T_k·[z^u(\overline t);z^v(\overline t)] gku,v​(t)=wkT​⋅[zu(t);zv(t)]。
计算得到的密度函数用于实时更新密度矩阵$S$和邻接矩阵$A$

嵌入表示学习

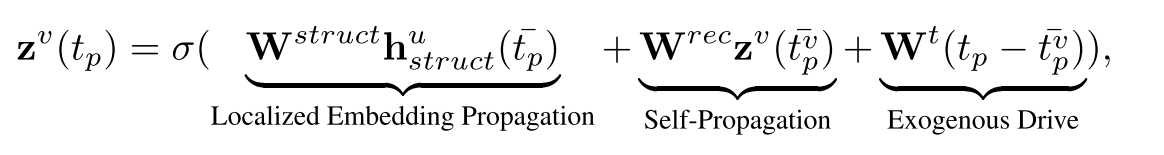
z v ( t p ) z^v(t_p) zv(tp​)表示 t p t_p tp​时刻节点$v$的嵌入表示，其由三个部分学习得到：

• 局部嵌入传播，也就是对邻域节点信息进行聚合，聚合采用的是注意力机制（有点类似GAT，也就这点和图卷积扯上了关系）：
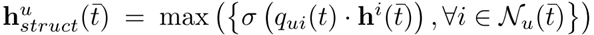
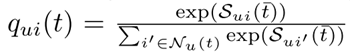
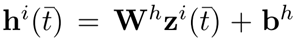
• 自传播：作者认为可能自身节点嵌入有相对于先前位置的转变，而不是随机变化；
• 某个外力驱动：作者认为可能有某种外力会随着时间对节点嵌入造成影响。

论文7 Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting

这篇文章发表于AAAI 2019。

Motivation

个人认为这篇论文的introduction和related work部分没有提到太有用的信息，ST-GCN没有考虑到交通数据的动态时空关联，这句话好抽象……大概的意思可能是：对于目标节点，其邻域的节点对其影响不同，且该影响程度会随着时间而发生变化，另外不同节点的历史序列对其的影响也不同。

Model

该模型针对的数据是图结构不发生改变的无向图。（处理的实际数据应该是不带权的，但不一定不能用于带权数据）
$$G=(V,E,A)$$

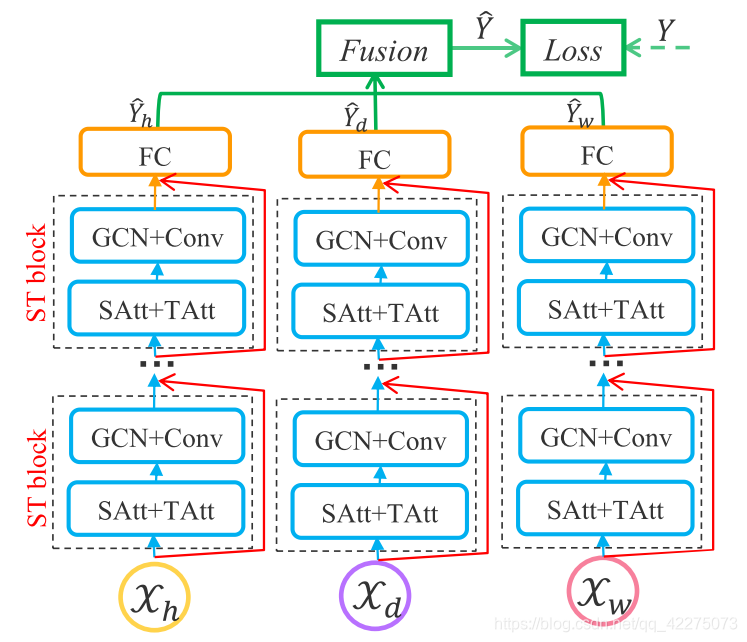
模型也非常简单，分成了三个独立的部分，分别建模最近时刻、天、周为周期的时间依赖。也就是将数据进行划分，得到不同周期的输入时间序列。SAtt和TAtt分别表示空间注意力和时间注意力。

Spatial Attention

第$r$层的空间注意力如下图：

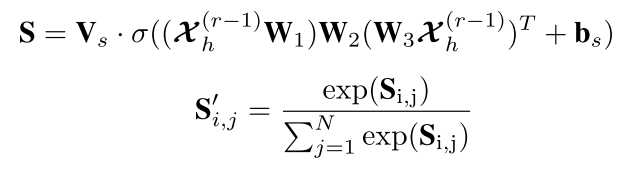
其中输入 X h ( r − 1 ) ∈ R N × C r − 1 × T r − 1 \mathcal{X}_h^{(r-1)}∈R^{N×C_{r-1}×T_{r-1}} Xh(r−1)​∈RN×Cr−1​×Tr−1​， T r − 1 T_{r-1} Tr−1​表示时间维度上的长度， C r − 1 C_{r-1} Cr−1​表示数据的channel数量， S i , j ′ S'_{i,j} Si,j′​表示节点$i$和$j$之间的关联强度，矩阵 S ′ S' S′将会乘上邻接矩阵$A$，来动态调整节点之间的影响。

Temporal Attention

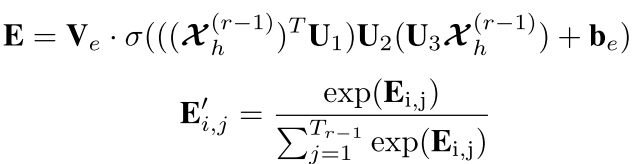
E i , j ′ E'_{i,j} Ei,j′​表示时间点$i$和$j$之间的关联强度，直接将时间注意力用于输入数据。

Spatial-Temporal Convolution

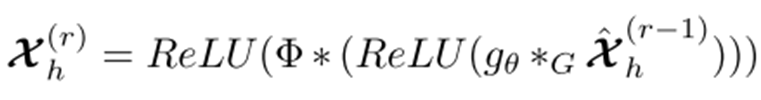
首先，对于输入数据进行时间维度的注意力处理，然后将该数据作为输入送入GCN进行卷积， g θ ∗ G g_\theta*G gθ​∗G表示包含空间注意力的GCN，GCN的结果送入时间卷积。

最后三个部分的输入连接，得到最终输出：

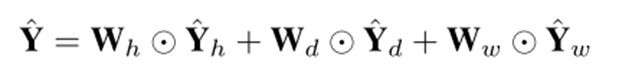
论文8 Variational Graph Recurrent Neural Networks

这篇文章发表于NIPS 2019。

Motivation

现存的方法都是用低维空间中一个确定性的向量来表示节点，这种确定性的表示缺少对节点嵌入的不确定性建模的能力（比如论文5的DyREP），这是当具有多个信息源（如节点属性和图结构）时必须考虑的因素。
GCRN的问题：每一个时间步的计算可以表示为 h t = f ( A , X ( t ) , h t − 1 ) h_t=f(A,X^{(t)},h_{t-1}) ht​=f(A,X(t),ht−1​)，当输入节点特征向量$X$的可变性很高时，GCRN仍企图将该可变性映射到隐藏状态$h$，也就导致了$h$的高可变性，最终导致模型过拟合。

Model

总体的看，作者首先基于GCRN（论文1）做出了改进，提出GRNN用于动态图，作者认为GRNN缺乏充分捕捉拓扑演化和时变节点属性之间复杂依赖关系的表达能力，又提出了VGRNN，最后为了进一步提高表达能力和可解释性，作者引入semi-implicit variational inference结合VGRNN，提出了SI-VGRNN。
如果不了解VGAE可以先看本文的最后一篇论文介绍。

VGRNN

在VGAE中，损失函数中有一个标准正态分布$p(\cdot )$，而这里的$p(\cdot )$不再是标准正态分布，而是基于hidden_state学习到的一个先验分布，作者认为这样做可以捕捉到图变化过程，从而学习到更灵活的潜在表示，其他的都和VGAE类似。

• 计算先验（只是用于损失函数的计算）
  
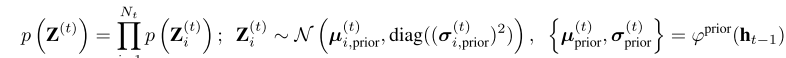
• 编码（Inference）
  
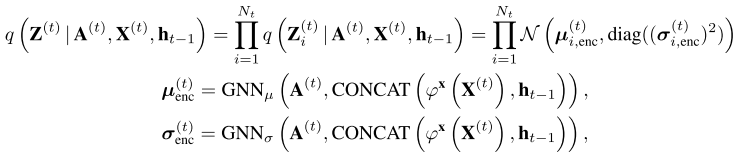
• 解码（Generation）
  
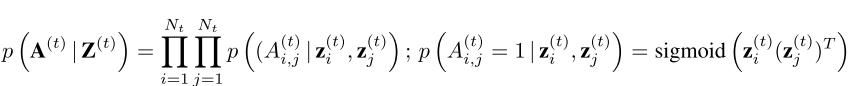
• 循环计算hidden state（Recurrence）
  
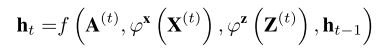
  注意上述式子的各种$\phi$可以是任何神经网络。

Semi-implicit VGRNN(SI-VGRNN)

VGRNN编码的过程是：针对$t$时刻的图，用图神经网络学习得到$\mu$和$\sigma$（均值和方差），然后在以$\mu$和$\sigma$为均值和方差的正态分布中选取$Z$；

SI-VGRNN编码的过程是：针对$t$时刻的图，用$L$层的stochastic layers学习得到 l j ( t ) l_j^{(t)} lj(t)​（对于第$j$层，随机噪声 ϵ j ( t ) ∼ q j ( ϵ ) \epsilon_j^{(t)}\sim q_j(\epsilon) ϵj(t)​∼qj​(ϵ)， l j ( t ) l_j^{(t)} lj(t)​结合 l j − 1 ( t ) l_{j-1}^{(t)} lj−1(t)​和 ϵ j ( t ) \epsilon_j^{(t)} ϵj(t)​以及时刻$t$的隐藏层状态 h t − 1 h_{t-1} ht−1​，学习到 l j ( t ) l_j^{(t)} lj(t)​），然后用 l j ( t ) l_j^{(t)} lj(t)​用图神经网络学习得到$\mu$和$\Sigma$（均值和方差），然后在以$\mu$和$\Sigma$为均值和方差的正态分布中选取$Z$；

具体的理论解释我确实没看懂……待更

论文9 Dynamic Graph Representation Learning via Self-attention Networks

这篇文章发表于ICLR 2019，提出了模型DySAT。

Motivation

现在的方法有的在节点表现出特别的演变行为时会效果不好，以及有的方法只对一阶邻域进行建模，忽略了高阶邻域的结构。（作者列举的这些前人方法好像都没有使用图卷积来做的）

Model

G = { G 1 , … , G T } G t = ( V , E t ) G=\{\mathcal{G}^1,\ldots,\mathcal{G}^T\}\\ \mathcal{G}^t=(V,\mathcal{E}^t) G={G1,…,GT}Gt=(V,Et)这篇论文是适用于图结构发生改变的带权有向图的动态建模，但是论文中假定节点一直是共享的，也就是不出现节点增减的情况，只有边增减的情况。
DySAT总体结构如下：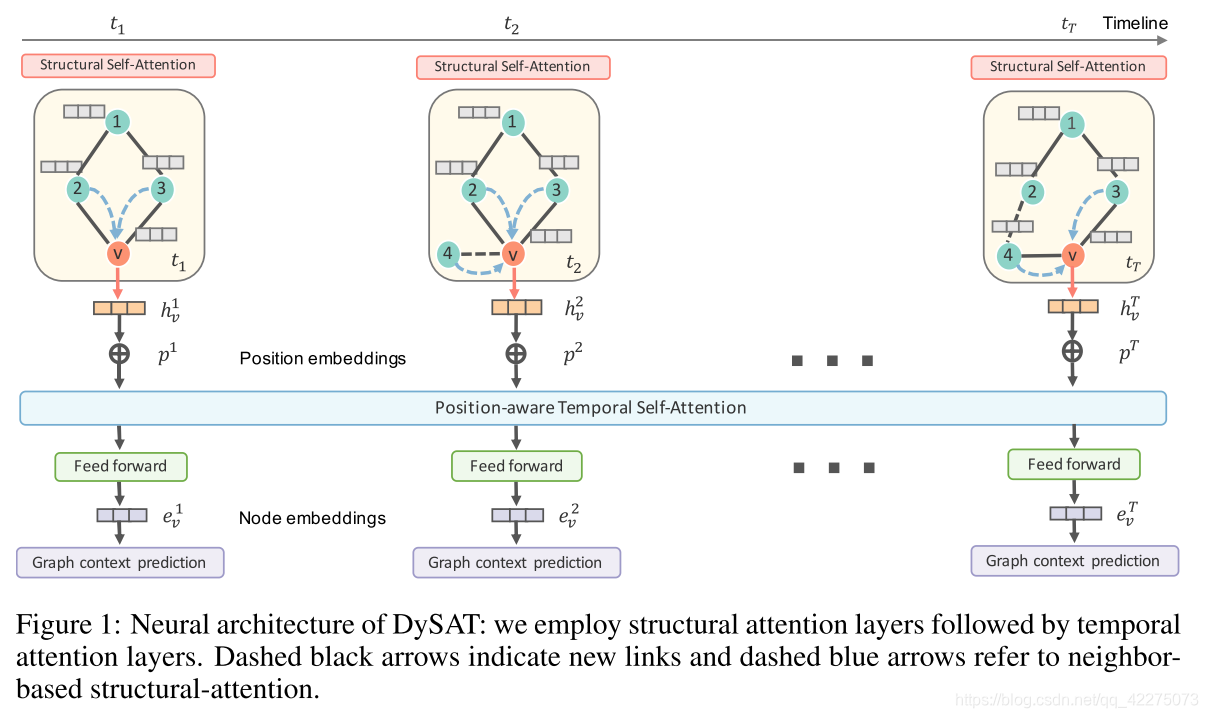
如图方法也很简单，首先对于每个时间帧，通过GAT对节点进行学习，得到的向量表示再作为temporal层的输入。

Structual Self-Attention

对于$t$时刻，Structual Self-Attention的输入是当前图结构$\mathcal{G}$和节点特征向量$X$，其中 x v ∈ R D x_v∈R^D xv​∈RD，输出是针对每个节点$v$， z v ∈ R F z_v∈R^F zv​∈RF。
Structual Self-Attention层只关注节点在当前时刻的邻域，注意力计算和GAT类似：

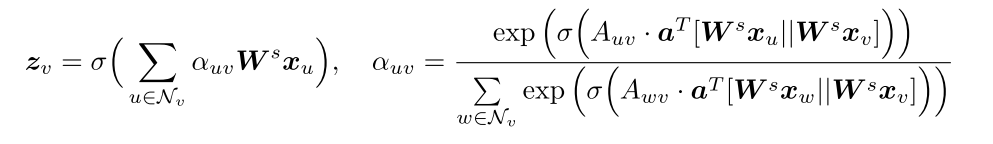
DySAT总体结构中用 h v h_v hv​表示本层的输出，也就是本层最终对于节点$v$，计算得到其在每个时刻聚合邻域后表示： { h v 1 , h v 2 , … , h v T } \{h_v^1,h_v^2,\ldots,h_v^T\} {hv1​,hv2​,…,hvT​}。

Temporal Self-Attention

这一层是对每个节点在时间维度上进行处理，对于节点$v$，在本层的输入为 x v 1 , x v 2 , … , x v T , x v t ∈ R D ′ {x_v^1,x_v^2,\ldots,x_v^T},x_v^t∈R^{D'} xv1​,xv2​,…,xvT​,xvt​∈RD′，本层的输出为 z v 1 , z v 2 , … , z v T , z v t ∈ R F ′ {z_v^1,z_v^2,\ldots,z_v^T},z_v^t∈R^{F'} zv1​,zv2​,…,zvT​,zvt​∈RF′。

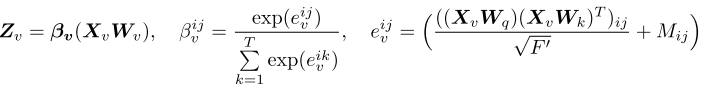
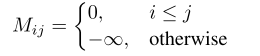
当$i>j$时， M i j = − ∞ M_{ij}=-\infty Mij​=−∞，得到的 β i j = 0 \beta^{ij}=0 βij=0，从而认为时刻$i$的节点$v$的表示对时刻$j$时的节点表示没有影响。从而避免靠后的时刻对靠前的时刻的节点编码造成影响。
DySAT总体结构中，本层的输入不仅仅是来自结构层的输出，还有对位置的编码， { p 1 , p 2 , … , p T } \{p^1,p^2,\ldots,p^T\} {p1,p2,…,pT}，表示每个图在时间维度上绝对位置。因而本层实际输入为 { h v 1 + p 1 , h v 2 + p 2 , … , h v T + p T } \{h_v^1+p^1,h_v^2+p^2,\ldots,h_v^T+p^T\} {hv1​+p1,hv2​+p2,…,hvT​+pT}，经过时间层的处理后，再紧跟一个前馈网络，最终得到节点在每个时间步的表示 { e v 1 , e v 2 , … , e v T } \{e_v^1,e_v^2,\ldots,e_v^T\} {ev1​,ev2​,…,evT​}。

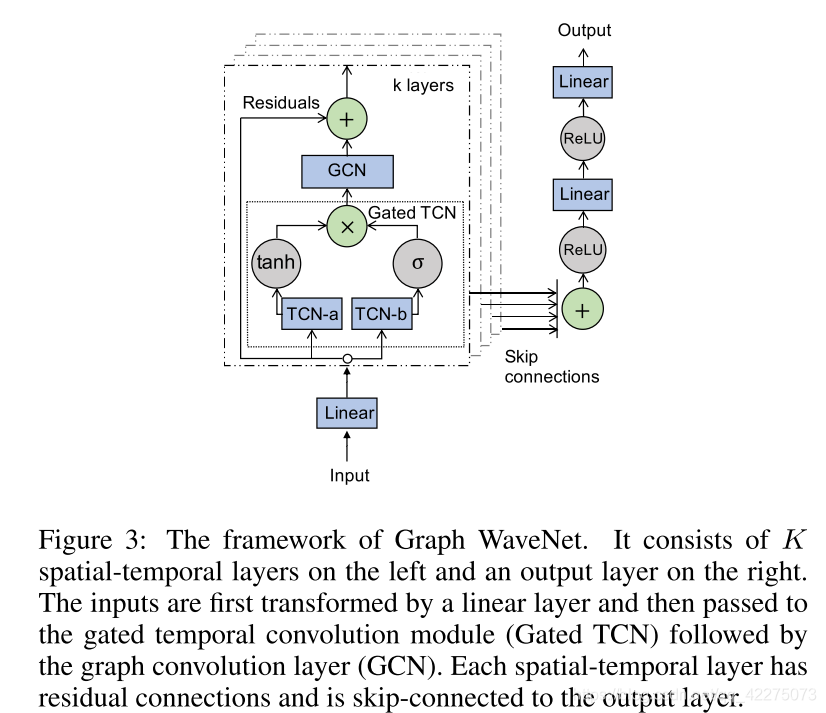
论文10 Graph WaveNet for Deep Spatial-Temporal Graph Modeling

这篇文章发表于IJCAI 2019。

Motivation

• 现有的研究都认为图结构反映了真实的节点之间的依赖关系，但作者认为不是这样的，比如在推荐系统中，两个用户之间相连，但他们也许有着完全不同的喜好，两个用户可能有相同的喜好，他们之间却并不一定连接；
• 目前的很多方法都使用RNN或者CNN来建模时序信息，而这些方法并不能用于long range的时序建模。比如GCRN、DCRNN、Structural-RNN、ST-GCN。

Model

G = ( V , E ) ; A i j = 1 o r 0 ; X ( t ) ∈ R N × D . G=(V,E);\\A_{ij}=1{\,}or {\,}0;\\X^{(t)}∈R^{N×D}. G=(V,E);Aij​=1or0;X(t)∈RN×D.这篇论文是针对图结构不发生变化的不带权有向图进行建模的。也就是对节点属性的动态变化进行建模。
[ X ( t − S ) : t , G ] → f X ( t + 1 ) : ( t + T ) [X^{(t-S):t},G]\stackrel{f}{\rightarrow} X^{(t+1):(t+T)} [X(t−S):t,G]→fX(t+1):(t+T)

图卷积层

这里作者借鉴了DCRNN中的扩散卷积，这样就用简单的GCN来建模有向图了：
Z = ∑ k = 0 K P f k X W k 1 + P b k X W k 2 P f = A / r o w s u m ( A ) P b = A T / r o w s u m ( A T ) Z=\sum_{k=0}^K P_f^kXW_{k1}+P_b^kXW_{k2}\\P_f=A/rowsum(A)\\P_b=A^T/rowsum(A^T) Z=k=0∑K​Pfk​XWk1​+Pbk​XWk2​Pf​=A/rowsum(A)Pb​=AT/rowsum(AT)
并且，作者提出了self-adaptive adjacency matrix的概念，从而发现节点之间隐藏的依赖关系：
A ~ a d p = S o f t M a x ( R e L U ( E 1 E 2 T ) ) \tilde{\mathbf{A}}_{adp}=SoftMax(ReLU(E_1E_2^T))\\ A~adp​=SoftMax(ReLU(E1​E2T​))其实就是学习两个向量 E 1 , E 2 E_1,E_2 E1​,E2​，表示节点嵌入词典，节点嵌入两两相乘就表示两点在空间上的依赖。
如果具备图的先验知识（也就是邻接矩阵），那么图卷积可以表示为：
Z = ∑ k = 0 K P f k X W k 1 + P b k X W k 2 + A ~ a d p X W k 3 Z=\sum_{k=0}^K P_f^kXW_{k1}+P_b^kXW_{k2}+\tilde{\mathbf{A}}_{adp}XW_{k3}\\ Z=k=0∑K​Pfk​XWk1​+Pbk​XWk2​+A~adp​XWk3​如果不具备图的先验知识，那就直接对自适应邻接矩阵进行卷积：
Z = ∑ k = 0 K A ~ a d p X W k 3 Z=\sum_{k=0}^K \tilde{\mathbf{A}}_{adp}XW_{k3}\\ Z=k=0∑K​A~adp​XWk3​

时间卷积层

作者使用dilated causal convolution作为时间卷积层，该方法相对于RNN的优点是以非递归的方式处理序列信息，可以并行计算并且避免梯度爆炸问题。
时间卷积层包含一个门结构和两个TCN
h = g ( Θ 1 ⋆ X + b ) ⊙ σ ( Θ 2 ⋆ X + b ) h=g(\Theta_1\star X + b)\odot\sigma(\Theta_2 \star X+b) h=g(Θ1​⋆X+b)⊙σ(Θ2​⋆X+b) Θ 1 \Theta_1 Θ1​和 Θ 2 \Theta_2 Θ2​表示两个dilated causal convolution。

论文11 STG2Seq: Spatial-Temporal Graph to Sequence Model for Multi-step Passenger Demand Forecasting

这篇文章发表于IJCAI 2019。这篇论文是为了解决一个实际问题：多个时间步的需求预测问题。

Motivation

基于RNN的预测模型由两个缺点：

• 在编码阶段，当$h$个历史序列输入时，就需要$h$个迭代的RNN单元来处理，因而待求的未来需求与历史的需求之间的计算距离太长，可能导致严重的信息遗忘；
• 在解码阶段，$T$时刻的预测需要隐藏层和$T-1$时刻的预测为输入，这样会导致前一个时刻的误差会影响本次预测，最终误差被逐步累积。

Model

该模型针对的数据是图结构不发生改变的带权无向图。（论文中没具体说数据，但其使用的是GCN，所以只能用于无向图，如果换成扩散卷积，可能有向图也可以）
这里的图结构是将城市分成N个小的网络区域，构成图$G$，邻接矩阵元素 A i j = 1 A_{ij}=1 Aij​=1时表示两个节点相似度超过某一阈值。
对于每个时间步，有两个输入特征向量： D t ∈ R N × d i n D_t∈R^{N×d_{in}} Dt​∈RN×din​表示N个区域的乘客需求， E t ∈ R d e E_t∈R^{d_e} Et​∈Rde​表示当前时刻的时间特征，比如当前是星期几，几点等信息。
目的就是预测未来的多个时间步乘客需求矩阵$D$：
( D t + 1 , D t + 2 , … , D T , … , D t + τ ) = Γ ( D t − h + 1 , D t − h + 2 , … , D t ; E 0 , E 1 , … , E t + τ ) (D_{t+1},D_{t+2},\ldots,D_T,\ldots,D_{t+\tau})=\Gamma(D_{t-h+1},D_{t-h+2},\ldots,D_t;E_0,E_1,\ldots,E_{t+\tau}) (Dt+1​,Dt+2​,…,DT​,…,Dt+τ​)=Γ(Dt−h+1​,Dt−h+2​,…,Dt​;E0​,E1​,…,Et+τ​)

STG2Seq

整体结构包括两条线路，长期编码和短期编码。

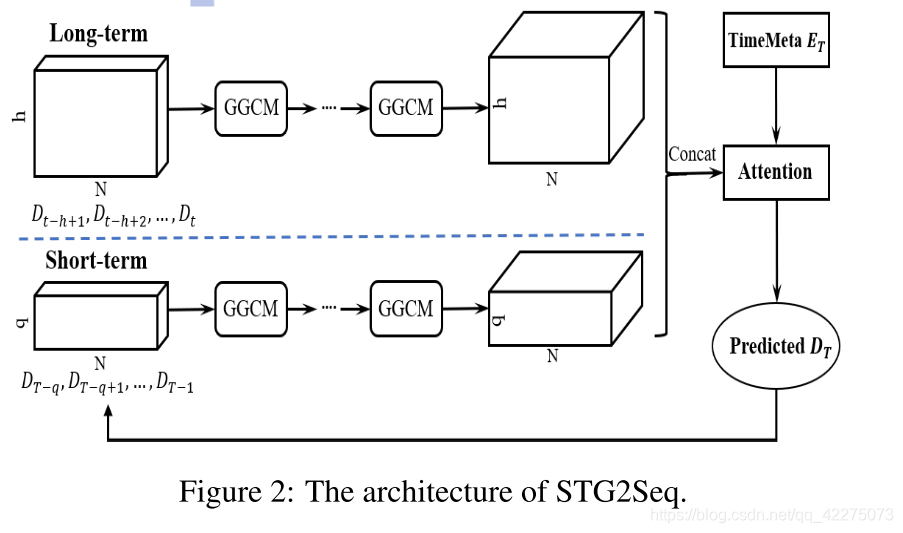
长期编码器以最近的$h$个时间步为输入，每个GGCM模块学习$k$个时间步的时间相关，那么只需要连续的 h − 1 k − 1 \frac {h-1} {k-1} k−1h−1​个GGCM，就可以捕捉到$h$个时间步的时间相关。最终得到输出为 Y h ∈ R h × N × d o u t Y_h∈R^{h×N×d_{out}} Yh​∈Rh×N×dout​。短期编码器也类似，不同的是$h$换成了$q$（更小的滑动窗口），输出为 Y q ∈ R q × N × d o u t Y_q∈R^{q×N×d_{out}} Yq​∈Rq×N×dout​。
注意：为了避免motivation的第二点，也就是长期预测的误差积累，虽然时间步$T$的预测被迭代地作为编码器的输入，但这里只用于短期编码器的输入，从而避免长期预测的不足。

Gated Graph Convolutional Module

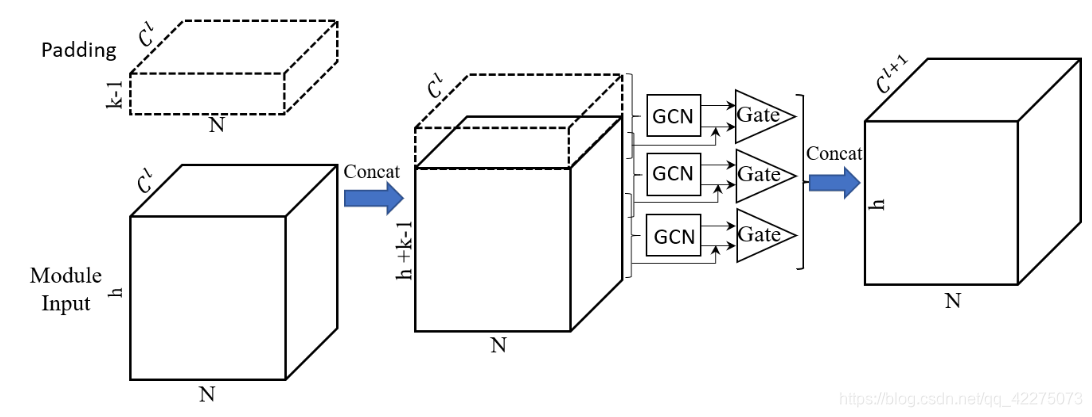
第 l t h l_{th} lth​层的输入尺寸为 h × N × C l h×N×C^l h×N×Cl，输出尺寸为 h × N × C l + 1 h×N×C^{l+1} h×N×Cl+1。

• 首先对输入加上一个 ( k − 1 ) × N × C l (k-1)×N×C^l (k−1)×N×Cl的零填充，这样的目的是避免经过处理后的序列长度减少。尺寸变为 ( h + k − 1 ) × N × C l (h+k-1)×N×C^l (h+k−1)×N×Cl；
• 每个GCN以$k$个时间步长的数据为输入 k × N × C l k×N×C^l k×N×Cl，对其进行reshape，得到 X ∈ N × ( k ⋅ C l ) X∈N×(k·C^l) X∈N×(k⋅Cl)，然后用门控GCN对其卷积处理： X l + 1 = ( ( P ~ − 1 2 A ~ P ~ − 1 2 ) X l W 1 + X l ) ⊗ σ ( ( P ~ − 1 2 A ~ P ~ − 1 2 ) X l W 2 ) X^{l+1}=((\tilde P^{-\frac 1 2}\tilde{A}\tilde{P}^{-\frac1 2})X^lW_1+X^l)\otimes\sigma((\tilde P^{-\frac 1 2}\tilde{A}\tilde{P}^{-\frac1 2})X^lW_2) Xl+1=((P~−21​A~P~−21​)XlW1​+Xl)⊗σ((P~−21​A~P~−21​)XlW2​)通过一个非线性的门来控制线性变换后的卷积结果作为输出。输出 X l + 1 ∈ R N × C l + 1 X^{l+1}∈R^{N×C^{l+1}} Xl+1∈RN×Cl+1；
• 将$h$个 X l + 1 ∈ R N × C l + 1 X^{l+1}∈R^{N×C^{l+1}} Xl+1∈RN×Cl+1结合，得到输出 h × N × C l + 1 h×N×C^{l+1} h×N×Cl+1。

下图是两个连续的GGCM提取时空信息的例子：

Attention-based Output Module

长期编码器和短期编码器的输出连接在一起得到 Y h + q ∈ R ( h + q ) × N × d o u t Y_{h+q}∈R^{(h+q)×N×d_{out}} Yh+q​∈R(h+q)×N×dout​， y i ∈ R N × d o u t y_i∈R^{N×d_{out}} yi​∈RN×dout​。

• temporal attention：由于不同的历史时刻对目标时刻的影响不同，且该影响随着时间而变化，所以在计算历史时刻的attention时，以编码后的联合表示和目标时刻的时间特征 E T E_T ET​为输入：
  
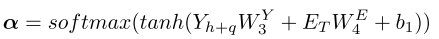
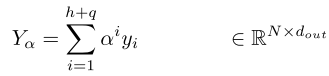
• channel attention：由于作者认为可能输出的不同channel对最终的结果也会有影响，作者在temporal attention后又增加了一个channel attention：
  

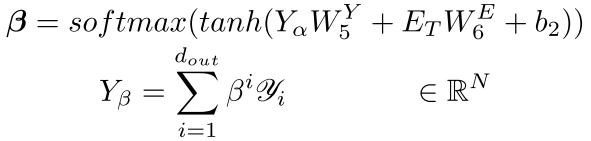
最终得到每个节点的需求预测。公式中得到的仅是一维的输出，作者提到可能需要多维的输出，那可以所求的多个维度都进行channel attention处理时，然后连接在一起即可。

论文12 Variational graph Auto-Encoders

这篇文章发表于NIPS 2016，由于论文7中用到了本论文中的想法，所以在此记录一下本篇论文的学习。（ps：https://zhuanlan.zhihu.com/p/78340397这篇讲的非常棒了）

给定一个不带权的无向图$G=(V,\mathcal{E})$，节点数为$N=|V|$，邻接矩阵为$A$（包含自连接），度矩阵$D$，节点特征矩阵 X ∈ R N × D X∈R^{N×D} X∈RN×D。

变分自编码器包括两个部分：编码器从学习样本中学到每个样本的低维向量表示分布（学习得到$\mu$和$\sigma$），并在该分布中采样出$Z$，解码器从$Z$中还原得到样本。

变分图自编码器也是差不多的结构。

编码（学习均值和方差）

σ = G C N σ ( X , A ) = A ~ R e L U ( A ~ X W 0 ) W σ μ = G C N μ ( X , A ) = A ~ R e L U ( A ~ X W 0 ) W μ \sigma=GCN_\sigma(X,A)=\tilde AReLU(\tilde AXW_0)W_\sigma\\ \mu=GCN_\mu(X,A)=\tilde AReLU(\tilde AXW_0)W_\mu σ=GCNσ​(X,A)=A~ReLU(A~XW0​)Wσ​μ=GCNμ​(X,A)=A~ReLU(A~XW0​)Wμ​

Inference Model（从分布中取Z）

q ( Z ∣ X , A ) = ∏ i = 1 N q ( z i ∣ X , A ) , q ( z i ∣ X , A ) = N ( z i , d i a g ( σ i 2 ) ) q(Z|X,A)=\prod_{i=1}^Nq(z_i|X,A),q(z_i|X,A)=N(z_i,diag(\sigma_i^2)) q(Z∣X,A)=i=1∏N​q(zi​∣X,A),q(zi​∣X,A)=N(zi​,diag(σi2​))

Generative Model（从中间变量Z重新得到样本，解码）

p ( A ∣ Z ) = ∏ i = 1 N ∏ i = 1 N p ( A i j ∣ z i , z j ) , p ( A i j = 1 ∣ z i , z j ) = σ ( z i T z j ) p(A|Z)=\prod_{i=1}^N\prod_{i=1}^Np(A_{ij}|z_i,z_j),p(A_{ij}=1|z_i,z_j)=\sigma(z_i^Tz_j) p(A∣Z)=i=1∏N​i=1∏N​p(Aij​∣zi​,zj​),p(Aij​=1∣zi​,zj​)=σ(ziT​zj​)注意区分上面几个式子中有两个$\sigma$，一个表示方差，一个表示激活函数。
两两计算节点之间存在边的可能性。

损失函数

学习的目标是为了学习得到能最好的表示样本的低维向量$Z$的分布，所以是优化权重矩阵W：
L = E q ( Z ∣ X , A ) [ l o g ( A ∣ Z ) ] − K L [ q ( Z ∣ X , A ) ∣ ∣ p ( Z ) ] L=E_{q(Z|X,A)}[log{\,}(A|Z)]-KL[q(Z|X,A)||p(Z)] L=Eq(Z∣X,A)​[log(A∣Z)]−KL[q(Z∣X,A)∣∣p(Z)]其中的$p(\cdot )$是作者采用的一个高斯先验核，就是一个标准正态分布 p ( Z ) = ∏ i p ( z i ) = ∏ i N ( z i ∣ 0 , I ) p(Z)=\prod_ip(z_i)=\prod_iN(z_i|0,I) p(Z)=∏i​p(zi​)=∏i​N(zi​∣0,I)，也就是说KL项计算的是各独立正态分布和标准正态分布之间的散度。
（损失函数我也不太理解，可以了解一下variational lower bound这个概念）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！