谈谈描述性分析思维
编辑导语:描述性分析思维的建立有助于帮助我们树立数据分析思维,具体而言,描述性分析思维有哪些思维维度和常见的数据指标?又该如何应用?本篇文章里,作者就描述性分析思维谈了谈他的见解和思路,不妨来看一下。
一、前言
之前梳理了“数据思维”概念、培养锻炼以及应用的一些相关的内容,现在我们将开始梳理一些做数据分析需要具备哪些常见的、实用的、具体的数据分析思维,如描述性分析思维、二八和帕累托思维、PEST分析思维、生命周期分析思维、竞品分析思维、结构化分析思维等。
本文将从数据分析入门级思维——描述性分析思维开始梳理,从而帮助大家树立数据分析思维的意识。
在做数据分析之前,我们首先要认识了解数据,将会收集一系列复杂的数据信息,对相关的数据进行统计整理。
在这种情况下,仅单靠让人“看”数据,会让人一脸茫然失措的。就像有些人不懂得如何更好地展示分析结果和数据来印证自己的分析,如一个人满腹经纶却不知该如何一展雄才。
想让人了解数据的大致情况、印证自己的分析时,利用描述性分析思维,就能让我们了解到数据信息的整体概况,还能让我们观察到数据的特征和异常问题等。
描述性分析思维,即对调查总体所有变量的有关数据做统计性描述,主要包括数据的频数分析、集中趋势分析、离散程度分析、分布和一些基本的可视化统计图形以及清晰的文字描述。
二、描述性分析思维有哪些指标?
所谓指标是帮助我们打开思路,通过多个指标对数据进行深度解读,不能仅仅靠着对数据的一种感觉和敏感来进行数据分析,这样的主观性太强。因此,我们来看一下描述性分析思维有哪些指标?

常用的描述性统计分析指标有:平均值、四分位数、方差、标准差、中位数、众数等。通过这些指标的计算和图形视觉化展示,让我们发现原来这些数据是这样的情况!
1. 平均值
平均值顾名思义就是计算数据的平均数是多少,可以让我们了解到数据的平均水平是多少。
公式:平均值μ=(数值X1+X2+X3……)/N(多少项,数值的数量)
优点:计算简单,可让人了解到平均水平如何。
缺点:当数据值差距很大的时候,呈现的平均水平结果就可能会出现不客观的现象,出现平均数陷阱,让人误解。例如,我们总觉得自己的收入水平拉低了城市人均工资的水平线。
2. 众数
众数(Mode):统计分布上具有明显集中趋势点的数值,代表数据的一般水平(众数可以不存在或多于一个)。
3. 中位数
中位数描述数据中心位置的数字特征。大体上比中位数大或小的数据个数为整个数据的一半。对于对称分布的数据,均值与中位数比较接近;对于偏态分布的数据,均值与中位数不同。中位数的又一显著特点是不受异常值得影响,具有稳健性,因此它是数据分析中相当重要的统计量。
4. 方差、标准差、标准分
方差:样本中各数据与样本平均数的差的平方和的平均数叫做样本方差;样本方差的算术平方根叫做样本标准差。样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。
标准分也叫z分数,是一种具有相等单位的量数。它是将原始分数与团体的平均数之差除以标准差所得的商数,是以标准差为单位度量原始分数离开其平均数的分数之上多少个标准差,或是在平均数之下多少个标准差。它是一个抽象值,不受原始测量单位的影响,并可接受进一步的统计处理。
用公式表示为:z=(x-μ)/σ;其中z为标准分数;x为某一具体分数,μ为平均数,σ为标准差。
标准分表示【某个数值】距离平均值多少个标准差。在质量管理中,我们常常听到6西格玛管理就是标准分的典型应用。这个标准差,通常用每百万次采样数的缺陷率来衡量。
1个标准差,就是每万件抽样中,有69万个不合格,相当于一本书每页有170个错别字。3个标准差就是每百万件抽样中,有6.7万个不合格,相当于一本书每页有1.5个错字。6个标准差就是每百万件抽样中,有3.4个不合格,相当于整个小型图书馆的所有藏书中,只有1个错别字。
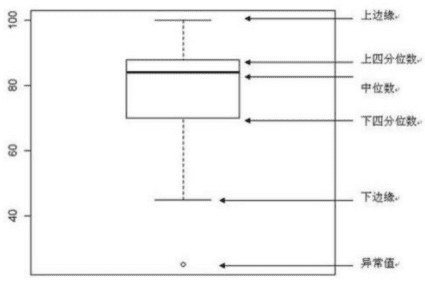
5. 四分位数
四分位数是指在把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值,分割后我们会通过5个数值来描述数据的整体分布情况。
下界:最小值,即第0%位置的数值;
下四分位数:Q1,即第25%位置的数值;
中位数:Q2,即第50%位置的数值;
上四分位数:Q3,即第75%位置的数值;
上界:最大值,即第100%位置的数值。
优点:可以用来对比不同类别数据的整体情况,还可以识别出可能的异常值。
缺点:无法反映数据的波动大小。
6. 极差
极差=最大值-最小值,是描述数据分散程度的量,极差描述了数据的范围,但无法描述其分布状态。且对异常值敏感,异常值的出现使得数据集的极差有很强的误导性。
7. 偏度
偏度用来评估一组数据的分布呈先的对称程度,即以正态分布为标准描述数据对称性的指标。
8. 峰度
峰度用来评估一组数据的分布形状的高低程度,即描述正态分布中曲线峰顶尖哨程度的指标。然而:
均值、中位数、众数体现了数据的集中趋势。
极差、方差、标准差体现了数据的离散程度。
偏度、峰度体现了数据的分布形状。
以上是常用的描述性分析的指标,还有一些其他的指标,如绝对数、相对数:倍数、成数、百分数等,这里就不一一介绍了。
三、描述性分析思维维度有哪些?
其实,在日常的数据分析中我们经常使用一些特征值,尤其是我们做周报或者月报的分析时,这些描述性的统计分析特征值对于我们有一定的帮助,描述性统计分析是进行正确的统计推断的先决条件。可通过数据的集中趋势、离散程度、分布类型和特点等维度进行初步分析。
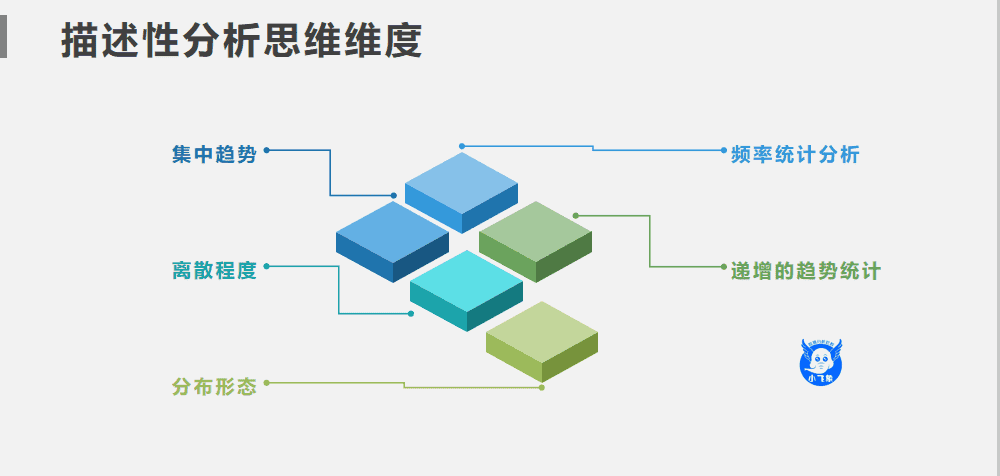
1. 集中趋势的描述性统计
均值:描述一组数据的平均水平,是集中趋势中波动最小、最可靠的指标,但是均值容易受到极端值(极小值或极大值)的影响。
中位数:最适合的表征集中趋势的指标。
众数:常用于描述定性数据的集中趋势,不受极端值的影响。
2. 离散程度的描述性统计
最大值和最小值:是一组数据中的最大观测值和最小观测值。
极差:一般情况下,极差越大,离散程度越大,其值容易受到极端值的影响。
方差和标准差:是描述一组数据离散程度的最常用、最适用的指标,值越大,表明数据的离散程度越大。
3. 分布形态的描述性统计
偏度:当偏度=0时,分布是对称的;当偏度>0时,分布呈正偏态;当偏度<0时,分布呈负偏态。
峰度:当峰度=0时,分布和正态分布基本一直;当峰度>0时,分布形态高狭;当峰度<0时,分布形态低阔。
4. 频率统计分析
频数分布分析(又称频率分析)主要通过频数分布表、条形图和直方图、百分位值等来描述数据的分布特征。
在做频数分布分析时,通常按照定性数据(即分类的类别),统计各个分类的频数,计算各个分类所占的百分比,进而得到频率分布表,最后根据频率分布表来绘制频率分布图。
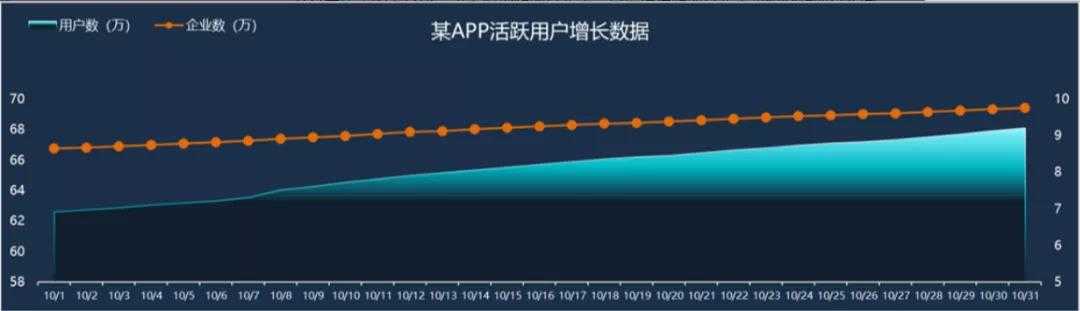
5. 按照时间递增的趋势统计
特殊情况下,当X轴是日期数据,Y轴是统计量(比如均值、总数量)时,可以绘制出统计量按照时间递增的趋势图,从图中可以看到统计量按照时间增加的趋势(无变化、递增或递减)和周期性。
例如,下图的X轴是日期,Y轴的统计量是总数量,两条折线分别是新增企业数和新增用户数据
四、描述性分析思维运用基本思路?
那么,接下来,我们来梳理一下描述性分析思维运用的基本思路?
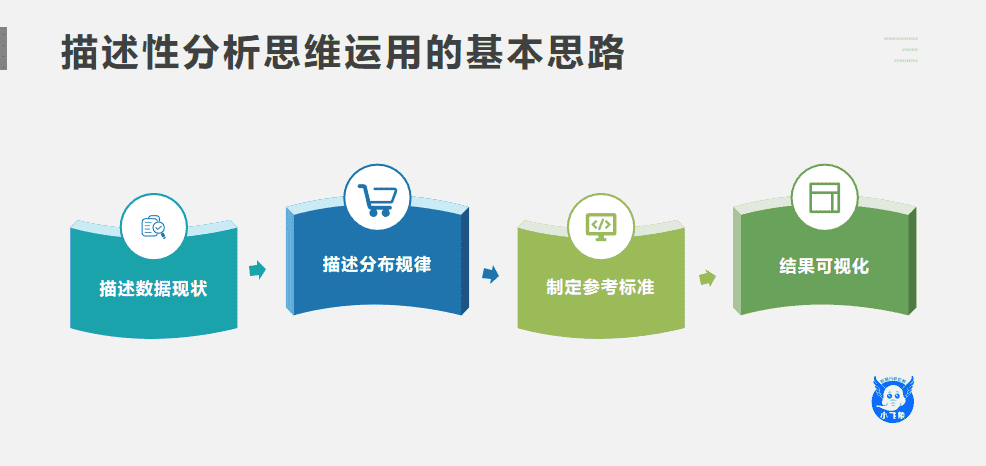
首先,要描述目前的数据表现的现状是什么,根据分析目的,提取指标数据的具体数值:如数量、平均数、极差、标准差、方差、极值。
其次,描述分布规律:如均匀分布、正态分布、集中趋势、长尾分布。
然后,根据以往的数据的或者是之前制定的标准,制定参考标准。
最后,综合现状和标准,输出有价值的结论,并进行可视化:如柱状图、条形图、散点图、饼状图。
只有业务概况+数据指标+标准(可视化)才能得出一个“是什么”的结论。
业务概况+数据指标+标准(可视化)=结论的分析流程,非常简单,不过标准如何去制定?那又是需要我们深思的问题了。
例如,一个门店购买商品的数量的平均值是多少?四分位数是多少?标准差是多少?标准分是多少?两个数据的变异系数是多少?
一个门店销量每日增长趋势怎么样?客单价的分布如何?成什么分布?门店总销量是多少?哪个商品卖得最好?细分的品类中卖的最好的是什么?
例如面包中,是有奶油面包的好,还是无脂面包=卖的好?什么时间用户购买最集中,一天中哪个时间段购买最集中,卖得最好?
五、总结
描述性分析思维,即解决业务现状“是什么”的问题,这是最基础的、最直观简洁的数据思维。但是由于简单,对多元变量的关系难以描述。现实生活中,自变量通常是多元的:决定体重不仅有身高,还有饮食习惯,肥胖基因等等因素。
但可以通过一些高级的数据处理手段,对多元变量进行处理,例如特征工程中,可以使用互信息方法来选择多个对因变量有较强相关性的自变量作为特征,还可以使用主成分分析法来消除一些冗余的自变量来降低运算复杂度。
在之后我们会提到拆解思维、对比思维等数据分析思维中都会涉及。总之,以后运用数据分析思维做得多了,做数据分析输出的成果就更严谨,有依据,有说服力,不在停留“取数”阶段了。
作者
木兮擎天@,微信公众号:木木自由,多年互联网数据运营经验,涉猎运营领域较广,关注于运营、数据分析的实战案例与经验以及方法论的总结,探索运营与数据的神奇奥秘!
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
