机器学习之决策树算法
一、什么叫决策树?
决策树(Decision Tree),又称判断树,它是一种以树形数据结构来展示决策规则和分类结果的模型,作为一种归纳学习算法,其重点是将看似无序、杂乱的已知实例,通过某种技术手段将它们转化成可以预测未知实例的树状模型,每一条从根结点(对最终分类结果贡献最大的属性)到叶子结点(最终分类结果)的路径都代表一条决策的规则。
二、决策树的原理是什么?
决策树(Decision Tree),是一种树状结构,上面的节点代表算法的某一特征,节点上可能存在很多的分支,每一个分支代表的是这个特征的不同种类(规则),最后叶子节点代表最终的决策结果。
决策树的构造只会影响到算法的复杂度和计算的时间,不会影响决策的结果。
为了更直观地理解决策树,我们现在来构建一个简单的邮件分类系统,如图:
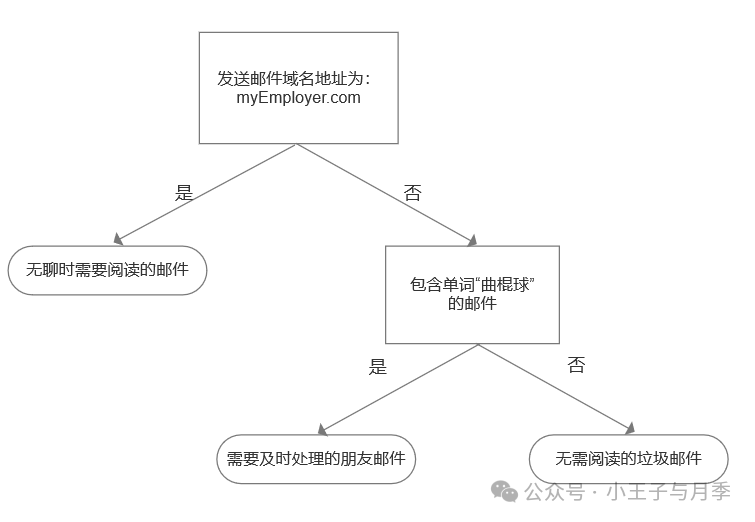
- 首先检测发送邮件域名地址;
- 如果地址为com,则放置于“无聊时需要阅读的邮件”分类;
- 如果不是这个地址,那么再次检测;
- 检查邮件是否有单词“曲棍球”;
- 包含单词“曲棍球”,则放置于“需要及时处理的朋友邮件”分类;
- 不包含单词“曲棍球”,则放置于“无需阅读的垃圾邮件”分类。
现在,我们来总结一下决策树的构成:
- 根节点。第一个需要判断的条件,往往也是最具有特征的那个条件,我们称为根节点。
- 中间节点。那个矩形总是要往下分,并不是最终的结果,它叫做中间节点(或内部节点)。
- 边。那些带有文字的线段(一般使用有箭头的有向线段),线的一端连的是中间节点、另一端连的是另一个中间节点或叶节点,然后线段上还有文字,它叫做边。
- 叶节点。那个圆角矩形,它就已经是最后的结果了,不再往下了,这一类东西呢,在决策树里叫做叶节点。
三、决策树的构造步骤
- 数据准备:首先对数据进行预处理,包括缺失值填充、异常值处理以及特征编码等操作。
- 特征选择:在每个内部节点上,计算所有特征的基尼不纯度(CART)或信息增益(ID3),选取具有最小不纯度/最大增益的特征作为划分标准。
- 生成分支:根据选定特征的最佳分割点,将数据集划分为子集,并为该节点创建分支。
- 递归生长:对每个子集重复上述过程,直至满足停止条件,如达到预设的最大深度、叶子节点包含样本数量少于阈值或者信息增益不再显著提高等。
- 剪枝优化:为了防止过拟合,可以通过后剪枝或预剪枝方法来简化决策树结构,提升模型泛化能力。
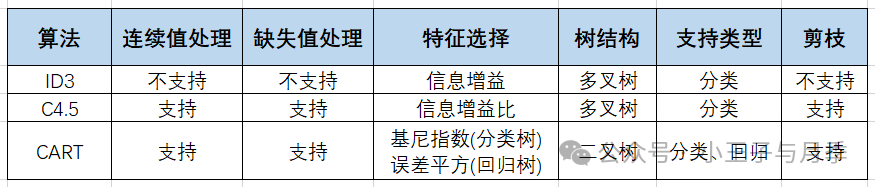
四、决策树的分类有哪些?
1. CART(Classification and Regression Tree)
Breiman.L.I等人在1984年提出了CART算法,即分类回归树算法。CART算法用基尼指数(Gini Index)代替了信息熵,用二叉树作为模型结构,所以不是直接通过属性值进行数据划分,该算法要在所有属性中找出最佳的二元划分。CART算法通过递归操作不断地对决策属性进行划分,同时利用验证数据对树模型进行优化。
处理问题类型:分类或回归
结构:二叉树结构
计算指标:分类问题是基尼系数,回归问题的指标是偏差
特点:可以处理缺失值,连续值,可以剪枝,避免过拟合。即可以处理分类问题,也可以处理回归问题。
CART中用于选择变量的不纯性度量是Gini指数,总体内包含的类别越杂乱,GINI指数就越大(跟熵的概念很相似)。
基尼系数公式如下:
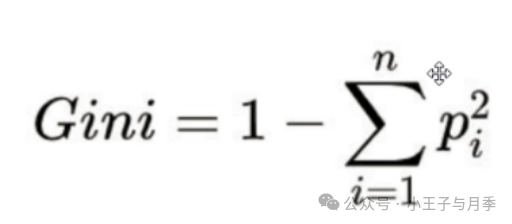
举例:
数据集D的纯度可用基尼值来度量:
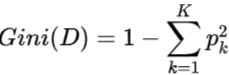
属性a的基尼指数定义为加权基尼指数:
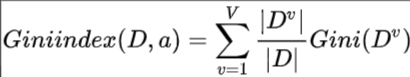
如何理解上面的公式呢?我们简单举个例子:
样例数据
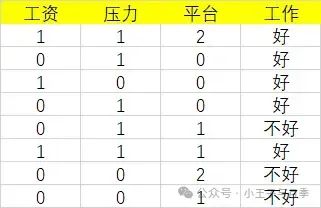
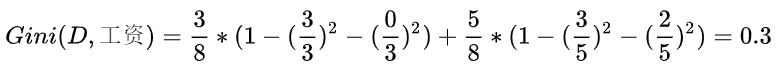
简单解释下为啥要这样算。
首先工资有两个取值,分别是0和1。当工资=1时,有3个样本。
所以: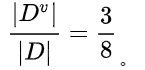
同时,在这三个样本中,工作都是好。
所以:
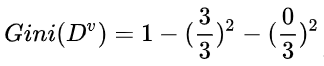
就有了加号左边的式子:
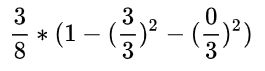
同理,当工资=0时,有5个样本,在这五个样本中,工作有3个是不好,2个是好。
就有了加号右边的式子:
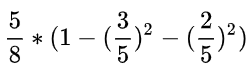
同理,可得压力的基尼指数如下:
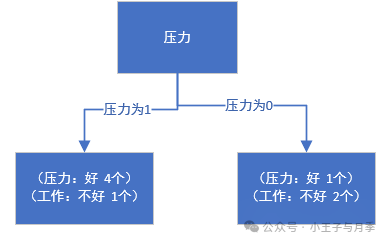
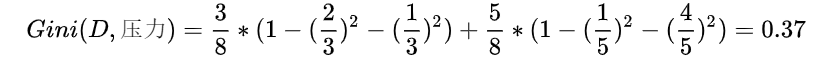
平台的基尼指数如下:
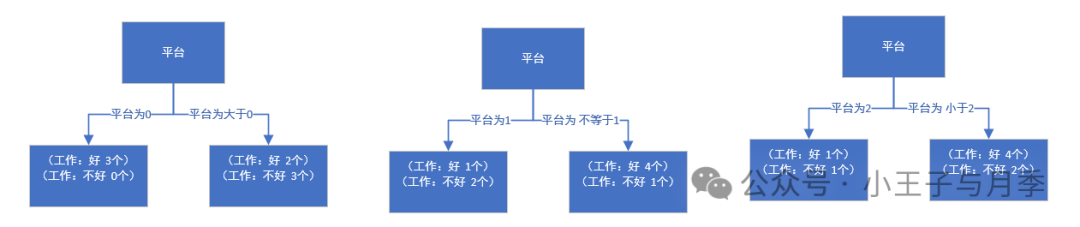
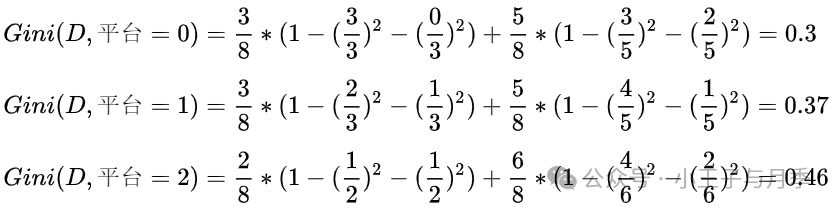
注意啦,在计算时,工资和平台的计算方式有明显的不同。因为工资只有两个取值0和1,而平台有三个取值0,1,2。所以在计算时,需要将平台的每一个取值都单独进行计算。比如:当平台=0时,将数据集分为两部分,第一部分是平台等于0,第二部分是平台大于0。
根据基尼指数最小准则,我们优先选择工资或者平台=0作为D的第一特征。
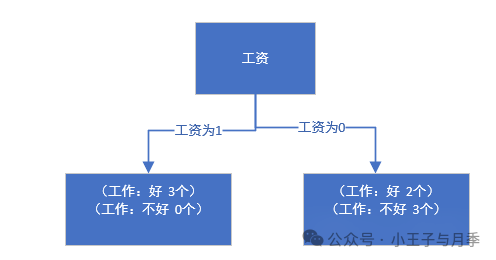
我们选择工资作为第一特征,那么当工资=1时,工作=好,无需继续划分。
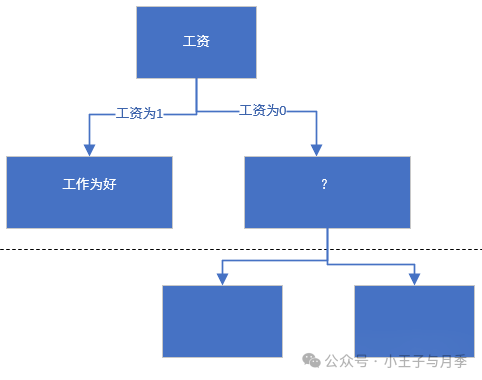
当工资=0时,需要继续划分。当工资=0时,继续计算基尼指数:
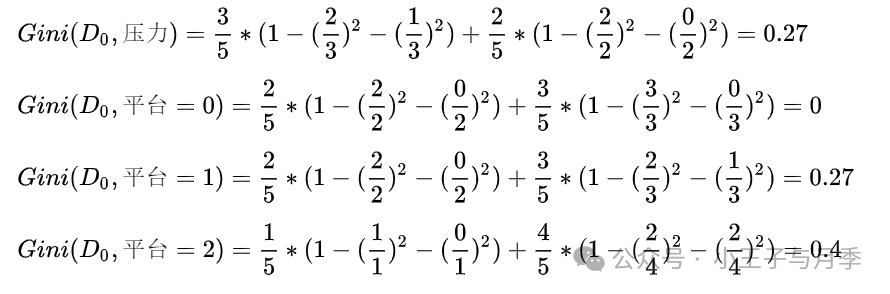
当平台=0时,基尼指数=0,可以优先选择。
同时,当平台=0时,工作都是好,无需继续划分,当平台=1,2时,工作都是不好,也无需继续划分。直接把1,2放到树的一个结点就可以。最终的决策树如下:
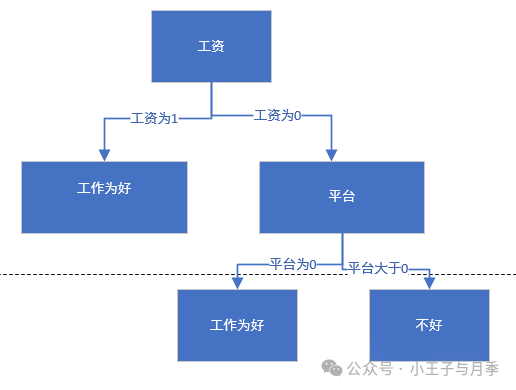
2. ID3(Iterative Dichotomiser 3)
ID3采用香浓的信息熵来计算特征的区分度。选择熵减少程度最大的特征来划分数据,也就是“最大信息熵增益”原则。它的核心思想是以信息增益作为分裂属性选取的依据。
处理问题类型:多分类
结构:多叉树结构
计算指标:信息增益
特点:简单易懂,无法剪枝、容易过拟合,无法处理连续值
存在的缺陷:该算法未考虑如何处理连续属性、属性缺失以及噪声等问题。
下面来介绍两个与此有关的概念:
信息熵是一种信息的度量方式,表示信息的混乱程度,也就是说:信息越有序,信息熵越低。举个列子:火柴有序放在火柴盒里,熵值很低,相反,熵值很高。它的公式如下:
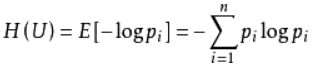
信息增益: 在划分数据集前后信息发生的变化称为信息增益,信息增益越大,确定性越强。
我们来看看代表之一 —— ID3算法。
在划分数据集之前之后信息发生的变化称为信息增益,知道如何计算信息增益,我们就可以计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
这里又引入了另一个概念——熵。这里先不展开说了,我们记住他的概念:一个事情它的随机性越大就越难预测。
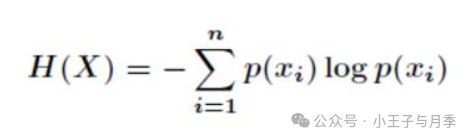
具体来说这个概率p越小,最后熵就越大(也就是信息量越大),如果极端情况一件事情概率为1,它的熵就变成0了。
比如,你如果能预测一个彩票的中奖号码就发达了。但是,如果你能预测明天太阳从东边升起来则毫无价值。这样衡量一个信息价值的事,就可以由熵来表示。
聪明的你或许已经发现了,决策树算法其实就是为了找到能够迅速使熵变小,直至熵为0的那条路径,这就是信息增益的那条路。我们将对每个特征划分数据集的结果计算一次信息熵,然后判断按照哪个特征划分数据集是最好的划分方式。
举个容易理解的例子:
解决问题:预设4个自变量:天气、温度、湿度、风速,预测学校会不会举办运动会?
步骤一:假设我们记录了某个学校14届校运会按时举行或取消的记录,举行或者取消的概率分别为:9/14、5/14,那么它的信息熵,这里也叫先验熵,为:
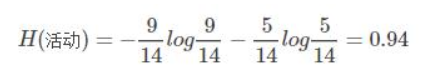
步骤二:我们同时记录了当天的天气情况,发现天气好坏和校运会举行还是取消有关。14天中,5次晴天(2次举行、3次取消)、5次雨天(3次举行、2次取消)、4次阴天(4次举行)。相对应的晴天、阴天、雨天的后验熵。

步骤三:我们计算知道天气情况后的条件熵。
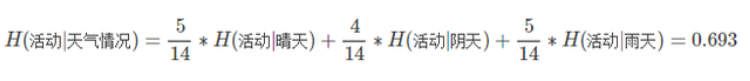
步骤四:我们计算在有没有天气情况这个条件前后的信息增益就是。
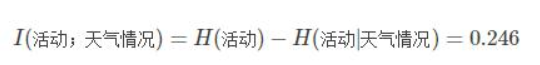
步骤五:我们依次计算在有没有温度、湿度、风速条件前后的信息增益。
步骤六:根据设置的阈值,若信息增益的值大于设置的阈值,选取为我们的特征值,也就是我们上图中的矩形节点。
步骤七:生成决策树。选取信息增益最大的自变量作为根节点。其他的特征值依次选取为内部节点。
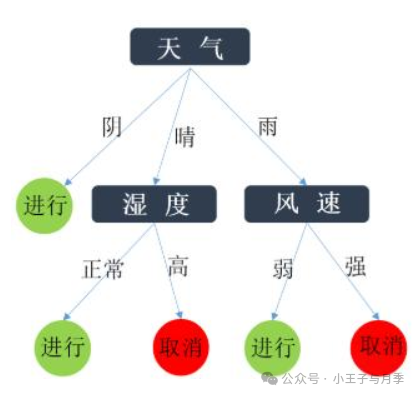
比如上面的例子是这样的过程:

经过如上步骤,我们得到决策树。可以看到,最终们只选取了3个特征值作为内部节点。
3. C4.5
J.R.Quinlan针对ID3算法的不足设计了C4.5算法,引入信息增益率的概念。它克服了ID3算法无法处理属性缺失和连续属性的问题,并且引入了优化决策树的剪枝方法,使算法更高效,适用性更强。
处理问题类型:多分类
结构:多叉树结构
计算指标:信息增益
特点:可以处理缺失值,连续值,可以剪枝,避免过拟合
同样介绍一下信息增益率:在决策树分类问题中,即就是决策树在进行属性选择划分前和划分后的信息差值。
五、决策树的优势与局限是什么?
优势:
- 易于理解和解释,生成的决策规则可以直接转化为业务策略。
- 可处理分类问题及回归问题,分类问题可处理多分类问题。
局限:
- 容易过拟合。决策树倾向于生成复杂的模型,容易过拟合训练数据,导致模型在新数据上的性能下降,缺乏泛化能力。为了解决这个问题,可以通过剪枝、限制树的最大深度或引入正则化等技术来控制模型复杂度。
- 对噪声及不均衡数据非常敏感。噪声数据可能导致错误的分割点,从而影响模型的准确性。在不均衡数据集中,如果某个类别的样本数目远远超过其他类别,则决策树往往倾向于选择该类别作为划分点,造成模型偏向该类别。
- 对输入数据的微小变化敏感,可能导致完全不同的决策树生成。
- 决策树计算复杂。决策树的构建过程中,需要对每个特征进行多次划分,并计算信息增益、基尼系数等指标。这导致了决策树算法的计算复杂度较高,特别是在处理大规模数据集时。为了降低计算负担,可以采用一些优化技术,如特征选择和剪枝。
六、 决策树的日常应用场景有哪些?
1. 信用评估
银行或金融机构在进行个人或企业信贷审批时,可以使用决策树模型根据申请人的特征(如年龄、收入水平、职业、负债情况等)来预测其违约风险,并据此制定贷款策略。
2. 市场营销
在市场细分中,公司可通过决策树分析客户的购买行为、消费习惯、地理位置等信息,以识别潜在的目标群体并定制营销策略。
3. 医疗诊断
构建疾病诊断模型,医生可以根据病人的症状、体检结果等因素快速得出可能的诊断结论,如心脏病发作的风险评估、肿瘤分类等。
4. 图像识别
虽然深度学习在图像识别方面表现优异,但在某些简单场景下,基于像素强度值或其他提取出的图像特征构建的决策树或随机森林也能实现有效分类,比如医学影像中的结节检测。
5. 推荐系统
用于基于内容的推荐,根据用户的属性和历史行为数据建立模型,决定向用户推荐何种类型的商品或服务。
参考:
作者:厚谦,公众号:小王子与月季
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
