匹配策略:为什么打车软件不给你最近的车?
好久没有更新,最近大出行领域风起云涌,那么就趁着这个机会简单聊一下打车的匹配策略。
本身服务匹配算法是非常复杂的,要考虑多个因素,但是如果我们只看最基本的逻辑,服务匹配就是将多个服务者和多个用户之间进行匹配。这篇文章会简单介绍如何构建匹配度,同时具体如何对匹配问题求解。
1. 匹配度构建
匹配度的构建其实并不复杂,就是构造一个计算用户需求和服务者之间的相关性的方法。复杂的是确认清楚我们的目标是什么。介绍核心函数的构建我们仍然以打车为例。
比如在打车的时候,我们可以先思考下有哪些因素是乘客叫车的时候乘客比较关心的。首先乘客最关心的就是司机和乘客之间的距离。对于每个乘客而言,距离越近就意味着司机赶过来越快,等待时间越短,在大多数情况下,快速上车出发是乘客的第一需求。乘客关心的第二个问题是司机的服务,具体体现在乘客对于司机的评价和司机的服务单量上,用户评分越高的司机往往更能提供优质的服务,如果可以周围有大量司机可以选择的话,乘客期待评分更好的司机。对于司机而言,司机期待乘客的终点是热点地区,这样可以获得更高的收入,如果周围有大量的乘客,那么单纯从效率的角度看,我们更应该匹配目的地在时空价值更高时间域的订单。如果业务取向真的是上面分析的这样,那么用户和司机的匹配度函数就应该由三个因子构而成。不过当多个参数在同一个函数中的时候,就需要对每个参数进行有效的归一化和变形,才能让结果符合预期。
需要强调的一点是,当我们对每个用户和周围的司机都有相关度计算,可以知道对每个用户最合适的司机,也并不意味着所有用户都可以得到最合适的司机。这就回到了一个用户经常抱怨的问题:为什么打车软件不给我派最近的车?
即使核心函数中只有距离一个因子,也不一定会给每个用户都匹配最近的车。具体case如下图所示: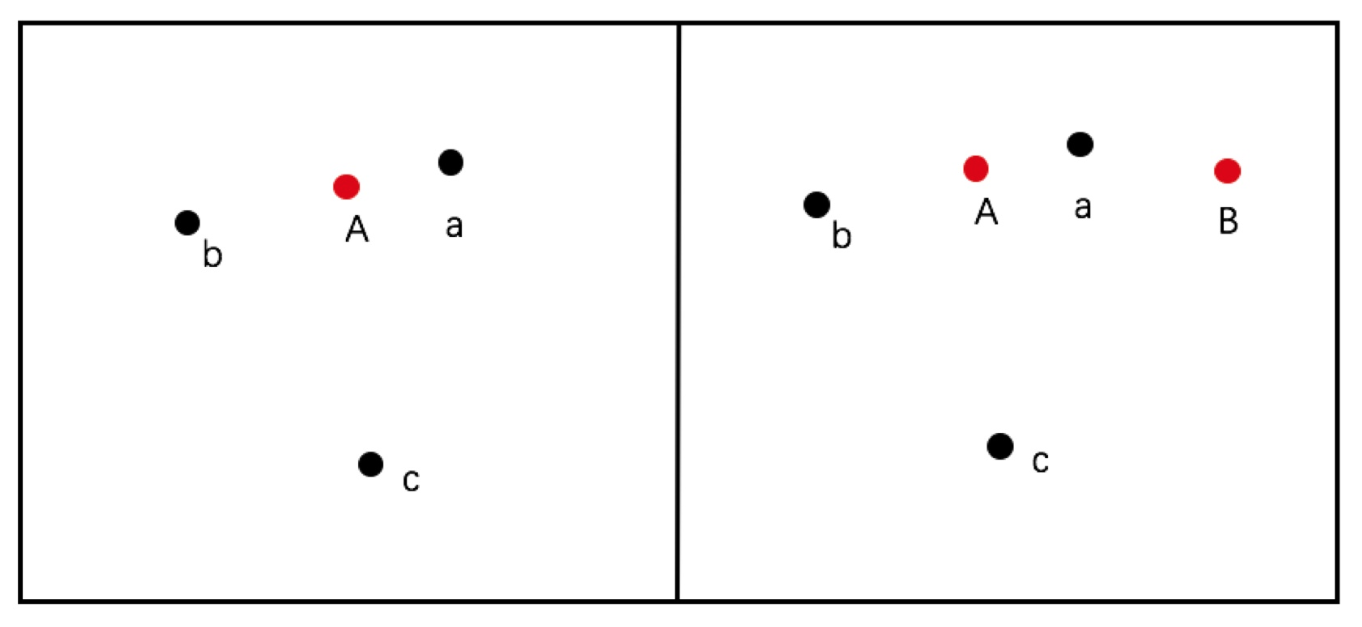
在左边的图中,距离用户A最近的车是a,在这种情况下可以给用户A派最近的车。但是如果如右边图所示,同时有两个用户呼叫,这种情况下,给用户A分配车辆a,会导致B分配到的车都会比较远。就应该给用户A分配车辆b,给用户B分配车辆a。而实际在设计的服务匹配方法中还需要考虑多种其他因素,比如服务、公平等因素,就更不可能给所有用户都分配最近的车。
从这个例子中看出,系统应该寻求的是整个系统匹配度最大化。下面我们会详细阐述可以用什么样的方法来达到系统的最优化。
2. 二分图匹配
二分图是图论中的一种特殊模型。 通俗解释的话,二分图有两个特点,在二分图图中的点可以分到两个互不相交的子集中,同时每条边都需要连接这两个子集。如果有这个定义去看的话,一段时间内,乘客和司机的匹配问题就是典型的二分图问题,两个集合分别代表司机和乘客,司机和乘客的匹配度则代表司机的边长。
在二分图中,有一个经典问题就是如何求二分图的最大匹配。最大匹配的定义就是任意交点只连接一条边的最优解。具体到打车问题中,就是寻找让整个系统叫做多的人叫到车,所有人和司机之前的匹配度之和最大。这也正是我们希望得到的线下交易系统最好的匹配结果。如果我们能找到二分图的最大匹配算法,就能用这个算法作为线下交易匹配的问题。
值得庆幸的是二分图问题是有典型的求最大匹配的算法的。二分图问题本质上也是线性规划问题,用线性规划的单纯形法也可以作为迭代方法。不过因为这种方法效率低下,工程上不会使用。在工程上使用最大流、匈牙利算法或者KM算法都可以作为最大匹配问题的解法,尤其是KM算法基本就是为了解决二分图这种特殊问题设计的算法。这三种算法在效率和原理上是基本通用的,这里涉及一些基础图论问题,就不对这些算法做数学展开,有兴趣的读者可以从网上查找KM算法相关资料。
当然,即使不了解KM算法的数学原理,但是并不妨碍我们理解使用这种方法。KM算法要求的两个集合中的不同点的匹配度作为边长,权重越大则代表匹配度越高。算法通过迭代会给出匹配度最高的匹配组合,也就是我们需要的全局最优解。在KM算法中,只要将所有我们需要的因素都考虑进入匹配度算法中,那么这个算法就可以每隔一段(比如10s)时间执行一次,每次服务者和用户退出匹配系统,也会有新的服务者和用户加入匹配系统,算法循环执行,不断匹配。
3. 给太长不看的朋友
打车的匹配策略就和男生和女生相亲一样。为什么不给所有男生自己最喜欢的女生,因为资源有限,一个女生也不能分给一堆男生。那么最好的结果就是每个人都找到差不多和自己匹配的人,让整个系统成双入对的情侣满意度总和最高。
那么回到打车的问题,为什么不给你最近的车,因为同时有一堆人想要最近的车,系统不能保证给每个人最近的车。那么最终系统的优化目标就变成了最大化整体的效率和体验指标。不给一个特定最近用户最近的车,是因为对于系统而言,最优化的目标是系统的最优化,不是针对每个人的最优化。
作者
潘一鸣,知乎专栏:产品逻辑之美。THU/PM,关于产品,除了概念和界面,还能聊些别的
关键字:匹配策略, 打车软件, 匹配, 算法
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
