做问卷调查时，你真的会选择样本吗？

一、抽样框

抽样框在抽样调查中处于基础地位，是抽样问卷调查必不可少的部分，其对于推断总体具有相当大的影响。

抽样框是用来代表总体，从中抽选样本的一个框架。具体表现形式可以是一个学生的花名册、工商企业名录等。例如：假设现在要调查全国32万所小学的学生家长对于国家“双减政策”的民意调查，从中选取出10所最具有代表性的小学，并从中抽取出10000名学生家长进行调查。

那么在这个例子中 ，总体是32万所小学的学生家长，抽样框是所选出的10所小学的学生家长名册，样本是最后抽取出的10000名学生家长。

当然抽样框也不定是具象的，也可能是抽象的，例如，在大型零售商场对购买者或消费者进行随机访问调查时，并没有具体的名册。

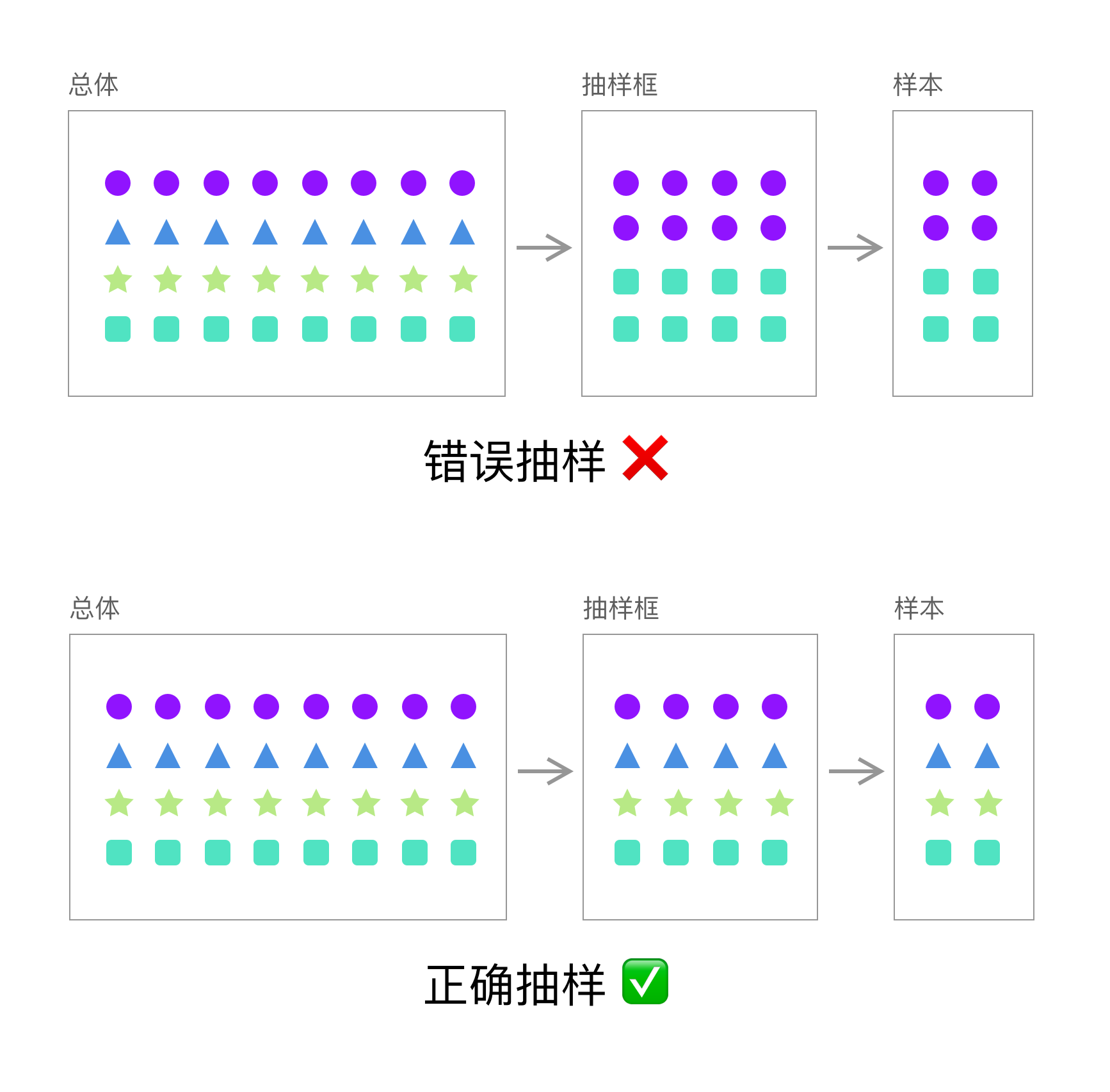
抽样框选取能否代表总体，直接决定了调研结果的可靠性。在我们的例子中选取10所学校家长需要能够代表全国32万所学校的学生家长，需要考虑的因素有很多，比如：收入因素、地域因素、宗教因素等等，因此在调研初期，根据调研的目的和主题尽可能确定准确的抽样框，从而减少调查的误差。

我们来看一个由于抽样框选取错误，而导致失败的案例：1936年美国总统选举民意测验。

1936年美国总统大选，竞选的是民主党的罗斯福和共和党的兰登。美国权威的《文学摘要》杂志社，为了预测总统候选人谁能当选，采用了大规模的模拟选举（他们以电话簿上的地址和俱车辆注册系统的地址发出1000万封信，收到回信200万封）。预测兰登将以57%对43%的比例获胜，并大力进行宣传。

最后选举结果却是罗斯福以62%对38%的巨大优势获胜。原因是在1936年的美国，富裕的家庭才有私人电话和汽车。为了挽救大萧条造成的经济打击，当时的罗斯福政府强行干预市场经济，从而在富人中普遍缺乏好感。

因此，《文学摘要》的调查样本不是从总体（全体美国选民）中随机地抽取，而是主要从富人的抽样框中抽取，这样的调查结果当然对罗斯福不利。

在问卷领域，最关注的是“代表性”，而非数量。因此在选取样本框时，一定要从多方面因素来考虑，从而避免选取出误差较大的样本框。

也许你想问，怎么才能知道自己的样本数据是否正确。 很遗憾的告诉你，没有办法，除非调查了全部的总体，才能准确的知道自己抽取的样本是否正确。 但是没有关系，误差是会永远存在的，我们需要做的是尽可能的减少误差，而不是消灭误差。

二、抽样方法

抽样是指从抽样框或总体中抽取出一部分数据作为样本的动作。抽样的方法有很多，介绍几种常见的抽样方法。

1. 简单随机抽样

一般的，设一个总体个数为N，如果通过逐个抽取的方法抽取一个样本，且每次抽取时，每个个体被抽到的概率相等，这样的抽样方法为简单随机抽样。适用于总体个数较少的。

2. 系统抽样

当总体的个数比较多的时候，首先把总体分成均衡的几部分，然后按照预先定的规则，从每一个部分中抽取一些个体，得到所需要的样本，这样的抽样方法叫做系统抽样。

3. 分层抽样

抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层中独立抽取一定数量的个体，得到所需样本，这样的抽样方法为分层抽样。适用于总体由差异明显的几部分组成。

4. 整群抽样

整群抽样又称聚类抽样。是将总体中各单位归并成若干个互不交叉、互不重复的集合，称之为群；然后以群为抽样单位抽取样本的一种抽样方式。应用整群抽样时，要求各群有较好的代表性，即群内各单位的差异要大，群间差异要小。

5. 多段抽样

多段随机抽样，就是把从调查总体中抽取样本的过程，分成两个或两个以上阶段进行的抽样方法。

系统、分层、整体、多段比较难实现，在问卷调查中经常被使用到的方法是简单随机抽样。

三、如何确定最小取样数量

样本量越大越好吗？样本量确实越大越好，样本越大越接近数据总体情况，但样本量越大同时也代表需要付出更多的人力和财力，所以往往出于现实因素的考虑，需要确定最少取样数量。最小取样数量公式如下：

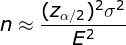
n：样本量

?^{2}：方差（用来衡量数据离散程度：?^{2}=\frac{∑(X-μ)^{2}}{N}

X：变量

μ：总体均值

N：总体例数

在调研实际情况中，往往方差都是未知的，所以在这种情况下可用样本率进行预估，当样本率P=0.5时，P(1-P)=0.25，此时为方差理论最大值。

Z_{?/2}：置信度（用来表示估计结果的可靠性）当置信度为95%时，Z_{?/2}=1.96；当置信度为90%时，Z_{?/2}=1.64（其他数值的置信度可以通过正态分布表/t分布表中查到）

E：抽样误差（用来表示可接受的抽样误差）

根据最小样本的计算公式我们可知样本量的大小不取决于总体的多少，而取决于研究对象的变化、所要求或允许的误差大小，以及要求推断的置信程度。

举例：当你希望的调查结果要达到90%可靠程度，且误差不超过2%，那么需要的样本约等于\frac{1.64^{2}\times0.25}{0.02^{2}}=1681个。从统计学角度，在要求的精准度水平下，不考虑其他的因素影响，若简单随机抽样，300～400个样本已经能够达到置信度95%，误差率不超过5%。

需要一提的是，当样本低于100时，几乎所有的结构方程模型分析都是不稳定的，大于200以上的样本，才称得上一个中型样本。若要得到稳定的结构方程模型结构，低于200的样本数量是不鼓励的。

作者：WOWdesign，研究设计价值最大化，涉及用户体验、品牌体验、空间体验。

本文作者 @WOWdesign 。

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！