经典腾讯面试题:小白鼠试毒问题
这是一道非常经典的腾讯面试题,可能对于程序猿来说并不陌生,但是对于第一次看到这道题的同学来说,确实会比较烧脑。今天除了讲解这道题如何解,更多的是希望给大家引入信息论的概念,那么以后不管是遇到试毒药还是称球重这类问题,都是小case啦!

可能有人会说,我用100只小白鼠就可以知道毒药是哪瓶了,所以小白鼠是招你还是惹你了,非要搭上一整个家族来给你找毒药?其实这个问题答案很简单,我们只需要7只小白鼠就够了,而这个问题的解题关键就是数学编码中的二进制。
一、如何用7只小白鼠找毒药 — 二进制编码
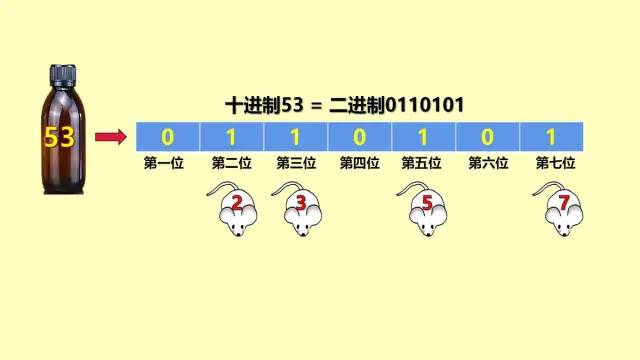
Step1:我们对100个瓶子进行1~100号的编码,再转化为7位的二进制码(至于为什么是7位,看到后面你就懂了)。比如1号瓶子就转化为了“0000001”,10号瓶子就转化为了“0001010”:

Step2:找来7只小白鼠,分别对他们进行1~7的编号。对于编号是1的小白鼠,喂它所有二进制编码第1位(从左到右数)为1的瓶子;对于编号2的小白鼠,喂它所有二进制编码第2位(从左到右数)为1的瓶子;以此类推…
Step3:接下来就是看一天后哪几只老鼠挂了:如果某个编号的老鼠死了,那说明毒药瓶子的二进制编码在对应编号位置上的二进制值是1;反之如果某个编码的老鼠没有死,那说明毒药瓶子的二进制编码在对应编号位置上的二进制值是0。假如最后是2,3,5,7号老鼠挂了,那说明对应的毒药瓶子二进制编码是“0110101”,转化成十进制,即第53号瓶子是毒药。
二、为什么至少是7只小白鼠?— 信息熵
前面我们只说明了7只小白鼠是可以完成找毒药这件事情,但是我们并没有证明7只就是最优解,那要论证这个答案就要引入信息论中的“信息熵”这样一个概念。
首先,我们先来了解下“熵”:
在信息论中,熵的概念和热力学中的熵是类似的,如果大家还记得高中化学,里面有提到一个“混乱度”的概念,其实熵在热力学里指的就是系统的混乱度,大概应该还记得“任何化学变化或者化学反应都是往熵增加的这个方向进行”这句话吧。
热力学熵:系统的混乱程度
信息熵:信息的不确定性的度量
而在信息论中,熵指的是信息的不确定性,也就是说信息的不确定程度越大,那么对应的信息熵的也就越大,其实数学的本质就是消除信息中的这种不确定性。
对于抛硬币来说,每次要猜正反面只能靠瞎猜,正反面出现的概率都是1/2,对于这类事件来说其不确定性较大,信息熵也会相对较大;如果让你猜国足拿世界杯冠军的可能性,那这种小概率事件的不确定性就比较小了,信息熵相对来说就会很小。
在信息论中,常用的几个概念也可以给大家定义下,避免混淆:
1、信息熵:用来度量信息不确定性程度的大小,是一个绝对的值。(至于具体怎么计算度量,后面介绍)
2、信息:凡是在一种情况下能减少信息的不确定性的任何事物,都可以叫信息,它的反义词可以理解为是“废话”
3、信息量:是对信息的度量,表示某个具体事情发生后带来的信息的多少,是个相对值。事件发生的概率越低,当事件发生了以后带来的信息越大,说明信息量越大;反之越高概率事件的发生,其产生的信息量就越小。比如某明星出轨的消息被爆出来,而之前他在大众面前的人设是个极品好男人,那么这则消息的信息量就非常大了。
接下来,回到“信息熵”如何计算度量:
信息量度量的是一个具体事件发生了所带来的信息,而熵则是在结果出来之前对可能产生的信息量的期望——考虑该随机变量的所有可能取值,即所有可能发生事件所带来的信息量的期望。
所以香农给了我们一个这样的公式(划重点!):

P为X的概率质量函数(probability mass function),我们可以理解为事件xi 发生的概率。
b是对数所使用的底。当b = 2,熵的单位是bit。
我们用抛硬币来举例,“抛一次硬币是正面”这个随机变量X的信息熵为
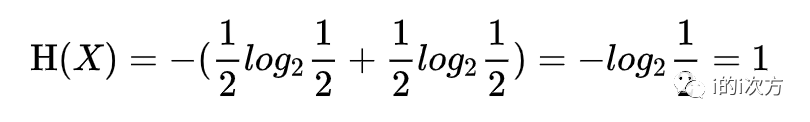
也就是“抛一次硬币是正面”这个事件的信息熵是1 bit,我们也就只需要用1位二进制的数字即可以表示这个信息的大小(0或者1)
#开始解题# 计算小白鼠找毒药中的信息熵:
1、首先,”100瓶药水其中有1瓶有毒“这个随机变量X的信息熵为:

2、1只小白鼠喝水以后的要么活着,要么死去,一共有两种状态,所以”1只小白鼠喝完水以后的状态“这个随机变量Y的信息熵为:

3、n只小白鼠喝完水会有2^n种状态,即”n只小白鼠喝完水以后的状态”这个随机变量Z的信息熵为:
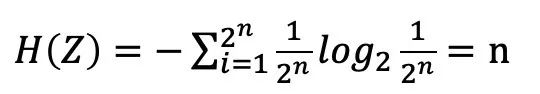
所以根据题目,要用到最少的老鼠来找到那瓶毒药,转化为信息熵就是要满足:
H(Z) >= H(X),即n >= 6.64
那么n的最小值是7,也就是说最少要7只老鼠可以找到毒药
其实,上面的熵计算如果你觉得复杂的话,也可以这么简化来理解:
1只小白鼠活着或者死了,可以代表两种状态,n只小白鼠就代表2^n种状态
而毒药存在1~100号瓶子中的某一瓶对应了100种情况
也就是我们需要找到最小的n满足:
2^n>= 100,即n>=7
三、挑战下高阶版的试毒问题

仔细审题,我们发现这次小白鼠6小时内就会挂掉,题目没有说具体是什么时候会挂,那我们可以理解为:喝了毒药最久6小时会挂,如果6个小时还没挂,说明这瓶水不是毒药。
1、首先,还是”100瓶药水其中有1瓶有毒“这个随机变量X的信息熵为:

2、而这次,小白鼠的状态有点不一样,他在喝完水1天内的状态可能是:
1)在第0分钟的时候喝了一滴水以后,第6小时死去
2)第6小时依然活着,喝了一滴水以后,第12小时死去
3)第12小时依然活着,喝了一滴水以后,第18小时死去
4)第18小时依然活着,喝了一滴水以后,第24小时死去
5)第6小时依然活着,喝了一滴水以后,在第24小时依然活着
可见一只小白鼠在喝了一整天水后,可能会出现的状态有5种,所以”1只小白鼠喝完水24h以后的状态“这个随机变量Y的信息熵为:
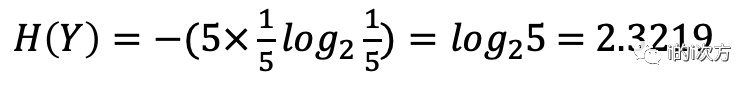
3、n只小白鼠喝了一整天水后就会有5^n种状态,即”n只小白鼠喝完水24h以后的状态”这个随机变量Z的信息熵为:
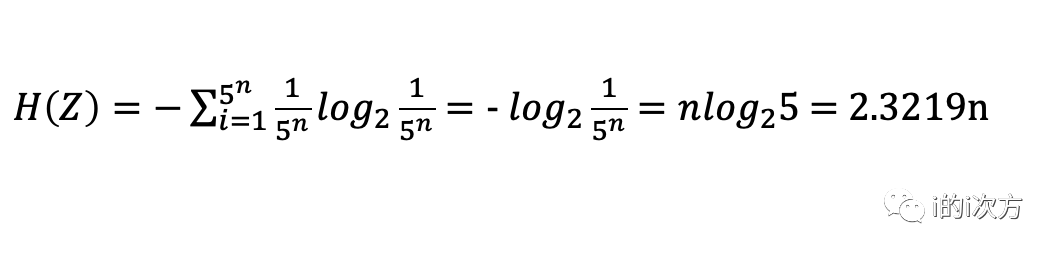
所以根据题目,要用到最少的老鼠来找到那瓶毒药,转化为信息熵就是要满足:
H(Z) >= H(X),即 2.3219n >= 6.64
那么n的最小值是3,也就是说最少要3只老鼠可以找到毒药
留个作业:那具体怎么利用这3只小白鼠找到毒药呢?
根据前面简化版本的二进制编码方式的思路,我们是不是可以利用小白鼠的5种状态构造一个5进制编码方式呢?
四、我是总结
其实小白鼠试毒这个问题,第一次遇到确实会比较难下手,对于做过的人来说,可能大部分人也仅仅停留在知道用二进制编码的方式解决,很少会有人去思考这背后的原理和逻辑的本质。
如果把问题变得再复杂点,往往大部分人就会去试,7只小白鼠不行就8只小白鼠,反正只知道用编码的方式,这就是知其然而不知所以然。同样的,当我们仅仅掌握了许多理论知识,但是缺乏应用场景的实操以及面向各种情况的修正与优化,最终也将是纸上谈兵。
所以,这也是我个人比较推崇的一种思考方式:当我们遇到一个好玩的问题以及巧妙的解决方法的时候,我们可以继续去深挖背后的原理和逻辑的本质,再反推更多的应用场景,做到举一反三,这样才能不断的锻炼自己思维能力的广度和深度。
本文作者 @WINTER
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
