线性回归算法：用“线性外推”的思路做预测

前两篇文章我们介绍了两个解决分类问题的算法：K近邻和朴素贝叶斯，今天我们一起来学习回归问题中最经典的线性回归（Linear Regression）算法。

一、基本原理

生活中，大家都排过队，我印象最深的应该是排队做核酸的队伍，前后间隔一米，随着做核酸的人越来越多，新来的人看到队伍，都会自动排到队伍的末尾，同样间隔一米，大家“齐心协力”排出了一条长线。

有了这条长线之后，我们就可以对新来的人排队的位置做出预测，这就是线性回归的基本逻辑。

所以线性回归算法的思路就是：根据已有的数据去寻找一条“直线”，让它尽可能的接近这些数据，再根据这条直线去预测新数据的结果。

那么具体要怎么找这条“直线”呢？初中数学里描述一条直线时，用的是一元一次方程：y=ax b，这里的a表示直线的斜率，b表示截距，如下图所示：

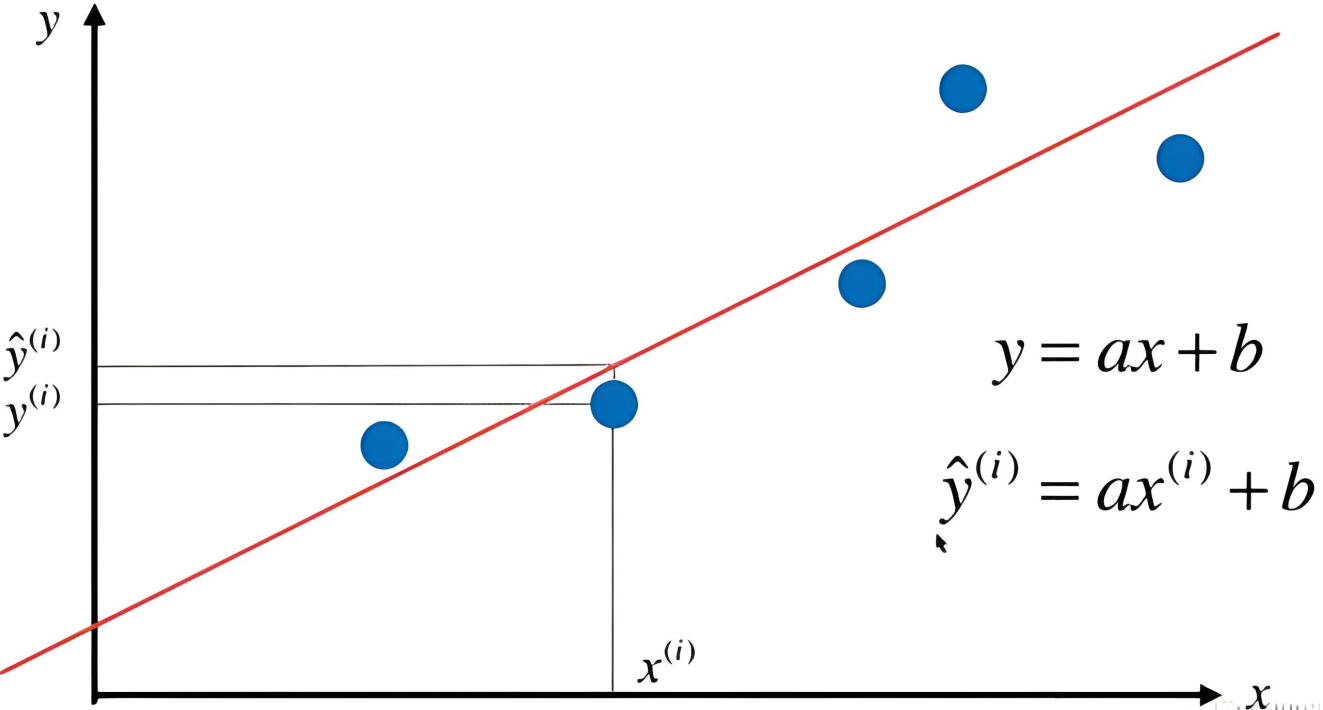
以排队为例，我们已知x是人的顺序，y是排的位置，将已有的x和y数据代入到公式中，可以得到一组合适a和b的值来描述这条直线，也就是我们找到了这条直线的分布。

排队的例子比较简单，只有一个x变量，在实际的应用中，会有很多个影响结果的变量，比如预测贷款额度时，会有工资、是否有房等变量，用线性回归的思路解决类似的问题，就要构建多元回归方程了，公式也就变成了 y = a1x1 a2x2 … b。

当有两个变量时，线性回归的分布也就不是一条简单的直线了，而是一个平面，如下图所示：

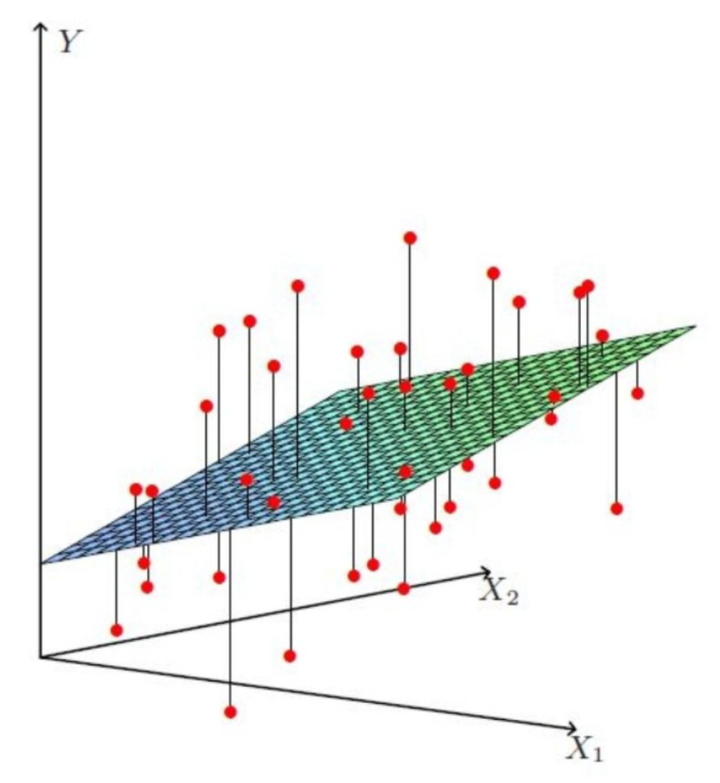
如果有更多的变量，分布就是一个超平面，找到它的分布也会变得更复杂。

二、如何计算最优解

如果每个人的站位（实际值）距离理想站位（预测值）的距离（误差）最小，那就说明我们得到的线性回归分布是最优解。

机器学习中，评价模型的预测值和实际值差异的公式叫做损失函数，损失函数值越小，模型性能越好。

平方残差和就是一种场景的损失函数，其计算公式为 loss=SUM（真实值-预测值）²，就是把每个节点的预测差求平方再求和，前面回归模型评估的文章里提到的MSE就是平方残差和除以样本数量。

三、应用场景

线性回归的应用场景非常广泛，只要数据是符合线性分布的，理论上都可以用线性回归来进行预测：

• 预测房价：通过分析房屋特征（如面积、位置、房间数量等）与价格之间的关系。
• 预测员工绩效：通过分析员工的教育背景、工作经验、培训等因素与绩效之间的关系。
• 营销分析：分析市场调研数据，预测产品销售量，并确定哪些因素对销售量有显著影响。
• 交通规划：预测交通流量，通过分析道路特征、人口密度等因素与交通流量之间的关系。
• 环境科学：分析环境数据，如气候变化、污染物排放等因素与生态系统的影响。

四、优缺点

线性回归算法的优点：

• 简单而直观：易于理解和解释，适用于初学者入门。
• 计算效率高：计算速度较快，适用于大规模数据集。
• 可解释性强：可以提供每个特征对目标变量的影响程度，有助于理解变量之间的关系。
• 可扩展性强：可以通过添加交互项、多项式特征等进行扩展，以适应更复杂的数据模式。

线性回归算法的缺点：

• 仅适用于线性关系：线性回归假设自变量与因变量之间存在线性关系，对于非线性关系的数据拟合效果较差。
• 对异常值敏感：线性回归对异常值较为敏感，异常值的存在可能会对模型的拟合产生较大影响。
• 忽略了特征之间的复杂关系：线性回归无法捕捉到特征之间的非线性、交互作用等复杂关系。
• 对多重共线性敏感：当自变量之间存在高度相关性时，线性回归模型的稳定性和可靠性可能会受到影响。

五、总结

本文我们介绍了线性回归算法的原理、应用场景和优缺点，线性回归是一个回归算法，常用来做预测值，和之前介绍的分类模型的输出是有区别的，需要注意一下。

下篇文章，我们来聊一聊逻辑回归算法，敬请期待。

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！