JZOJ 3441. 小喵喵的新家

Problem

Description

小喵喵和小聪聪从小就是好朋友 ，他们经常在一起玩耍 。如今小喵已经厌倦了自己居住的环境，想请小聪聪为她建一个新家。
小喵喵天生多才多艺，对多种乐器颇有研究。对于生活中常见的图形，她对圆形很感兴趣，因此小聪聪决定为她建一个圆形的新家。
我们设新家在一个平面直角坐标系上，其中新家的圆心为平面直角坐标系的原点。
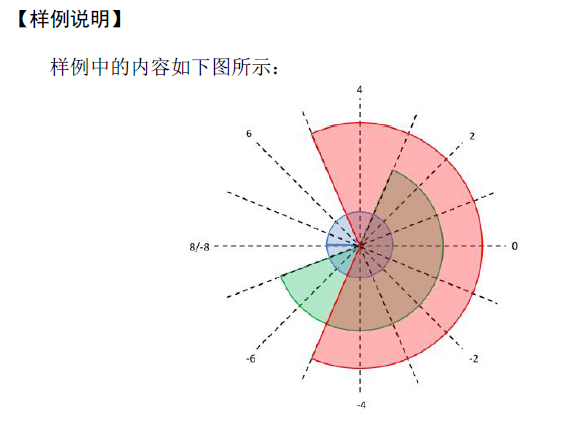
小聪聪有一把神奇的剪刀，他定义了一个值m，以等分 [−pi,pi]弧度 （详见样例）。他还有一支神奇的画笔，将进行 n次“铺地毯”操作。对于第i 次“铺地毯”操作，他将设定一个半径ri，起始位置si，终止位置ti ，然后从圆心角pi*si/m到圆心角pi*ti/m这部分区域逆时针铺上一个扇形地毯。
小喵喵想到了一个奇怪的问题，她想知道有多大面积被至少铺过k次地毯。 这个问题一下就难倒了聪明的小聪聪。 现在小聪聪求助于你，你能帮他解决这个问题吗？为了方便表达 ，设答案的值为T，你只需要输出 T×2m/pi的值即可 。

Input

第一行是三个整数 n，m，k，含义 如题目描述中所述。
接下来n行， 每行描述一次铺地毯操作 。第i行有三个整数r，si，ti，含义 如 题目描述中所述。

Output

输出 一个整数 表示T×2m/pi的值。

Sample Input

3 8 2
1 -8 8
3 -7 3
5 -5 5

Sample Output

76

Data Constraint

Hint

Solution

我们可以知道每一个扇形的面积为$\frac{ti-si}{2m}*\pi ri^2$,那么*2m/pi后，就剩下了$(ti-si)*r^2$.最简单的方法是一块块算面积，那么那一块的面积（合法的）为第k大的半径的平方（想一想为什么）。
那么如何实现呢？我们打一棵线段树，维护有几个扇形覆盖到了这块地方。如果我们要求第k大的数，那么我们要做一次搜索，初始值为k。

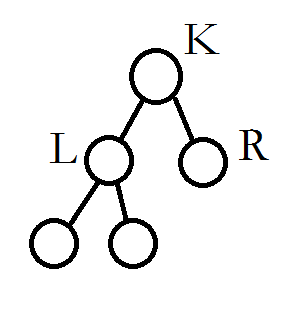
如果R>=K,则往右走，否则往左走，往左走的时候K-=R。走到最底的就是第k大的数的下标。
注意：如果si>ti,那么一个扇形将要变成两个扇形。从m/-m这条线这里割开。
——2016.7.6

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！