从实例出发，聊聊“平均值”和“辛普森悖论” | 白话数据分析

数据分析星球 2023-08-08 04:37:32

00 写在前面

不知道大家有没有类似的经历？有没有曾经因为追求高端的算法和工具而没有及时交付最终的业务结果，最后被老板一通批评；有没有拿着一个单点的数据分析结果就给出了一个全面的结论和建议；有没有给过一些因果倒置或者“幸存者偏差”的结论，导致业务走了弯路。这些经历大家多多少少都会遇到，为什么会犯这些错误？因为我们缺乏了一些基本的数据分析思维。

刚好最近一直在拜读郭炜的【数据分析思维课】，讲得很好，内容深入浅出，很接地气。我们很多人缺乏的不是数据分析的理论，而是在实际场景中应用理论的能力，理论+实际场景=方法论，如何把看似浮在空中的理论落地到实际的工作场景中来，就需要通过简单易懂的案例和近似白话的语言传达出来，这也是为什么会有【白话数据分析】这个系列的原因。

无论你是什么阶段什么水平，我们从生活/工作中最常见的案例出发，用最直白的文字把理论讲清楚，真正掌握数据分析的基本思维和原理，这也是写这个系列文章的初衷。

因为是白话，所以在这个系列文章中，没有晦涩难懂的公式和复杂的程序，我只是希望用大白话的形式，结合工作和生活中的各种各样的例子，学会怎样从数据分析的角度来解决这些问题，掌握一些数据分析最基本的知识。放我们再看待同一件事情的时候，思路和以前不一样了，可以从数据的角度来诠释身边发生的事情，用数据的思维来做出你的判断。

01 举个栗子

最近，公司的一位数据分析同事的竞品分析报告里提到：“我们客户的平均客单价是 100元钱，竞争对手的只有 50 元，我们的客户比对方的高端多了。所以我们产品要走高端路线”这些结论可信吗？还真不一定。

再举一个例子，某游戏公司做了款游戏，有 Android 和 iOS 版本。一个数据分析师看完用户的付费数据后，发现整体上 iOS 付费率比较高。他就直接告诉老板说，“我们 iOS的用户付费率要高于Android的用户付费率，我们应该集中资源开发iOS客户端！”这个结论可信么？还真不一定。

我们在日常生活中也会遇到这种情况，可以看到各种统计数据，“某市的人均住房面积是 120 平米”，“全国人均年收入超过 30 万元”，看完这个数据之后，开始怀疑人生了，对不起，我那么有钱我自己都不知道。

02 平均值为啥不靠谱？

以后看到这么不专业的统计报告就别看了。稍微有点数据思维的朋友都知道，这是我们被平均了，那准确客观的平均值统计应该是怎样的？

首先，我们得知道平均值究竟是什么。从概念上看，平均值有很多种。单从数学上来说，就有算术平均值、几何平均值、平方平均值、调和平均值、加权平均值等等。当然，我们日常生活中提到的平均值都默认是“算术平均值”，也就是“一组数据中所有数据之和再除以数据的个数”。

这个概念很简单，但是算术平均值有很大的短板，其容易受到极端值的影响而不能很好地表征整体水平。它无法客观准确地反映数据整体情况。更进一步来说，整体平均值是在数据呈均匀分布或者正态分布的情况下才会有意义，如果忽略整个数据的分布情况，只提平均值，其实是没有意义的。

这也就是为什么你会在读一些统计分析报告时觉得自己不是“被加薪了”，就是“被幸福了”。

03 啥是辛普森悖论？

好，再回到刚才的问题，统计报告说人均年收入达到了30w元，你很容易就会想到这里面有些年薪很高的人拉高了整体水平，所以需要分开来看，这个时候就需要去看细分群体的平均值，比整体平均值更有意义。

整体平均值不能代表各细分群体情况，局部群体结论和整体平均值结论可能会背道而驰。这个现象就是数据分析中最常见的“辛普森悖论”，辛普森悖论是 1951 年由 E.H. 辛普森提出的，简单来讲就是在分组比较中都占优势的一方，有的时候在总评中反而是失势的一方。指局部的结论和整体的结论完全相反。

再举个例子说明一下，公司要对客服部的服务质量进行评估，我们发现无论是男生还是女生，一组的优秀客服比例都比二组好，但总体上一组的优秀客服比例却比二组低。

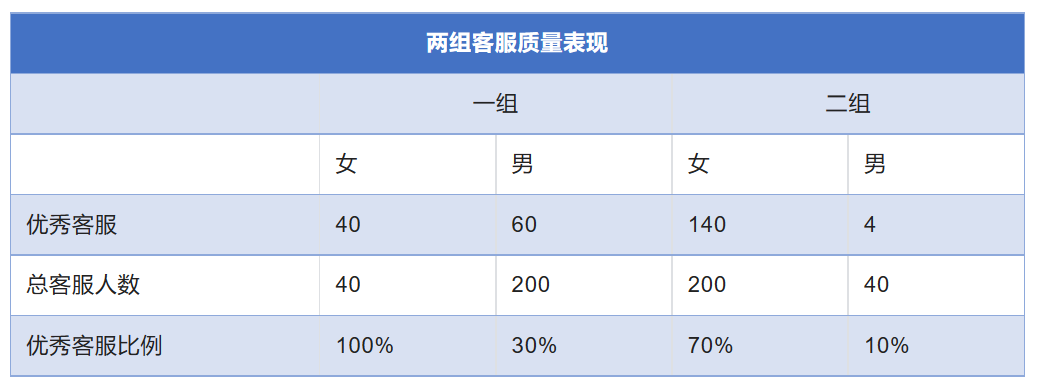
产品经理，产品经理网站

一组的优秀客服比例是：(40+60)/(60+200)≈40%
二组的优秀客服比例是:(140+4)/(200+40)=60%

二组的的整体优秀客服比例明显高于一组。再分开男女单独比较：

一组女生优秀客服比例100%，高于二组女生的70%。
一组男生优秀客服比例30%，高于二组男生生的10%。

一组的男生优秀客服比例和女生优秀客服比例都比二组高，但为什么一组整体优秀客服比例却比二组低？二组的优秀客服比例高的原因在于二组女生多，一组女生少，一组女生表现虽然好，但人数太少，拉不起整个一组的表现，导致二组整体成绩比一组好。细心的同学可能注意到了，这种悖论一般出现在分组样本不均衡的情况下，上面的例子中，两组男女性比例相差较大。

我们通常会讲到“质量”这个词，而且是一起出现，但实际上，“质”与“量”是两个不同的方面，我们在考虑质的时候，一定要注意量的影响，我们如果把这两者揉成一个“质”，就会出现辛普森悖论。

回顾一下文章开头提到的案例，我们发现Android用户的付费率比iOS用户低，再细分下去就会发现，我们也是错误地把“质”（付费率）和“量”（用户数）混为一谈，结论很有可能是错误的。

因为很有可能出现这样一种情况：Android 无论是男性还是女性的付费率分别都比 iOS 高，但是整体上因为Android男性用户比较多，而iOS女性用户比较多，简单一点可以理解为，Android以男性用户为主，iOS则恰巧相反，以女性用户为主，占据主导因素的Android男性的付费率比iOS女性的付费率要低，所以最终导致整体上Android用户的付费率比iOS用户低。

简单的道理来说，就是Android最大的优势（男性用户）没有比过iOS最大的优势（女性用户），这是决定最终整体走向的关键。