概率思维,人生真正的指南(上)
前言
我们每天都要做出各种决策。
一提到“决策”这个词,乍听起来可能不太接地气,会令人产生一种高大上的感觉。实际上,通俗地说,决策就是我们每天都要做出的各种选择。这样想来,可以毫不夸张地说,我们生活中的每个瞬间都离不开一系列决策。
有些是重大的决策,比如:决定自己未来职业方向、承担重要项目、决定重大投资等;有些是日常生活的选择,比如:是否要进行一个短期的旅行、今天晚上准备什么晚餐等,这些都需要我们做决策,但是如何才能做出合理的决策,对于每个人来说其实都是个挑战。
对这些需要在瞬间或短时做出决策的情形,你是否积累了足够丰富的应对策略呢?就算上升不到策略的高度,你至少也应该三思而后行,在充分思考的基础上,选择行动模式。
但是,在实际生活中,许多人肯定会不以为然,觉得根本没必要想得那么复杂,认为面对这些情形时全都只需要凭本能或者直觉做出决定。
这样做的结果就是人生往往会重复做出错误的判断。然而,总会有一些人能够持续做出比较合理的决策。他们有什么底层的逻辑和特殊的方法吗?
法国著名数学家拉普拉斯曾经说过:“人生中最重要的问题,在绝大多数情况下,实际上就只是概率问题。”从这个角度讲,概率才是人生真正的指南。
一、你真的了解自己的决策习惯吗
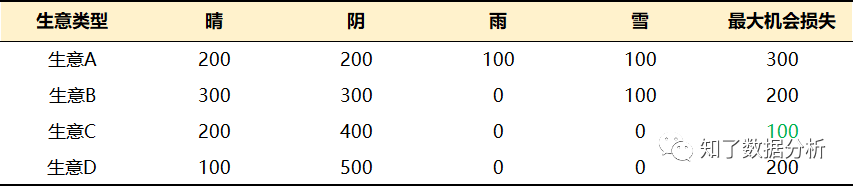
为了帮助大家能够更好的理解我们作出决策的底层逻辑,我们先来做一个小测试,希望大家能认真思考这个问题。通过对这些问题进行系统分析,大家可以从中发掘自己平时并不在意的一些决策习惯。请大家看下面这张表:
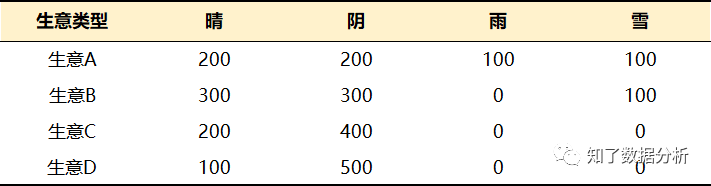
我们先介绍一下表中数据的相关情况。
假设下周的某一天,你需要在公园的露天环境下经营A、B、C、D四种生意。这些生意每天的销售额会受到当日天气状况的影响。通过表格,能够准确地掌握不同天气状况下经营各种生意当天获得的利润。
例如,经营生意A,如果天气是晴或阴,利润能够达到200元;如果天气是雨或雪,则利润只有100元。经营生意B、C、D同理。
那么,大家需要做的就是,在参考这个表格的基础上,从四种生意中选择你认为最合适的生意,并作出最终的决策。
关于选择,有一点需要特别注意,那就是除了表中提到的内容以外,再没有什么具有参考信息了。经营生意的公园没有具体的地理位置,不知道属于什么区域,可能在城市中心,可能在炎热的沙漠中,也可能在寒冷的雪国。不仅如此,关于具体的季节,也没有任何明确的信息。因此,大家要注意避免先入为主的错误倾向,不要根据自己目前所在的区域和季节等信息做出决策。
大家在深刻理解上述情况的前提下,从四种生意中选择一种,同时最好能认真思考一下自己做出选择的理由,一并记录下来。
实际上,关于这个调查并没有一个标准答案,它的真正意义也不是让大家选择所谓的“正确答案”。无论选择生意A、B、C、D中的哪一个选项,在某种意义上来看,全都可以算是“正确答案”。真正重要的是你做出选择的“依据”到底是什么。
下面,我将按照选项顺序,就选择四种生意所体现出的决策习惯进行分析。他们分别是:
- 考虑凡事做最坏打算的“最大最小准则”;
- 遵循二鸟在林,不如一鸟在手的“期望值准则”;
- 信奉搏一搏,单车变摩托的“最大最大准则”;
- 避免减了芝麻,丢了西瓜的“最小机会损失准则”
二、凡事做最坏打算
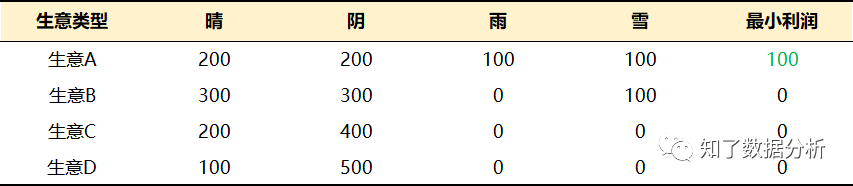
选择生意A的人往往存在着保底心理,他们认为做出这种选择“绝不会沦落到没有任何利润的境地”,也就是说“最少也可以有100元利润”。其他三种生意,都会受到天气状况的影响,存在没有利润的风险。这就是生意A与其他生意之间的差异所在。
因此,如果你基于“最少也可以有100元利润”的考虑,选择了生意A,那么就可以判断你的决策倾向带有“最少也能获得一些利润”的保守主义色彩。
从专业角度出发,这种决策方法被称为“最大最小准则(Max Min)”。其基本思路是小中取大,先找出各种情况下利润最少的情况,然后进行比较,从中选择利润最多的情况。
在追求某种利益或者冒险采取某种行动时,我们一般都会在脑海中想象最坏的局面,比如“最少也能保住本钱”,“最多也就承担这种程度的风险”,“想要告白,就算被拒绝,也只是伤心一会儿而已,并不会因此而变得一无所有”等。不管是有意识还是无意识,在日常生活中,我们每天都会做出类似的判断。因此,对于选择生意A的人,他们所依据的“最大最小准则”就非常自然地成了常用的判断准则。
对于“最大最小准则”,我们要注意,“究竟允许差到什么程度”的容忍度是非常重要的。在评价事物时,我们更倾向于给出1或0之类的定性结论,而不是连续地(一点点地)跟踪观察,比如“如果被逼降薪的话,我就辞职”,“如果再这么请假下去,就不给你学分”,“如果再磨磨蹭蹭,就别坐公共汽车去了”,“如果现在不结婚,不如就此分手算了”等。
在日常生活中,当必须做出这种非此即彼的判断时,我们自然要先考虑“究竟能容忍到什么程度”。所谓明确容忍限度是指明确“底线”。概括起来,“底线”是指“最小利益”或“最大风险”。
比如,选择生意A的情况下,最低收益为100元。换句话说,“不管发生什么情况(不管天气状况如何),必然会有至少100元的收益”。因此,我们也将100元称为生意A的保底值(security level)。这个数值是指采取某种行动后(或者未采取行动时),需要确保的最低利润值。有鉴于此,依据“最大最小准则”,我们应该选择保底值最大的行动方式。
其实在日常生活中,很多人都会应用这种思维方式。比如,在选择金融资产进行投资时,我们可能会无意间用到“最大最小准则”。
一般来说,股票属于风险资产,债券属于安全资产,尤其是国债。这是为什么呢?
这里,需要大家先明确一个概念,持有金融资产的利润主要包括两个方面——收入收益(income gain)和资本收益(capital gain)。
收入收益是指可以持续领取的现金收入;资本收益是指金融产品增值(转卖之后)带来的收益。股票的收入收益是企业拿出的分红,是以每股固定份额的形式共同分享的企业部分利润。债券的收入收益是事先约定好的利息。
不考虑资本收益,如果单纯对收入收益进行比较,就会发现股票是有风险的,而债券是相对安全的。这是因为股票的分红要受到企业业绩的影响,充满了不确定因素,而债券的利息是事先约定好的,相对稳定可靠。
也就是说,购买债券在绝大多数情况下可以拿到利息作为回报,其最小利润值是正数。与之相对,购买股票则可能面对零分红甚至亏本的风险。因此,从“最大最小准则”的视角出发,与购买股票相比,购买债券是更为合理的选择。
很明显,使用“最大最小准则”的优点在于不必过多考虑各种情况。无论是客观上还是主观上,都不用在意如何取分布概率。实际上,分布概率本身是非常烦琐的。从某种意义上讲,如果可以规避这个环节,那将是一种非常经济实惠的做法。
如果再往深一点看,使用“最大最小准则”甚至于不用再逐个思考各种基本事件了。比如在追求利润的情况下,除了利润最小的情况以外,只要认定“所获利润比最小利润大”,就不用再去认真考虑“具体大多少”的问题了。这样一来,就可以大幅削减由于思考而耗费的时间和精力。
但是,从另一个角度来看,这里列举的优点可能也是缺点所在。“最大最小准则”是一种过于保守的准则。不管怎样,这种准则将关注的焦点全部集中在了最差局面上,根本不在乎除此以外的其他利润(或损失)。因此,可以说,这是一种片面的、极端的判断。
比如有两种彩票,一种是“99%的情况下可以中100万元,1%的情况下只能中1万元”,另一种是“99%的情况下可以中3万元,1%的情况下只能中2万元”。
如果依照“最大最小准则”,我们应该选择后者,因为前者的保底值是1万元,后者的保底值是2万元。然而,如果冷静地思考一下,你就会发现“选择前者的话有很大概率可以获得100万元的收益,而选择后者的话最多只能获得3万元的收益”,这才是更为合理的逻辑。之所以选择前者,是因为担心出现发生概率极低的最差局面:只拿到1万元的收益。但就是因为做出这种选择,才忽视了有很大概率可以获得的100万元的收益。
此外,如果完全根据“最大最小准则”做出判断,就会出现“无论如何也不会乘坐可能发生死亡事故的交通工具”的情况。在这种情况下,人们会丧失理性思考的能力,根本不去求证乘坐交通工具导致死亡事故的概率到底有多大,而是彻底放弃乘坐交通工具。
所以,根据这种准则,很容易陷入到一种偏激的思维中。
三、二鸟在林,不如一鸟在手
选择生意B的人认为,“在四种天气状况下的利润之和中,生意B的数值是最大的”。实际上,如果将生意B在各种天气状况下的利润加在一起是700元(300+300+0+100)。与之相对,生意A、生意C和生意D在各种天气状况下的利润之和分别为600元(200+200+100+100)、600元(200+400+0+0)和600元(100+500+0+0)。也就是说,生意A、生意C和生意D的利润都是600元,均小于生意B的利润。
那么,这种“将所有可能实现的利润加在一起”的做法究竟有什么意义呢?为了更加清晰地说明这一点,需要进行一些深入的讨论。在此,我希望通过下述方式简单进行解释,帮助大家有一个更为直观的认识。
如果你能够拥有四次机会,分别在四种不同的天气状况下经营生意。那么,你所得的总利润就应该是四次经营生意所获利润相加之和。在这种“分别尝试全部可能性”的“等概率准则”指导下,你选择生意B是完全合情合理的。
由于实际上你只有一次机会做选择,因此我们就选择更为简单直接的思维方式,也就是“单纯对四种天气状况下经营生意的利润进行平均”。在这种情况下,单纯平均就是求四种天气状况下经营生意的利润之和的平均值,也就是用利润之和除以4。按照这种算法,生意B的利润平均值是175元(700÷4),而其他三种生意的平均值是150元(600÷4)。
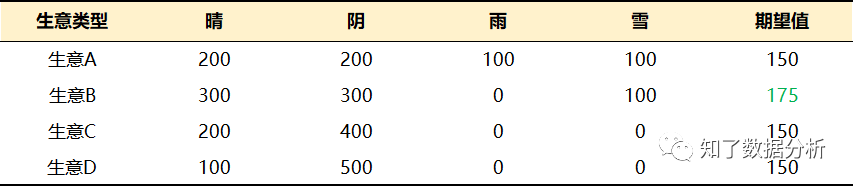
如果用一句话来概括,我们可以认为选择生意B的人“单纯对四种天气状况下经营生意的利润平均值进行了比较,并选择了其中最大的数值”。人们将这个平均值称为“期望值”。因此,选择生意B的决策方法又被称为“期望值准则”。
接下来我们就来仔细分析下“期望值”对我们究竟意味着什么。我们举一个简单的例子。
如果有彩票A和彩票B两种彩票,你很容易就能决定究竟该买哪一种。
- 彩票A:中奖概率为0.2,奖金2万元;
- 彩票B:中奖概率为0.2,奖金3万元。
由于中奖概率相同,那么购买中奖金额大的彩票B就是一个好的选择。
在下述情况下,你选择起来也不会有任何犹豫。
- 彩票A:中奖概率为0.3,奖金2万元;
- 彩票B:中奖概率为0.2,奖金2万元。
由于奖金相同,你当然是买中奖概率大的彩票A了。
真正会令人感到犹豫不决的是下述情况:
- 彩票A:中奖概率为0.2,奖金4万元;
- 彩票B:中奖概率为0.3,奖金2万元。
如果想要中更多奖金,你就应该选择彩票A;如果想要提高中奖概率,你就应该选择彩票B。在这种情况下,你会如何选择呢?
实际上,最自然的选择就是按照“比值”思考。与彩票A相比,彩票B的奖金只有一半。因此,如果想做到真正平衡,彩票B的中奖概率就应该是彩票A的2倍。但是,彩票B的中奖概率只有彩票A的1.5倍(0.3÷0.2=1.5),可以据此判断购买彩票A是合理的。
为了进一步强化判断标准的普适性,需要对比较的方法进行重新解释。
在对彩票奖金的比值和中奖概率的比值进行了比较,结果是4÷2>0.3÷0.2,从而推导出了应该购买哪种彩票的结果。根据不等式计算规则,原不等式可以转化为不等号两端最外侧的数值相乘之积>两端内侧数值相乘之积。因此,上述不等式相当于4×0.2>2×0.3。

这样一来,该不等式的左侧就变成了彩票A的奖金×彩票A的中奖概率,右侧变成了彩票B的奖金×彩票B的中奖概率。所以,“彩票奖金×中奖概率”就等于购买彩票有望获得的收益。我们将其称为“彩票奖金的期望值”。如果按照这种方式进行定义,彩票A的奖金期望值就是4万元×0.2=0.8万元,彩票B的奖金期望值就是2万元×0.3=0.6万元。前者的期望值较大。因此,可以判断购买彩票A是更为合理的选择。
假设一个人连续N次购买彩票A,并且这里的N是个非常大的数字。如果购买同一彩票的次数足够多,那么实际的中奖比例就会相对稳定,与概率基本相同,这种现象被称为“大数法则”。因此,可以得出实际中奖的次数=N×0.2。此时,赢得的奖金总额=4万元×N×0.2。如果求取奖金总额的平均值,所得的每次平均奖金金额=4万元×N×0.2÷N=4万元×0.2。这与彩票A的奖金期望值完全相同。也就是说,彩票的奖金期望值是多次购买同一彩票时的“单次平均中奖额”。
四、搏一搏,单车变摩托
在剩下的生意C和生意D中,我先介绍相对容易理解的选择生意D的决策方法。生意D所蕴含的思维方式与生意B截然相反,它将关注的重点全部聚焦在“可能实现的最大利润上”。在所有生意中,可实现的最大利润为500元,也就是选择生意D并且天气状况为阴时。
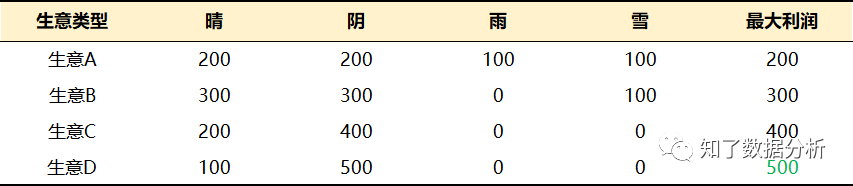
人们将这种“追求可能实现的最大利润值”的决策标准称为“最大最大准则”。其基本思路是优中选优,先找出各种情况下利润最多的情况,然后进行比较,从中选择利润最多的情况。
在这种决策准则指导下,人们会“想象最理想的情况,并据此选择决策方式”。可以说,这是一种看起来近乎盲目乐观、缺乏思考的行动准则。
这一准则与赌徒的心理有许多相似之处。比如,对于赌博游戏,如果根据期望值准则进行判断,无论哪种形式的赌博,都是“稳赔不赚”的选择。尽管如此,还是有许多人沉迷于赌博不能自拔。这究竟是为什么呢?
有一个用来描述热衷于博彩的人的心理——侥幸心理。侥幸心理主要用来表达人们冒险时希望获得意外收益的心情。高额的获奖奖励会激发人们的侥幸心理,刺激人们参与博彩。
这一准则“在做决策时仅考虑最为有利的情况”。也就是说,“最大最大准则”是人们在充满期待的心理状态下,坚持认为“虽然没有什么依据,但是肯定会发生对自己有利的事情”,并据此做出行为决策。虽然从理论上来看,几乎不会出现对所有人都有利的情况,但让所有人相信事情会对自己有利是完全可能的。人们并不会参考概率,也不会参考期望值。这是因为无论是概率还是期望值,都是多次性指标,而不是一次性指标。
我认为“侥幸心理”和“最大最大准则”与“社会结构”之间是不可分割的。如果单纯从数学合理性的观点出发进行判断,它们是完全不合理的事情,也是完全无法解释的。但是,在“社会结构”这一相对而言更为宏观的框架下,它们则具有必然性。
在现实社会中,大多数人都过着平凡的日子,挣着接近平均水平的工资,住着普通的住宅,过着柴米油盐酱醋茶的生活。这种生活状态决定着普通人未来的财富和生活水平。
但是,彩票中奖可以给普通人的生活带来根本性的转机,彻底改变普通人对于未来生活轨迹的预期。普通人只要付出几块钱的代价,就可能帮助自己实现逆袭,赢得一个崭新的未来。这种颠覆性变化与概率和期望值根本不可同日而语。在这种情况下,人们脑海中所想的是自己作为“单纯个体存在”的“只有一次的人生”。可以说,这是一种与感觉偏差或概率偏差完全不同的人生观和生死观层面的概念。
然而,我们换一个角度来看,人生只有一次,我们不能片面地认为带有冒险赌博色彩的决策就一定是不合理的。人生无法重来,不能在重复成百上千次的基础上进行数据统计分析。因此,面对只有一次的人生,有些人去做一些高风险的尝试也是可以理解的。
大家的梦想五彩斑斓、各不相同,有的人希望成为音乐家,有的人希望成为游戏开发设计师,有的人希望成为动漫画家,有的人希望成为演员,有的人希望成为总统……与其在平平淡淡中碌碌无为地度过一生,还不如选择轰轰烈烈地赌上一场,追求一个充满刺激和挑战的未来,尽管这样做很可能会变得一事无成。这就是“最大最大准则”的思维逻辑。
只不过在做出这样的决策时有一点需要特别说明,当事人要非常清楚自己正在运用“最大最大准则”做出选择。此外,当事人还要明确自己眼前有哪些可以选择的机会,并对运用期望值进行对比分析后做出取舍的选项进行重新审视,最后,对因此会带来多少利益损失进行认真的评估,再做出最终的决定。正所谓“我的人生我做主”,在完成这一系列过程后,不管做出怎样的决定,都是每个人的自由。
由此可见,“最大最大准则”也具有一定的合理性。
五、捡了芝麻,丢了西瓜
选择生意C的人,其逻辑是比较复杂的,多数人不太容易理解。实际上,在进行调查的过程中,有部分人会选择这个选项。
人们之所以会选择这个生意,是由于“后悔”这种思维方式发挥了作用。如果先从结果出发,向大家说明这种选择标准的实质,那么可以说,选择生意C是一种“可以将今后后悔的概率降到最低”的决策方式。
如果说得再详细一点,在选择其他生意(A、B、D)的情况下,大家关注的往往是“吃亏最大”情况下的损失。
当你选择生意A时,如果天气为晴的话,你可能会感到后悔,觉得“早知道当初选择生意B就好了”。因为如果选择生意B,在晴天的情况下,可以赚300元,现在自己选择了生意A,结果只能赚200元,丧失了多获得利润的机会。
这种情况下的损失是100元。在经济学专业术语中,这种损失叫作“机会损失”。机会损失会将你做出其他选择时可能产生的利润差额计算为损失,这意味着现行选择所获收益小于已放弃选择可能获得的潜在收益。当天气为阴时,如果选择生意D,可以获得500元的收益,机会损失就是300元(500-200)。
同理,当天气为雨时,机会损失为-100元(0-100),相当于盈利了100元,可以忽略不计。当天气状况为雪时,机会损失为0元。总结一下,选择生意A时的最大后悔值(最大机会损失)为300元。
在选择生意B的情况下,与选择生意D且天气为阴的情况相比,会产生最大后悔值,为200元(500-300)。
在选择生意D的情况下,与选择生意B且天气为晴的情况相比,会产生最大后悔值,为200元(300-100)。
在选择生意C的情况下,无论天气状况如何,后悔值都是100元(300-200、500-400、100-0、100-0),因此最大机会损失就是100元。与选择其他三种生意相比,其最大机会损失是最小的。也就是说,选择生意C的后悔值是最小的。
由此可见,将后悔值降到最低,以防出现“后悔药没处买”的情况,与“将最大机会损失控制在最小范围”的想法是完全一致的。因此,人们将这种决策标准称为“最小机会损失准则”。这一理论最早是由著名学者沙万奇提出的,因此学术界往往将其称为“沙万奇准则”。
机会损失是经济学领域经常用来换个角度思考问题的概念,是指“将用于既有决策的时间和精力投入到采用其他决策的行动中时可能获得的收益”。我们应该将其视为决策时付出的成本(cost)。
人们经常会为自己的选择感到后悔。这是因为大家总会预测“自己曾经擦肩而过的选择到底会带来怎样的结局”,并不自觉地产生“如果当初那样做了,就不会落到现在这种局面”的想法。这种思维方式在生活中也非常常见。
例如,当买了某件商品后,第二天亲眼看见同一家店在售的相同商品突然降价时,你肯定会后悔“早知道等一天再买就好了”;当开车出门遇到堵车时,你肯定会后悔“早知道坐地铁好了”;当卖掉的股票突然大幅上涨时,你肯定会后悔“如果当时不卖就好了,那现在就可以赚大钱了”。
虽然人们总是说“既往不恋”,但是通过后悔和反思,还是能够发现自己行为当中草率、冒失、缺乏考虑的问题。
这一准则就是以“后悔”的心理状态为出发点和着眼点的,它提出的建议非常简单,概括起来就是“针对未来可能发生的各种事态,都要提前考虑,事先评估自己选择某种行为后,将来是否会为此而感到后悔,具体又会后悔到什么程度”。也就是说,“要后悔在前头,提前感受后悔带来的影响”。
人们感到最懊悔的事情莫过于“突然发生了自己完全没有预想过的状况,并且为此蒙受了出乎意料的损失”。如果能够正确运用“最小机会损失准则”,至少可以避免遭遇“意料之外”的状况。这是因为在充分考虑所有可能发生的状况和由此带来的损失的基础上,人们可以做出更为合理的决策,从而降低将来后悔的风险。就算将来真的发生什么状况,人们也可以冷静对待。从这个意义上来看,运用“最小机会损失准则”是非常有利的。
然而在现实生活中,大部分人根本注意不到机会损失的存在。不信,我们来看几个小例子,可能你或多或少都经历过。
比如,我们有没有问过自己:“你知道为了上大学,自己要付出多少成本吗?”大多数人认为我就只需要付出一些学费,也没有什么其他的成本啊。这可能是一种普遍的认识。由此可见,要想帮助大家意识到“机会损失”的存在是一件多么困难的事情。
实际上,大家忽视的是一个问题:如果一个人在高中毕业后,没有上大学,而是进入社会就业,那么在四年间究竟可以赚多少钱呢?假设每年能赚10万元,上大学四年的成本就是学费加上40万元。所以,至少在这四年间,我们为读大学要付出如此高昂的代价。
再比如,有些人经常炫耀在自己家的门头开店营业,没有房租费用,因此非常赚钱,这也是忽视机会损失的典型代表。从经济学的角度来看,忽视机会损失是一个严重的认知误区。
某人打算将自家的一楼改造成商铺对外出租。如果直接将商铺租给其他人而不是自己开店,这个人每个月可以收入20万元的房租;而如果将商铺用于自己开店而不是租给别人,我们就应该将20万元计入经营的成本之中。之所以这样计算,是因为这个人直接放弃了出租房屋可以带来的20万元的预期收入。这也是一种机会损失。
我们可以进一步思考,当利润(营业收入扣除营业成本后的金额)低于多少时,应该停止经营。对于那些未将房租这一机会损失纳入成本考虑的人而言,只要利润为正值,就会一直经营下去。
但是,这种观点实际上是错误的。当开店的月利润只有15万元时,这个金额是低于20万元的房租的,那么,这个人就应该立即停业,将一楼的商铺以20万元的价格租给其他人。如果不这样做,就相当于为了15万元的利润而眼睁睁看着20万元的收益白白溜走,可谓是“捡了芝麻,丢了西瓜”。我们这里还没有考虑因自己经营店铺而损失的个人外出工作的潜在收益。
理解了通过概率思维进行决策的底层逻辑之后,我们就能明白“选择大于努力”这句话,从概率的角度看是存在科学依据的。同样的机会,人生算法不同,结果也就不同。
以上就是本期内容分享。下一篇文章,将给大家介绍两种非常实用的决策方法,让大家在面对人生各种各样的问题时能够更灵活使用概率思维指导决策。
微信公众号:知了数据分析
本文作者 @知了数据分析 。
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
