「管理数学基础」3.1 凸分析：凸集与凸集分离定理、Farkas引理

凸集与凸集分离定理、Farkas引理

文章目录

• 凸集与凸集分离定理、Farkas引理
• • 凸集
  • • 定义：凸集
    • 凸集性质（逐个证明）
  • 超平面
  • • 定义：超平面
    • 证明：超平面是凸集
    • 定义：支撑超平面
    • 定义：多面体
    • 定义：凸锥
  • 凸集分离定理
  • • 定义：分离
    • 定义：凸集分离定理
  • Farkas引理
  • • 定义：Farkas引理
    • 证明：Farkas引理

凸集

定义：凸集

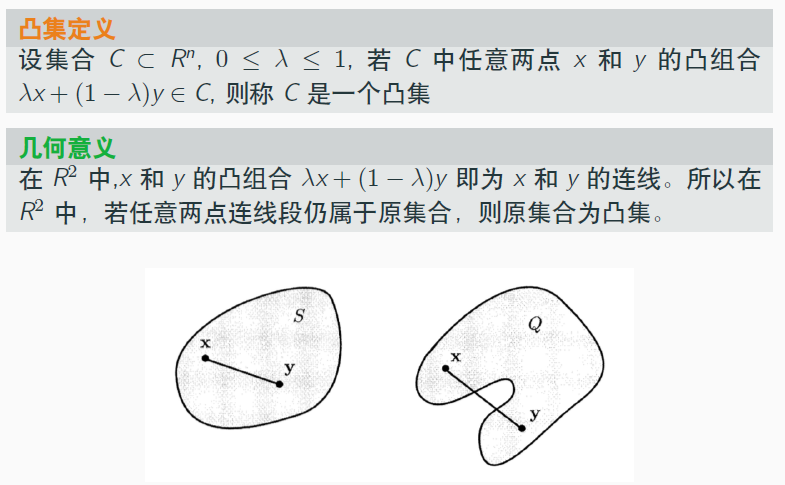
注意凸集的定义，任取两点满足某个条件为凸集：

• 证明是凸集的目标有了
• 凸集的性质也有了，可以利用

凸集性质（逐个证明）

(1)

分析：

• 任取 x A , y A ∈ λ C x_A,y_A \in \lambda C xA​,yA​∈λC，因为是要证明$\lambda C$是凸集
• 也就是要对于所有的 x A , y A ∈ λ C , β ∈ [ 0 , 1 ] x_A,y_A \in \lambda C,\beta \in [0,1] xA​,yA​∈λC,β∈[0,1]，都有 β x A + ( 1 − β ) y A ∈ λ C \beta x_A + (1-\beta) y_A \in \lambda C βxA​+(1−β)yA​∈λC
• 能利用的性质只有$C$是凸集以及$C$与$\lambda C$两个集合的关系（从微观上，一定存在$C$中元素乘上实数$\lambda$在$\lambda C$中），应该在二者间建立联系

(2)

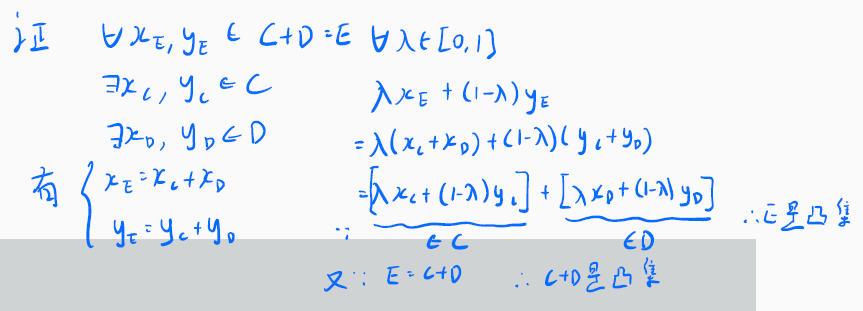
分析：

• 与上一题思路相同

(3)

有限个凸集的交集为凸集。

由以上凸集性质，我们做下面两点例题。

分析：

• 分别在集合间取元素，根据集合性质建立元素间关系
• 然后带回去，这样从原理出发计算不会出错

超平面

定义：超平面

分析：

• a ′ x = b a' x = b a′x=b在 R 2 R^2 R2是直线，在 R 3 R^3 R3是平面，在 R k , k > 3 R^k,k>3 Rk,k>3当然就是超平面了
• 注意$a$实际上超平面的法向量，与超平面垂直； b ∈ R 1 b\in R^1 b∈R1决定了超平面的位置
• 闭半空间一共有两个（一侧的点与法向量构成锐角，一侧是锐角）

证明：超平面是凸集

很简单，对于闭半空间是凸集同理，将$=$换成$\le$或$\ge$即可。

定义：支撑超平面

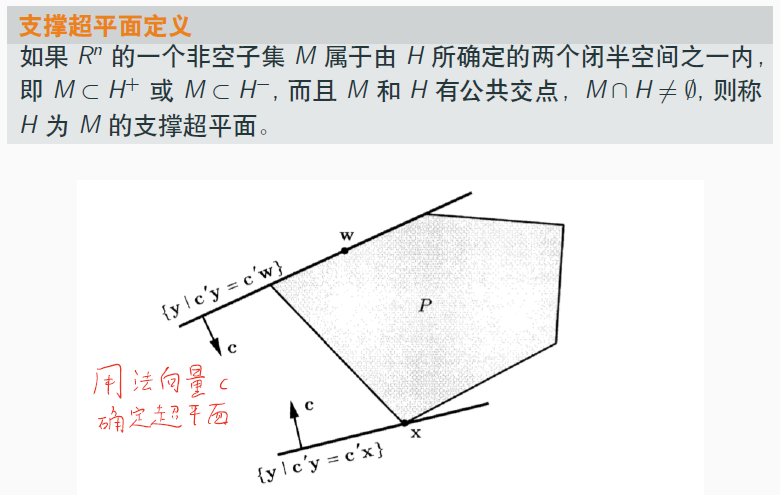
分析：

• “支撑”即超平面对这个空间的生成起了作用，“触碰”到了这个空间

定义：多面体

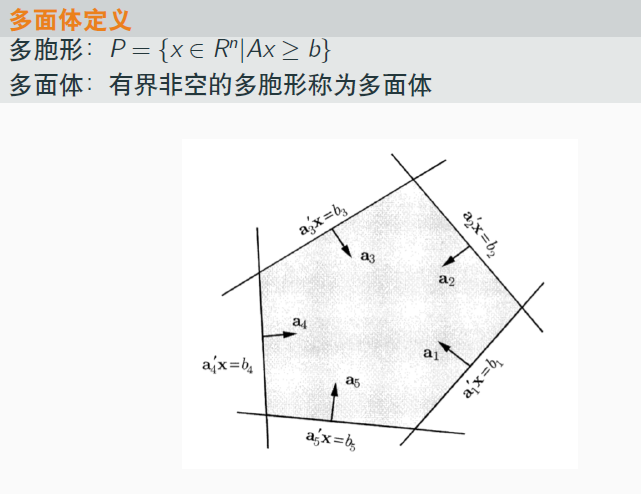
多面体：

• 是多胞形（上图的多胞形定义，我觉得不对）
• 有界非空

定义：凸锥

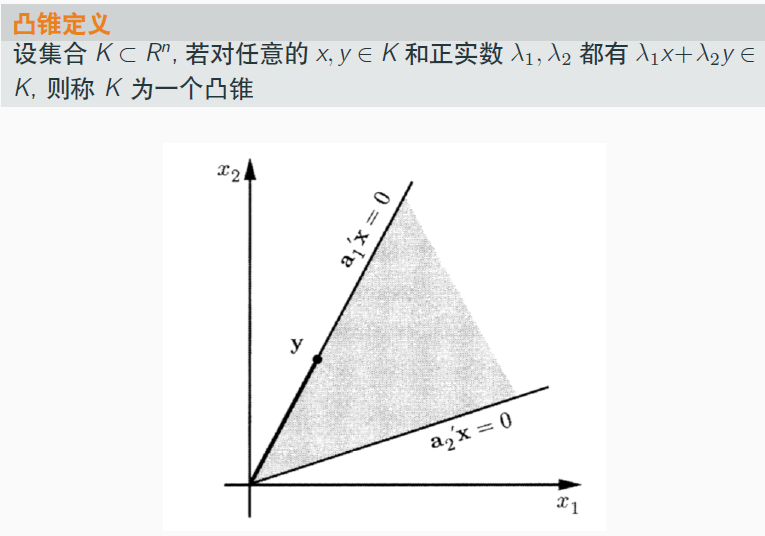
分析：

• 经过原点 0 ⃗ \vec{0} 0 ，因此超平面中$b=0$
• λ 1 x \lambda_1 x λ1​x 与 λ 2 y \lambda_2 y λ2​y 相加，实际上表示了两个超平面的中和，即相互趋近

凸集分离定理

定义：分离

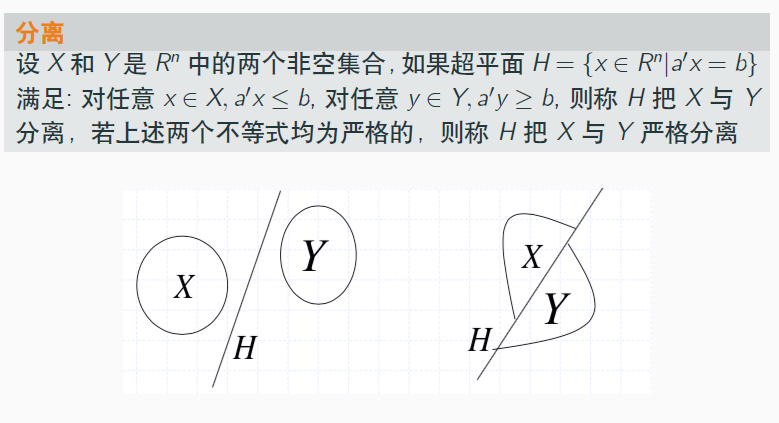
分析：

• 两个非空集合，可以被几何的概念（超平面）分开，不重叠（但是可以重叠在超平面上）
• 如果没有$\le$与$\ge$即等号关系，则是严格分离

定义：凸集分离定理

如上是凸集分离定理（如果两个集合是不相交的凸集，那么可以被一个超平面分开）。

证明过程很长，证明并应用了：Weierstrass定理、点集严格分离定理、支撑超平面定理。

Farkas引理

定义：Farkas引理

用于后面的凸规划，这里注意一点：

• (1)有解了，(2)必无解

证明：Farkas引理

首先，假设(1)有解，证明(2)无解即可；接着证明(1)无解情况下，(2)必有解，大概思路是：

• $\forall y\in S$，由(1)无解可得$b\notin S$，由此，利用点集分离定理，得到 p ′ b < p ′ y p' b < p' y p′b<p′y
• 进一步，由$0\in S$，则有 p ′ b < 0 p'b < 0 p′b<0，现在(2)的第二个式子已经证明完毕了，接下来是第一个式子 p ′ A ≥ 0 p'A \ge 0 p′A≥0的证明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！