NYOJ 78 圈水池
圈水池
时间限制:3000 ms | 内存限制:65535 KB
描述
- 输入
- 第一行输入的是N,代表用N组测试数据(1<=N<=10)
第二行输入的是m,代表本组测试数据共有m个供水装置(3<=m<=100)
接下来m行代表的是各个供水装置的横纵坐标 输出 - 输出各个篱笆经过各个供水装置的坐标点,并且按照x轴坐标值从小到大输出,如果x轴坐标值相同,再安照y轴坐标值从小到大输出 样例输入
-
1 4 0 0 1 1 2 3 3 0
样例输出 -
0 0 2 3 3 0
分析:把供水装置圈起来,只需要把最外面的圈起来即可,这就用到了凸包。
解决凸包有很多算法 ,我这里用到 Graham扫描法 时间复杂度:O(n㏒n)
步骤:
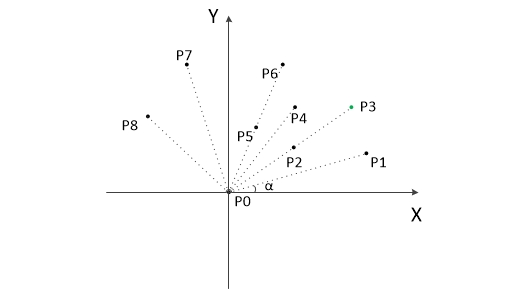
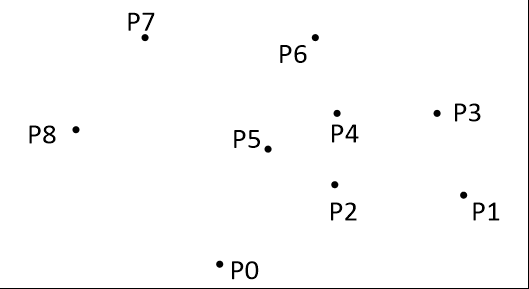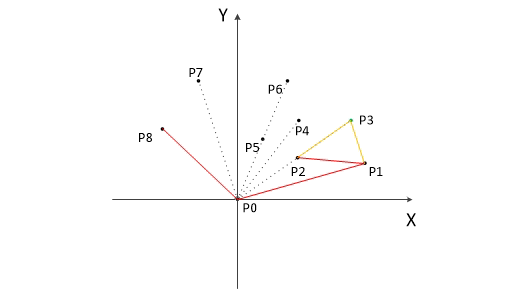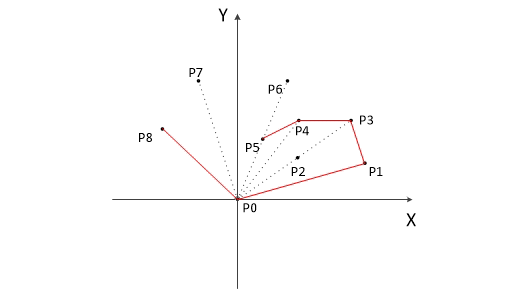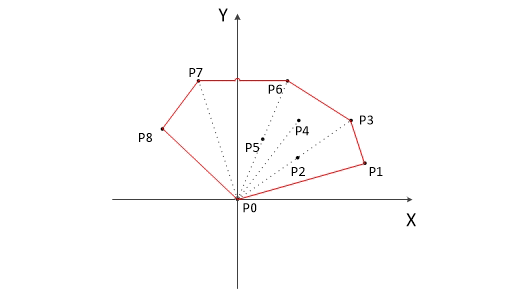
把所有点放在二维坐标系中,则纵坐标最小的点一定是凸包上的点,如图中的P0。
把所有点的坐标平移一下,使 P0 作为原点,如上图。
计算各个点相对于 P0 的幅角 α ,按从小到大的顺序对各个点排序。当 α 相同时,距离 P0 比较近的排在前面。例如上图得到的结果为 P1,P2,P3, P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一个点 P8 一定是凸包上的点。
(以上是准备步骤,以下开始求凸包)
以上,我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的那个点拿出来做当前点,即 P2 。接下来开始找第三个点:
连接P0和栈顶的那个点,得到直线 L 。看当前点是在直线 L 的右边还是左边。如果在直线的右边就执行步骤5;如果在直线上,或者在直线的左边就执行步骤6。
如果在右边,则栈顶的那个元素不是凸包上的点,把栈顶元素出栈。执行步骤4。
当前点是凸包上的点,把它压入栈,执行步骤7。
检查当前的点 P2 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 P2 后面那个点做当前点,返回步骤4。
最后,栈中的元素就是凸包上的点了。
以下为用Graham扫描法动态求解的过程:
#include
#include
#include
using namespace std;
int n,top;
struct point
{int x,y;
} p[1005],s[1005],t;
double cross(point t1,point t2,point t3,point t4) //求向量t1t2和向量t3t4的叉积
{return (t2.x-t1.x)*(t4.y-t3.y)-(t2.y-t1.y)*(t4.x-t3.x);
}
double dis(point t1,point t2) //求距离
{double z=(t2.x-t1.x)*(t2.x-t1.x)+(t2.y-t1.y)*(t2.y-t1.y);return sqrt(z);
}
bool cmp(point t1,point t2)
{double z=cross(p[0],t1,p[0],t2);return z?z>0:dis(p[0],t1)p[i].y||(t.y==p[i].y&&t.x>p[i].x)){j=i;t=p[i];}}t=p[0];p[0]=p[j];p[j]=t;
}
void scanner()
{int i;findpoint();sort(p+1,p+n,cmp);for(i = 0; i < n; i++)s[0]=p[0]; //排好序后最开始的点一定是凸包上的点s[1]=p[1];top=1;for(i=2; i 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!