数据可视化当中的图表组合:比例面积图
很多时候由于国内数据可视化行业相较于西方国家起步比较晚,所以很多时候我们在进行数据可视化的时候只会选用单个图表来进行数据分析的呈现,有的时候其实多种图表直接是可以相互组合的。
就比如以比例面积图来说,它的结构很简单(形状的面积与其表示的数据值成正比),这使比例面积图易于附加到其他图,这样分析出来的信息能够给我们传递更多的信息,那么我针对比例面积图收集了以下33种不同的组合形式分享给大家:
01 + 100%堆积条形图
通过与100%堆积的条形图结合,形状区域被分为多个部分以传达零件与整体的关系。
在下面的示例中,每个正方形代表一个国家的GDP,该债务的GDP数量用红色表示。通过将每个正方形分为两个部分,你可以查看到哪些国家负债最多。
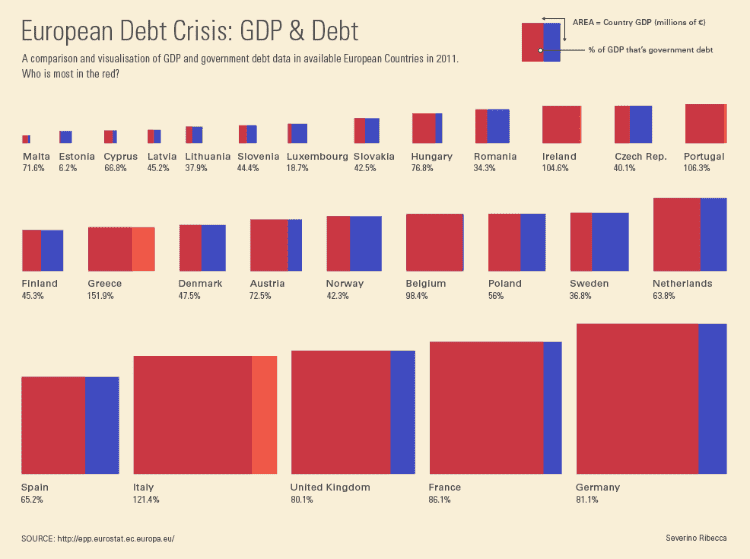
资料来源:欧洲债务危机:GDP与债务,Severino Ribecca
我发现这种风格的比例面积图从一个更早的迭代第九次人口普查(1870)的统计地图集由弗朗西斯·沃尔克。在这里,美国各州的形状区域是根据该人口中每个教会支配的比例来划分的:

资料来源: 自由基制图
02 +条形图
通过与条形图组合,可以通过在每个条形图的底部放置形状区域来向图表提供其他变量。
以下是标题为“皮埃蒙特的分析旅游地图”的信息图的一部分,该图 已使用比例区域图和条形图分割了意大利皮埃蒙特地区的旅游流量:
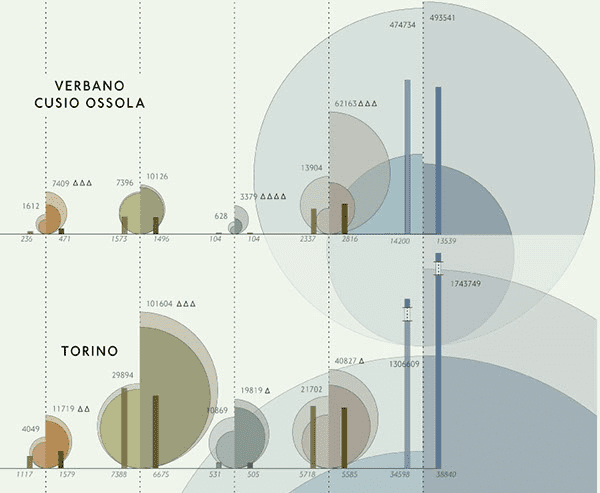
资料来源:Behance皮埃蒙特分析旅游地图
03 +表格/矩阵
你可以将比例面积图与表格结合起来以形成用作相关矩阵的图表。这是通过为行和列中的一个类别分配尺寸,并在两个类别相交的表单元格中绘制形状区域来实现的。
在下面的示例中,圆圈的大小与每个团队在给定任务上花费的时间有关:
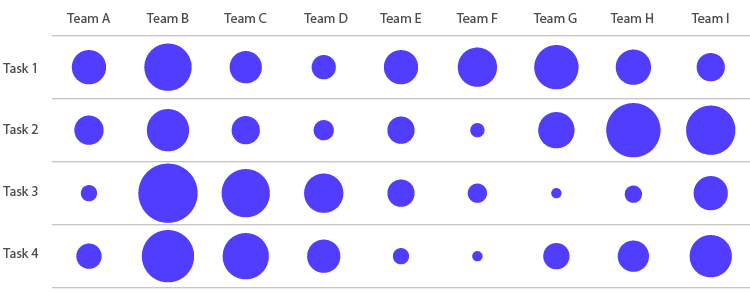
该图表对于发现两个类别或变量之间的相关性以及查找数据中的模式很有用。
04 +热点图(矩阵)
我们可以通过更改形状区域相对于该附加变量的颜色,来向先前的图表添加一个附加变量(例如在Heatmap中)。
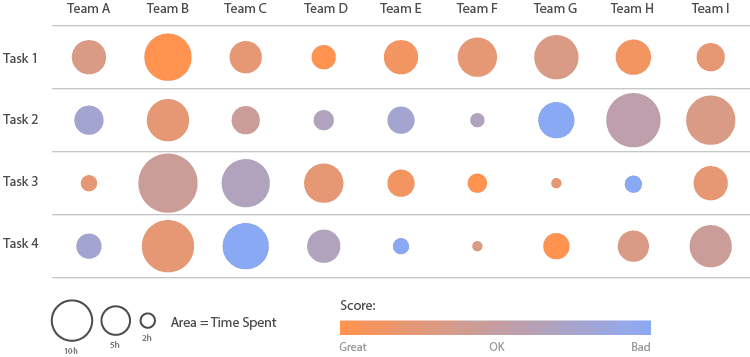
05 +日历
与日历结合使用的方式与与表格结合使用的方式相同。形状区域放置在每个日期单元格内,以可视化特定日期发生的值。在这里,可以查看值在特定月份的变化情况。可以通过按比例改变每个形状区域的阴影或颜色来显示其他变量。
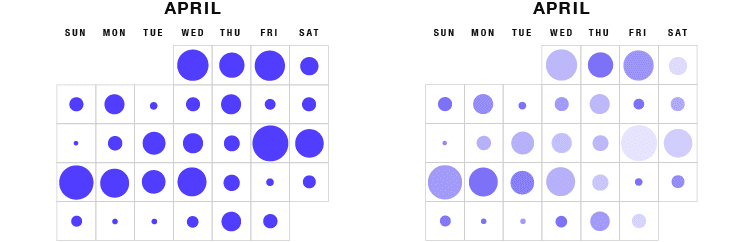
06 +插图
比例区域图可以覆盖在插图或照片上,以提供有关主题的更多信息,从而生成可以显示定量值的插图。在下面的《华尔街日报》的以下示例中,在NFL球员身体的各个部分上显示了圆圈区域,以说明受伤最多的地方。
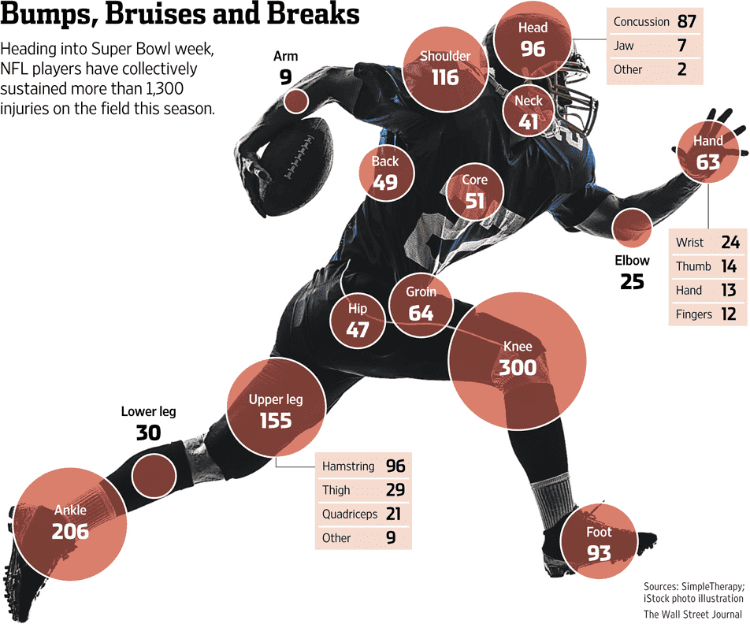
来源:《华尔街日报》
07 +地图
将比例区域图与地图组合会生成气泡图 (如果使用圆形)。在此,圆显示在指定的地理区域内,圆的面积与数据集中的相应值成正比。当然,如果需要,可以用正方形代替圆形,但是圆形看起来会更好。
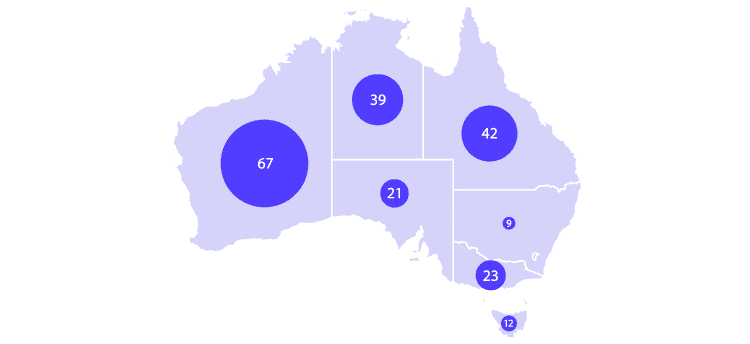
08 +连接图
也可以通过在每对连接点上绘制形状区域来将比例区域图应用于连接图。在此,可以将定量值添加到地图上的每个点以提供其他数据。
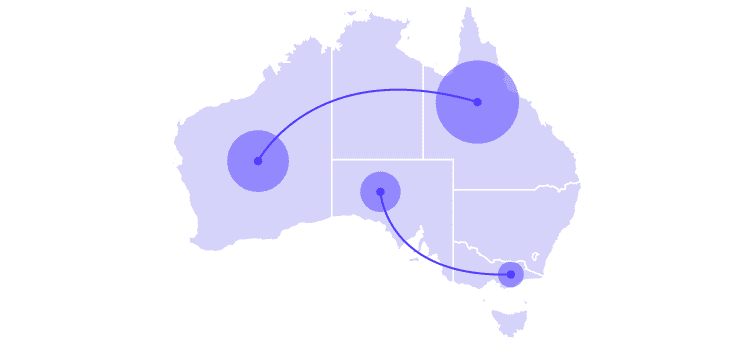
09 +瓷砖网格图
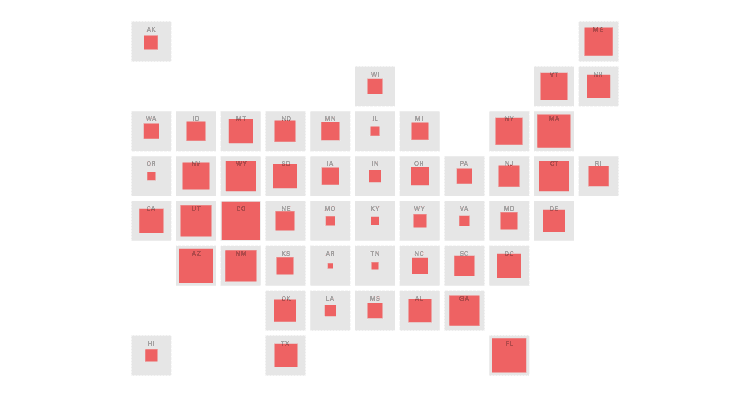
通过与“平铺网格图”结合使用,可以在地理块上显示形状区域。缺少变化的区域大小使得在每个区域进行比较变得容易。以下是一些使用比例面积图的不同变体的示例。
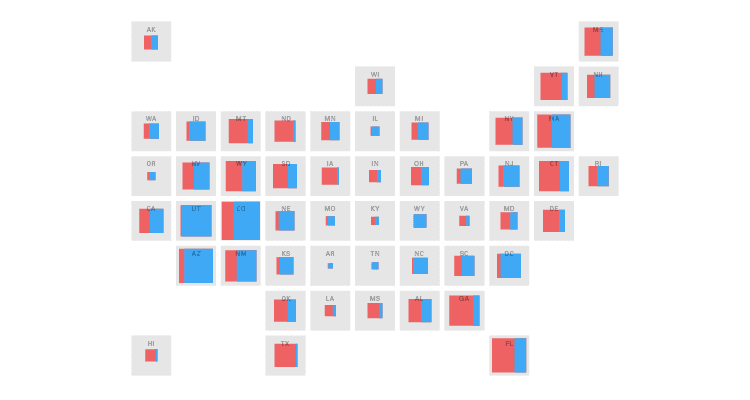
10+制图
可以通过将地图上的地理区域转换为形状并根据数据更改其大小来将制图图与比例区域图结合起来。然后需要以与原始拓扑大致相似的方式组织和定位形状区域。如果使用圆圈,则这种类型的图表称为Dorling Map。
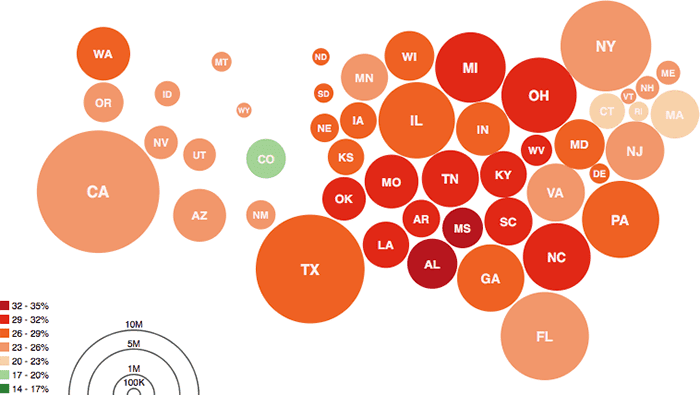
资料来源: Protovis
如果使用正方形,则这种图表称为Demers Cartogram。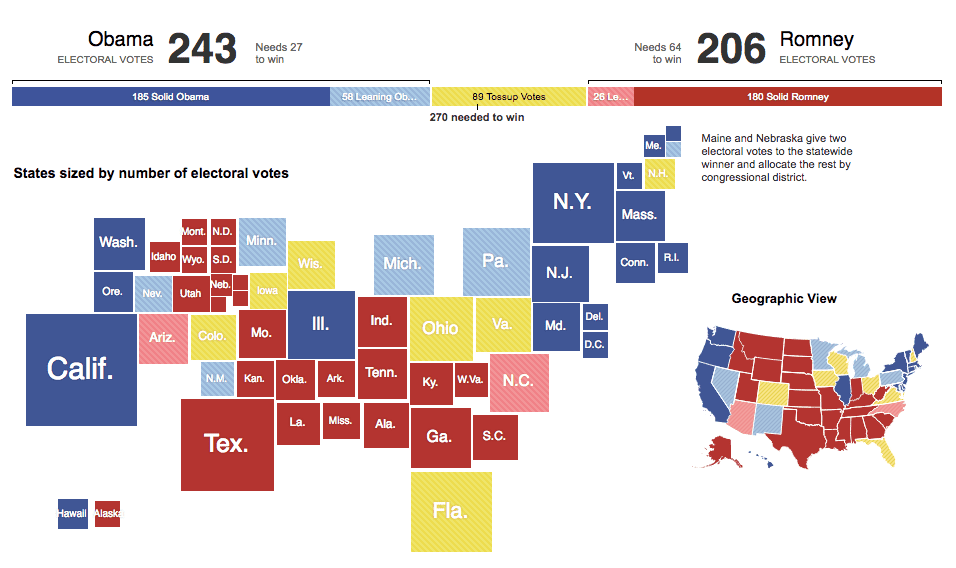
来源:《选举地图:通往胜利的道路》,《纽约时报》
11 +散点图
当然,将比例面积图与散点图结合起来会产生众所周知的 气泡图。在此,将点转换为面积与第三变量成比例的大小不同的圆。
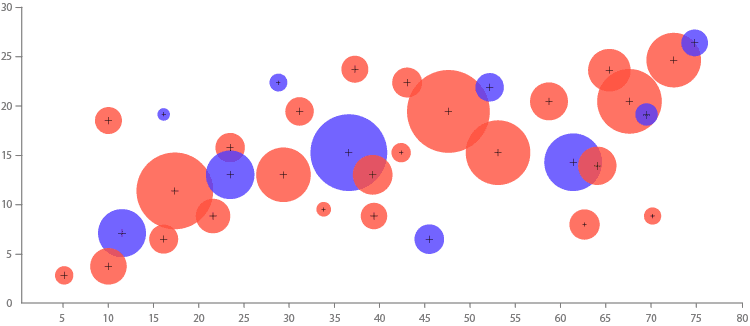
12 +连接散点图
当与连接散点图结合使用时,可以将形状区域应用于每个点以可视化其他变量。
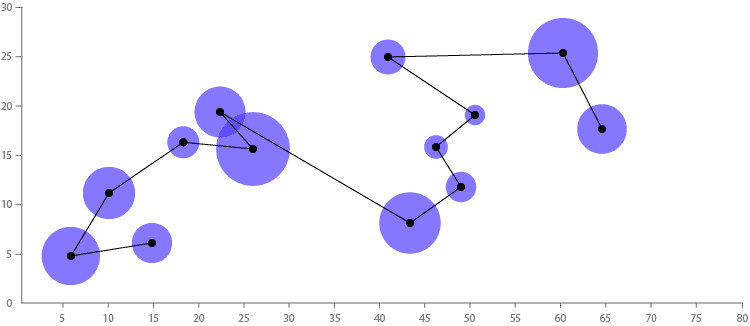
13+线图
与折线图组合时,可以应用相同的方法,并为时间序列数据提供其他变量。
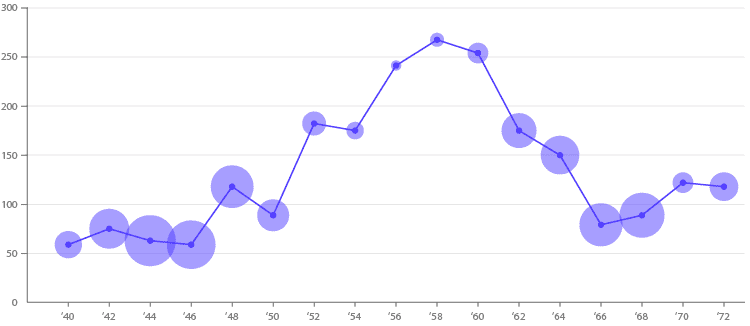
14+坡度图
与坡度图结合使用时,可以看到其他变量在两个时间点之间如何变化。
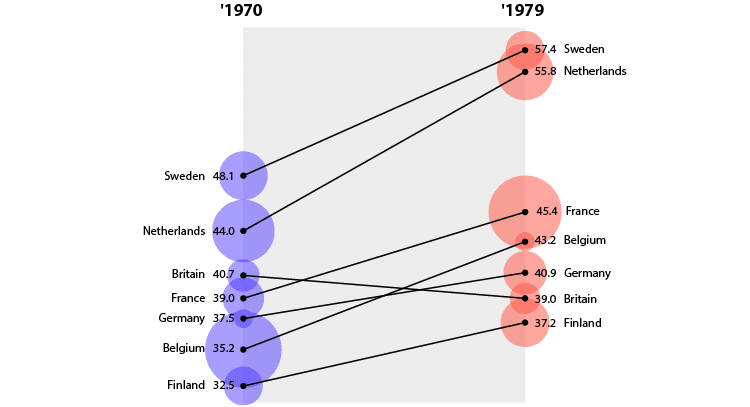
15 +雷达图
与绘制点的所有图表一样,将形状区域附加到这些点以显示其他变量也很容易。通过与“雷达图”结合使用,那你将获得如下图所示的图表。
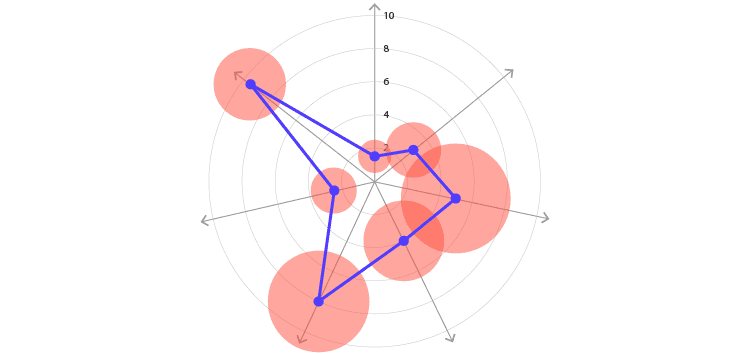
16 +跨度图
要为范围数据提供其他变量,可以将比例面积图和跨度图组合在一起。在这里,形状区域被附加到钢筋的中间,而不是被添加到最大值和最小值的每一端。
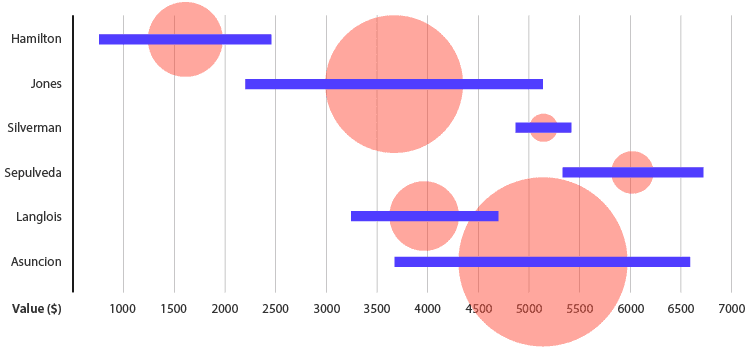
17 +连接点图/哑铃图
如果你想让图表更多地关注范围数据中的最小值和最大值,那么与哑铃图结合将是一个更好的解决方案。在下面的示例中,有两个变量连接在一起:男性BMI(蓝色)和女性BMI(粉红色)。这显示了不同国家的两个性别之间存在多少差异(BMI)。可以将附加变量与这两个变量中的每一个一起添加,并通过在每个点上显示的形状区域显示。

18 + 双向哑铃图
它的功能有点类似于散点图,其中每个轴都是变量,并且绘制了点。但是,使用此图表,可以绘制类别的前/后值,例如在坡度图中,但也可以在每个点上提供附加值,并通过形状区域大小可视化。下面我演示了这一点,其中蓝色是一种类别,红色是另一种类别:
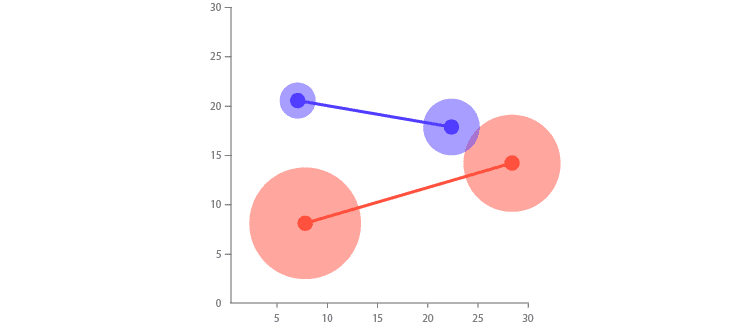
19 +点图
与点图组合非常简单,只需在每个点上添加一个形状区域即可可视化其他变量。
20+双点图
点图还可以选择显示数据集中更改前后的变化,或者通过在同一行上包含两个具有不同颜色的点来将两个变量相互比较。当然,可以通过改变形状区域的大小来添加其他变量。
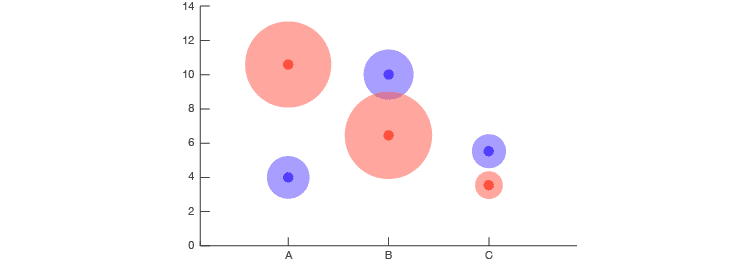
21+棒棒糖图表
与棒棒糖图结合使用的方式与与点图(将点放置在形状区域中)的方式完全相同。
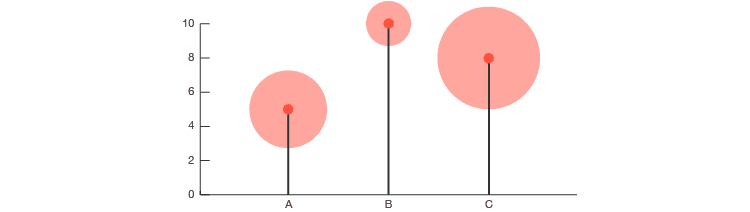
22 +三元图
与三元图结合使用,可以一次可视化四个不同的变量(第四个以形状区域大小表示)。
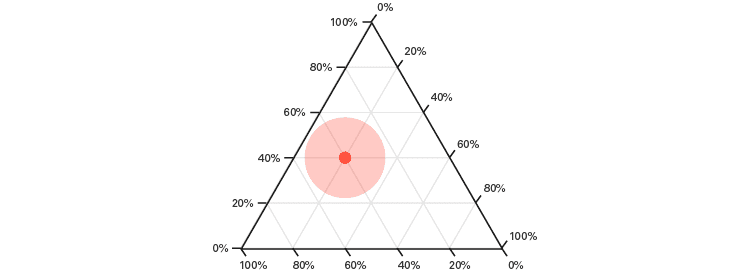
下面的交互式示例甚至使用了可以称为“三元气泡图”的内容。尽管此示例仅显示四个变量(每个政治候选人3个,形状区域的大小由每个地区的投票数决定),但可以将第五个变量分配给颜色阴影(在下面的示例中,颜色仍然是由3个政治候选人变量决定)。阅读更多在这里这个图的结构。
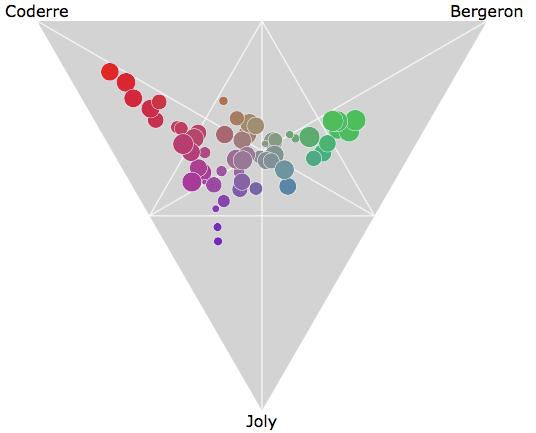
来源:2013年蒙特利尔市长选举
23 +项目符号图
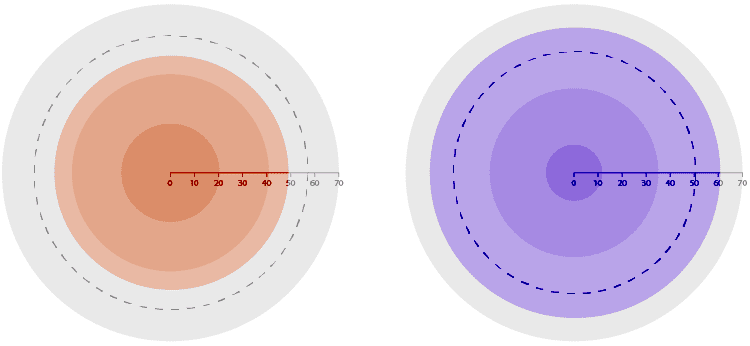
可以制作子弹图的比例区域图版本。在下面,我使用圆的面积来创建“圆形项目符号图”,但是也可以使用正方形来构造此图表。
在下面的示例中,定性分数范围 由三个灰色圆圈区域表示,特征量度 (分数)由彩色圆圈区域表示。提供了一个刻度以帮助读取值,并且 用虚线表示比较度量(目标)。
24 +饼图
改变饼图的面积大小是一种可视化比例的方法。但是,就最佳实践而言,我强烈建议不要使用此方法,因为这样做时,人们无法准确地阅读和比较每个楔子。同样,楔形的大小变化也可以用来误导人们。
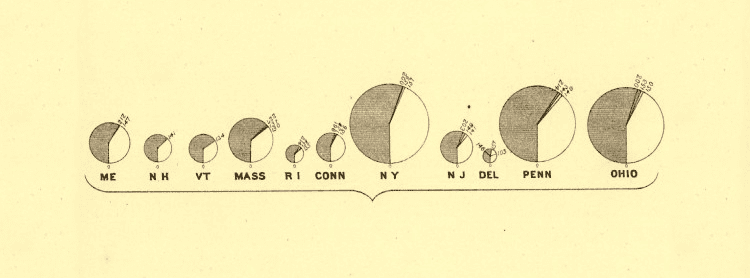
资料来源:显示白痴总数的图表,《第九次人口普查统计图集》(1870年),《径向图》
25 +华夫饼图
可视化百分比和比例的另一种方法是将比例面积图和华夫饼图组合在一起。
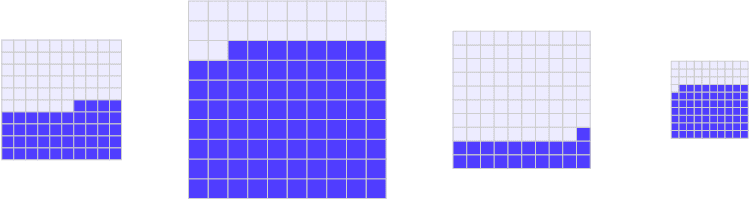
26 +树状图或Marimekko
通过更改每个块的大小,可以将其与迷你树形图或Marimekko图表结合使用。当然,在所有块之间,类别和变量必须一致并且使用相同的数据集。

尽管并不完全相同,但《第九次人口普查统计图集》(1870)中的 这两个旧示例 提供了两个很好的示例:

资料来源:第九次人口普查统计图集(1870年),《径向图》
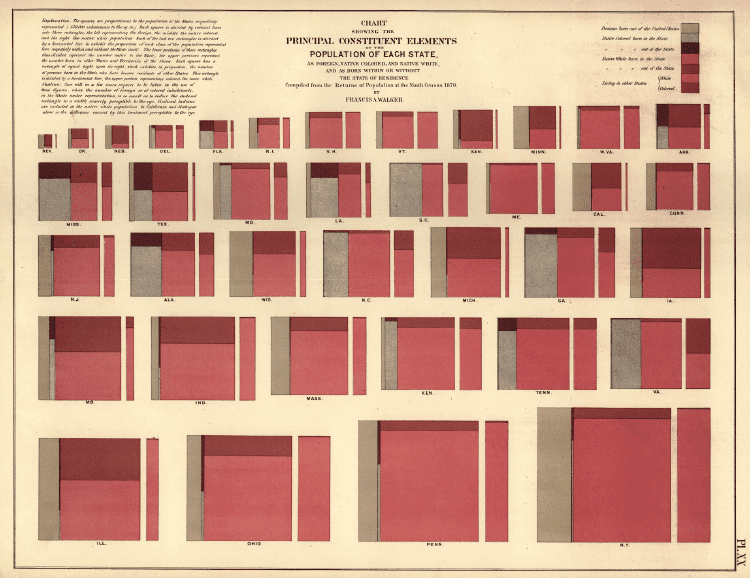
资料来源:第九次人口普查统计图集(1870年),《径向图》
27 +时间轴
与时间轴结合可以通过两种方式完成。首先(在左侧),将形状区域直接放置在时间线上,形状中心位于与数据关联的日期。其次(在右侧),你可以将形状区域放置在远离时间轴的位置,但是可以使用标注线更清楚地显示形状区域对应的日期。第二个选项还允许通过可能垂直变化的位置来应对由许多形状重叠引起的混乱。
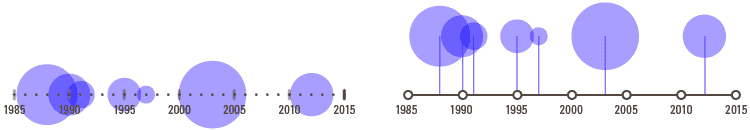
你可以通过为每个类别使用时间轴并将它们排列成一行来比较多个类别中的数据。以下是《金融时报》的一个很好的例子:
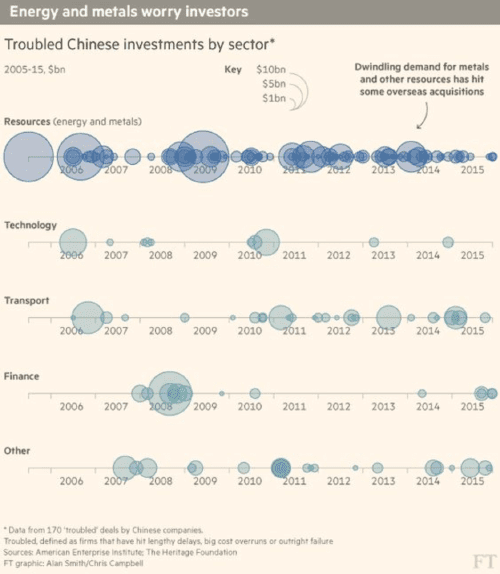
资料来源:《金融时报》
28 +网络
通过更改网络节点的面积大小并使它们与定量值成比例,从而将比例区域图与网络图结合起来。一个很好的例子是信息图表 20世纪,“信息是美丽的死亡”中,人类的不同死亡原因被分类地联系在一起,每个类别或子类别下造成的死亡数量以每个圆圈的面积表示。
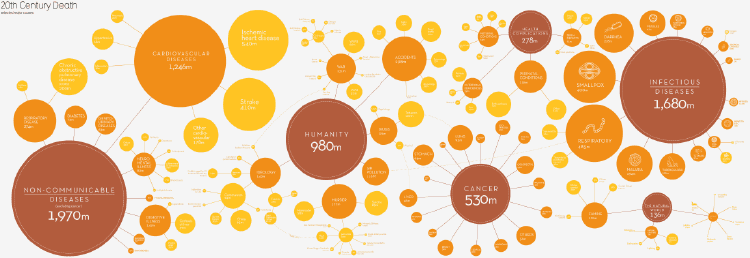
资料来源:20世纪的死亡,信息是美丽的
另一个很好的例子来自《纽约时报》,他绘制了许多不同的人类疾病或病症的图谱,并根据与该疾病或病症相关的基因数量成比例地改变了结节的大小。
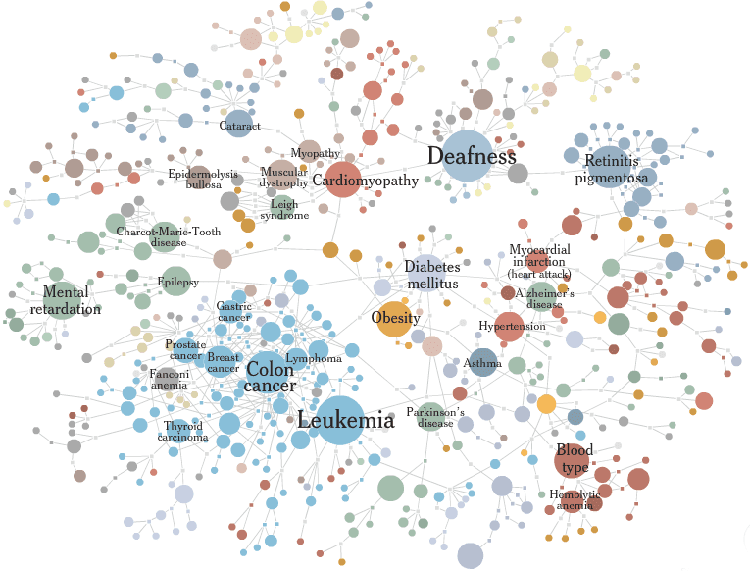
资料来源:《纽约时报》绘制人类的“恶魔”
29 +树形图
通过与树形图结合,可以将比例区域图与层次结构数据一起使用。在此,可以在树形图的每个节点/成员上显示其他定量值,以提供有关它们的更多信息。
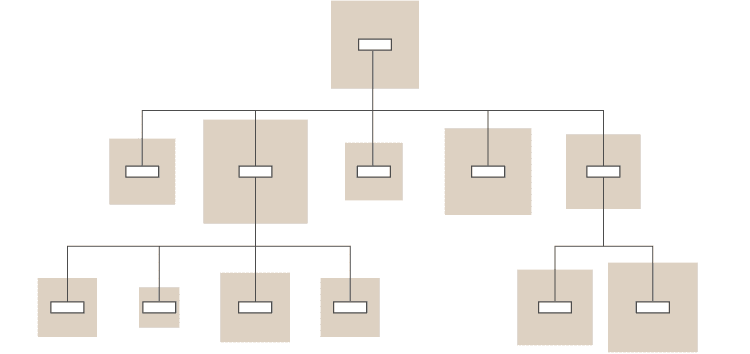
30 +圆形树形图
除了线性格式,你还可以将组合应用于树形图的圆形布局。下图有点神秘(我只能发现它是由“ Sophie”设计的,并且是为一家名为“ Help”的公司完成的),但是它提供了这种组合的一个很好的例子。
尽管尚不清楚面积的大小或圆圈的颜色代表什么,但此图显示了大量的非处方药,这些药物可用于简单的头痛。从“我头疼”开始,此图指导你完成选择特定品牌时可能要经历的各种决策过程。
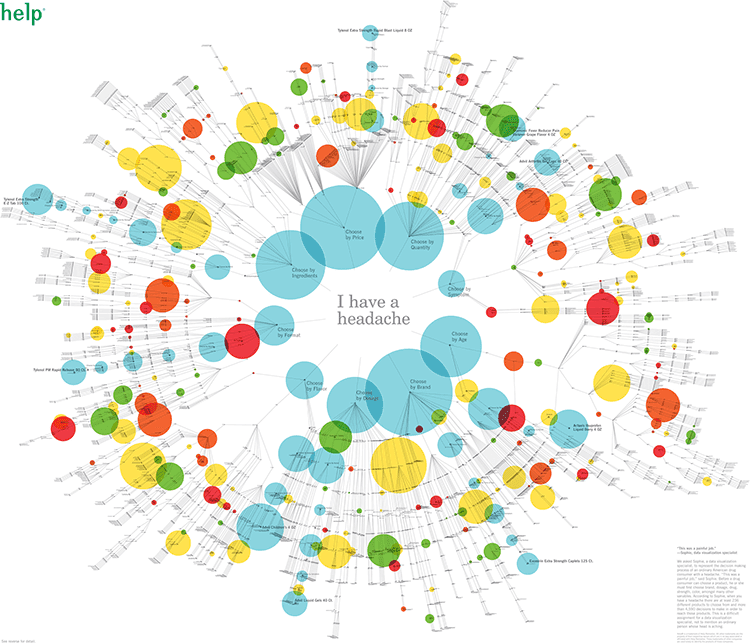
来源:每日信息图:您在FastCompany药房面临的疯狂选择
31 +弧形图
与“弧形图”组合时,将形状区域放置在节点上以提供与其相关的其他变量。Martin Dittus的以下示例 将IRC(Internet中继聊天)通信行为中的数据可视化,以查看谁在与谁讲话,以及谁在给谁命名。在这种可视化中,圆弧代表参考,而圆代表用户,圆的大小与该用户发送的消息数成正比,并且基于平均消息长度来着色。
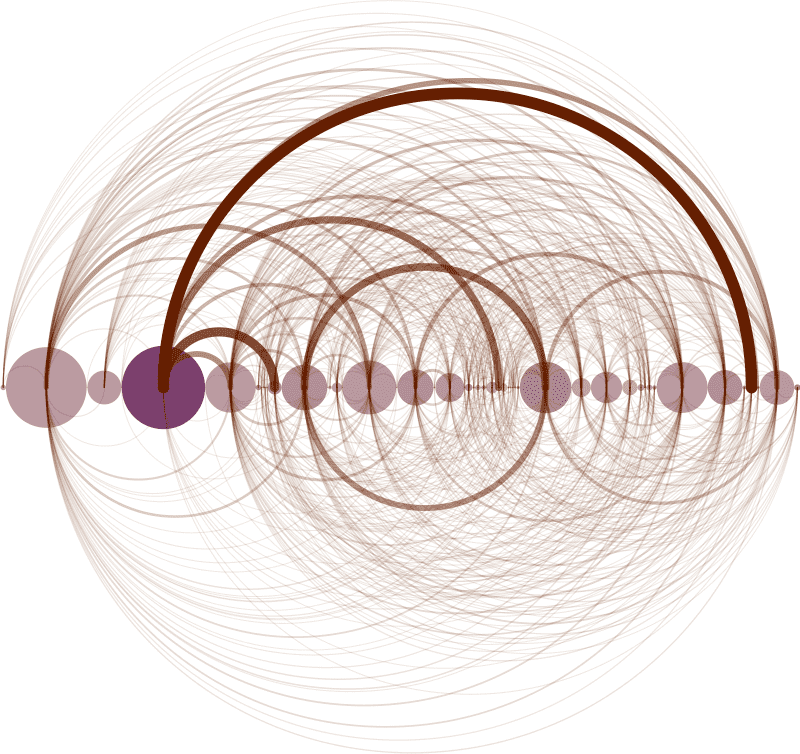
资料来源:IRC Arcs
32 +和弦图
可以通过在连接节点处放置形状区域来与弦图结合。在下面这个名为BeerViz的交互式示例中,用户可以通过连接线查看哪些啤酒彼此相似(基于参数:外观,香气,味道和总体评价)。圆圈的面积代表每种啤酒的受欢迎程度(基于用户评论的数量)。
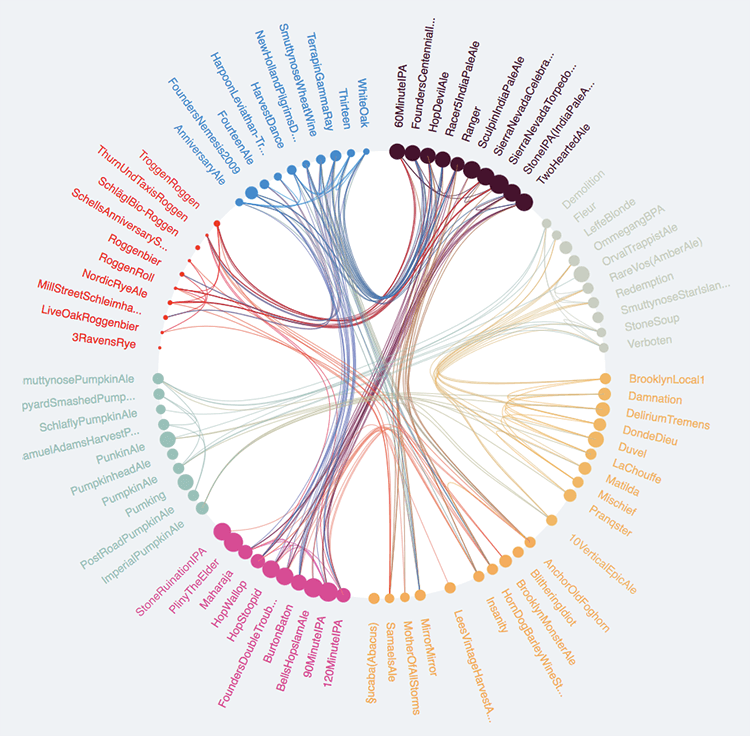
资料来源:BeerViz
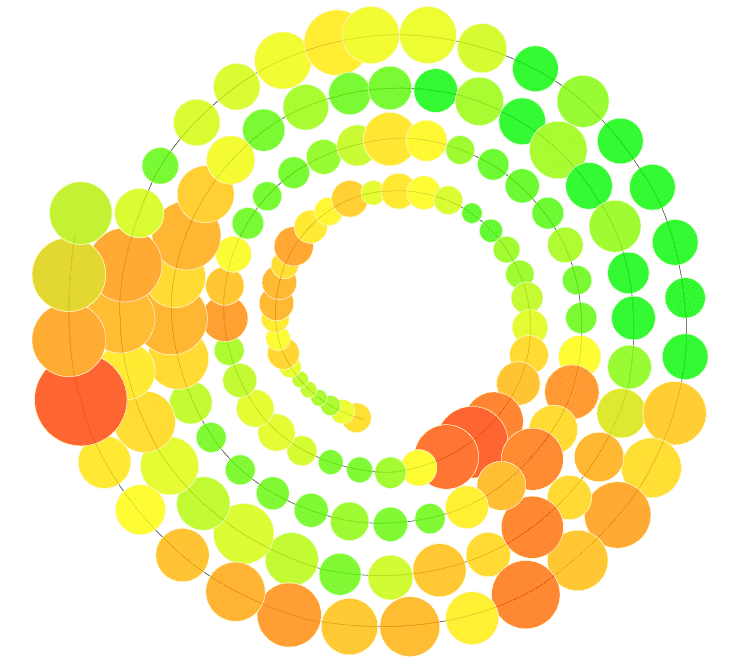
33 +螺旋图
我还没有看到的一种组合是螺旋图。这里的结构很简单:使用圆代替圆条,将其面积大小基于一个变量,并将颜色阴影基于第二个变量。
本文作者 @数据可视化那些事
版权声明
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符,请点击 举报 进行投诉反馈!
