正态分布在用户等级划分的应用

为了便于描述和应用，常将一般正态分布转化成标准正态分布。通过查标准正态分布表，就可以直接计算出原正态分布的概率值。

可知，3σ原则为：

1. 数值分布在（μ-σ,μ+σ)中的概率为0.6827
2. 数值分布在（μ-2σ,μ+2σ)中的概率为0.9545
3. 数值分布在（μ-3σ,μ+3σ)中的概率为0.9973

即x≥μ-σ的发生概率约84%，x≥μ发生概率约50%，x≥μ+σ发生概率约16%，x≥μ+2σ发生概率约为3%。

实践：

本例中要求划分为4个等级：

1. 第一步，取某足够长时间的播放数据；
2. 第二步，计算日人均播放时长（分）；
3. 第三步，计算日人均播放时长的平均值μ=62和标准方差σ=12.5；
4. 第四步，计算3σ分布。

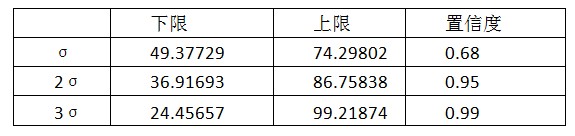
1. 第五步，得出各点的概率。

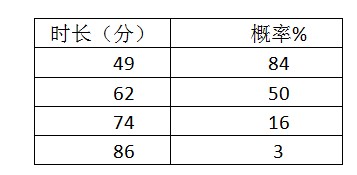
1. 第六步，计算最终时间，单位：分钟。

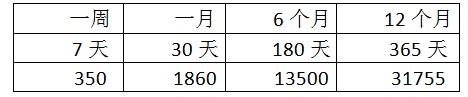
解释：

理论上来讲：

1. 84%的人一周后获得第一个等级；
2. 50%的人一个月后获得第二个等级；
3. 16%的人6个月后获得第三等级；
4. 3%的人12个月后获得第四个等级。

小结：

1. 第一个等级350分钟——即5.8小时；
2. 第二个等级1860分钟——即31小时；
3. 第三个等级13500分钟——即9.4天；
4. 第四个等级31755分钟——即22天。

展望：

由于一般的正态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x的概率，只要会用它求正态总体在某个特定区间的概率即可。

为了便于描述和应用，常将一般正态分布转化成标准正态分布。通过查标准正态分布表，就可以直接计算出原正态分布的概率值。

根据该理论可以实现任意等级的划分，只需将正态分布转为标准正态分布，根据每个等级可达到的概率进行查表获得相应的分界点。

作者 Vector

关键字：用户研究

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！