算法之神奇的斐波那契数列(Fibonacci sequence)

斐波那契数列

• 斐波那契数列的定义
• Fibonacci算法设计
• • 递归算法
  • 算法时间复杂度
  • 算法改进1
  • 算法优化2
• 斐波那契数列与黄金分割数
• 总结

14天阅读挑战赛
努力是为了不平庸~
数据结构+算法=程序。 数据结构是程序的骨架，算法是程序的灵魂。

斐波那契数列的定义

斐波那契数列可以用兔子数列来理解。
首先假设第一个月有一对初生兔子，第二个月进入成熟期，第三个月开始生育兔子，并兔子永不死去，它们按照下列的方式繁衍：

1. 第一个月，1号兔子没有繁殖能力，还是一对。
2. 第二个月，1号兔子进入成熟期，没有繁殖，还是一对。
3. 第三个月，1号兔子生一对兔子（2号），这个月有（1+1=）2对兔子。
4. 第四个月，1号兔子生一对兔子（3号），2号兔子进入成熟器，这个月有（1+2=）3对兔子。
5. 第五个月，1号兔子生一对兔子（4号），2号兔子生一对兔子（5号），3号兔子进入成熟器，这个月有（3+2=）5对兔子。
6. 第六个月，1号兔子生一对兔子（6号），2号兔子生一对兔子（7号），3号兔子进生一对兔子（8号），4号、5号 兔子进入成熟器，这个月有（3+5=）8对兔子。
   …

依此类推。
可以明显的看到：当月的兔子数=上个月兔子数+上上个月兔子数。

所以，不难看出，斐波那契数列是这样的：
$$1,1,2,3,5,8,13,21,34,55,...$$

递归表达就是：
F ( n ) = { 1 , n = 1 1 , n = 2 F ( n − 1 ) + F ( n − 2 ) , n > 2 F(n)=\left\{ \begin{aligned} 1,n & = 1 \\ 1,n & = 2\\ F(n-1)+F(n-2),n & > 2 \end{aligned} \right. F(n)=⎩ ⎨ ⎧​1,n1,nF(n−1)+F(n−2),n​=1=2>2​

Fibonacci算法设计

递归算法

设计递归算法实现斐波那契数列。

int Fibonacci(int n)
{if (n <= 0)return 0;if (n == 1 || n == 2)return 1;return Fibonacci(n - 1) + Fibonacci(n - 2);
}

测试代码：

#include 
#include int Fibonacci(int n)
{if (n <= 0)return 0;if (n == 1 || n == 2)return 1;return Fibonacci(n - 1) + Fibonacci(n - 2);
}int main(int argc,char **argv)
{int n = 6;if (argc > 1)n = atoi(argv[1]);printf("n= %d, Fibonacci: %d\n", n, Fibonacci(n));return 0;}

执行结果：

$ ./Fibonacci
n= 6, Fibonacci: 8$ ./Fibonacci 10
n= 10, Fibonacci: 55

算法时间复杂度

用$T(n)$表示Fibonacci(n)所需的基本操作次数，则：
n=1时，T(n)=1。
n=2时，T(n)=1。
n=3时，T(n)=3；调用Fib1(2)和Fib1(1)并执行一次加法运算（Fib1(2)+Fib1(1)）。

因此，n>2时，T(n)=T(n-1)+T(n-2)+1。它们的关系为：
F ( n ) = { 1 , n = 1 T ( n ) = 1 1 , n = 2 T ( n ) = 1 F ( n − 1 ) + F ( n − 2 ) , n > 2 T ( n ) = T ( n − 1 ) + T ( n − 2 ) + 1 F(n)=\left\{ \begin{aligned} 1,n & = 1 \space\space\space\space\space\space T(n)=1 \\ 1,n & = 2 \space\space\space\space\space\space T(n)=1\\ F(n-1)+F(n-2),n & > 2 \space\space\space\space\space\space T(n)=T(n-1)+T(n-2)+1 \end{aligned} \right. F(n)=⎩ ⎨ ⎧​1,n1,nF(n−1)+F(n−2),n​=1      T(n)=1=2      T(n)=1>2      T(n)=T(n−1)+T(n−2)+1​
由此可知：$T(n)\ge F(n)$。
斐波那契数列的通项公式：

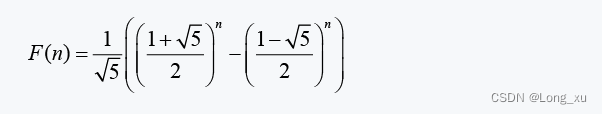
这里可以看到，时间复杂度属于爆炸增量函数。

算法改进1

int Fibonacci_1(int n) {int *F = new int[n + 1];//定义一个长度为n+1的数组，空间尚未使用F[1] = 1;F[2] = 1;for (int i = 3; i <= n; i++)F[i] = F[i - 1] + F[i - 2];return F[n];
}

这时，时间复杂度$O(n)$，空间复杂度$O(n)$。时间复杂度降下来了，算法效率有了重大突破，但是空间复杂度上去了。

算法优化2

上述算法优化使用了一个辅助数组记录中间结果，空间复杂度$O(n)$；其实只需要第n个斐波那契数，中间结果只是为了下一次使用，不需要保存。所以，可以采用迭代法进行算法优化：

int Fibonacci_2(int n){if(n==1||n==2)   return 1;int f1=1; int fs2=1;for(int i=3;i<=n;i++){int tmp=f1+f2;f1=f2;f2=tmp;}return f2;
}

使用三个辅助变量进行迭代，时间复杂度$O(n)$，但是空间复杂度降为$O(1)$。

斐波那契数列与黄金分割数

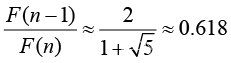
随着n趋向无穷大，斐波那契数列中前一项与后一项的比值越来越逼近黄金分割数0.618。

1 1 = 1 ， 1 2 = 0.5 ， 2 3 = 0.666 ， 3 5 = 0.625 ， . . . . . . ， 463681 75025 = 0.6180339886 \frac{1}{1}=1，\frac{1}{2}=0.5，\frac{2}{3}=0.666，\frac{3}{5}=0.625，......，\frac{463681}{75025}=0.6180339886 11​=1，21​=0.5，32​=0.666，53​=0.625，......，75025463681​=0.6180339886。

总结

1. 斐波那契数列起源于兔子数列，数学源于生活。斐波那契数列与黄金分割数有着千丝万缕的关系。
2. 算法难学的一个原因是算法本身具有一定的复杂性，需要持之以恒的学习和拓展自己的思维

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！