CCS之什么是频谱混叠
文章目录
- 序言
- 预备知识
- 复习傅里叶变换
- 拉式变换与傅里叶变换的关系
- 时域谱与频域谱之间的关系
- 什么是频谱混叠
- 时域上的理解
- 频域上的理解
序言
学数字信号处理的时候遇到频谱混叠,没有太在意,现在学计算机控制系统又遇到了它,所以我决定花点时间解决它,在开始前,我会先准备一些预备知识,主要有如下内容
- 复习傅里叶变换
- 拉氏变换与傅里叶变换的关系
- 时域谱与频域谱之间的关系
如果觉得自己的信号与系统基础比较薄弱,可以先去认真看看前面的预备知识,然后我会开始今天的正题,什么是频谱混叠。
预备知识
复习傅里叶变换
深入浅出地讲解傅里叶变换
拉式变换与傅里叶变换的关系
傅氏变换、拉式变换、Z变换之间的关系
时域谱与频域谱之间的关系
| 时域谱 | 频域谱 |
|---|---|
| 连续 | 非周期 |
| 离散 | 周期 |
| 周期 | 离散 |
| 非周期 | 连续 |
什么是频谱混叠
时域上的理解
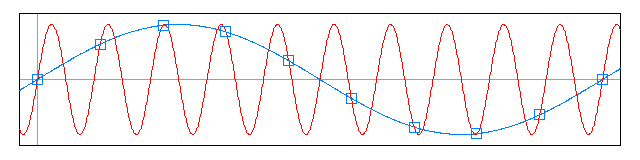
如上图所示,红色是真实地连续信号,蓝色小方框是我们地采样点,蓝色曲线是我们拟合出来地信号,很显然,由于采样频率过低我们无法还原出真实地信号,而是得到了一个低频信号,这就是频谱混叠在时域中地表现。
其实在日常生活中,频谱混叠地现象是很常见地,小时候有没有盯着屋顶地吊扇观察过,是不是感觉在反转,这是由于我们人眼的采样频率跟不上风扇地转速,本来是正转到 30 0 ∘ 300^{\circ} 300∘,结果我们以为是反转到 6 0 ∘ 60^{\circ} 60∘。
频域上的理解
首先明白一点:离散信号的频谱是原信号的频谱的周期延拓。
通俗一点说,离散信号的频谱是原信号的频谱左右搬移得到的,这个搬移量就是原始信号的采样频率,下面用一个例子来说明。
画出 5 e − 10 t 5e^{-10t} 5e−10t的时域图像和频域图像,傅里叶变换公式为 F ( w ) = ∫ − ∞ ∞ f ( t ) e − i ω t F(w)=\int_{-\infty}^{\infty}f(t)e^{-i\omega t} F(w)=∫−∞∞f(t)e−iωt
T=0.05
t=0:T:0.5
f=5*exp(-10*t)
subplot(2,1,1)
plot(t,f)
grid
subplot(2,1,2)
stem(t,f)
gridw=-50:1:50
F=5./sqrt(100+w.^2)
plot(w,F)
grid如下图所示
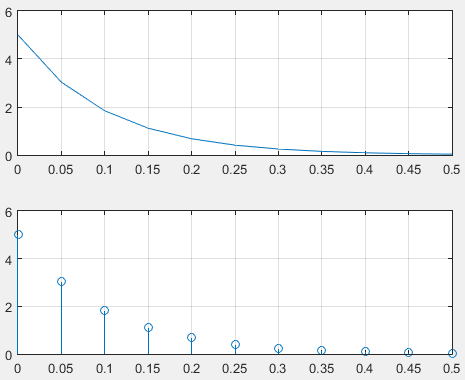
画出 5 e − 10 t 5e^{-10t} 5e−10t的离散傅里叶变换
w=-1000:20:1000
ws=200
Ts=2*pi/ws
F0=5/Ts*(1./sqrt(100+(w).^2))
F1=5/Ts*(1./sqrt(100+(w-ws).^2))
F2=5/Ts*(1./sqrt(100+(w+ws).^2))
plot(w,F0,w,F1,w,F2)
grid
w s w_s ws是采样频率,F0、F1、F2三个信号图像组合起来就是原始离散信号的部分频谱。我们可以看出,F1是F0右移得到,F2是F0左移得到。其中的Ts反应的是 w s w_s ws对离散信号频谱的幅度的影响,如下是上面的数据对应的频谱
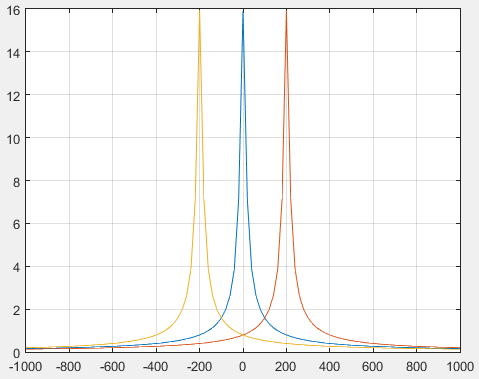
很明显,混叠严重,我们可以通过加大采样频率来减弱频谱混叠,如下所示
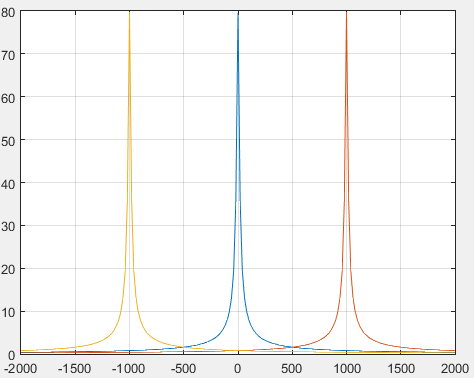
可以看出,改善了许多
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!