数字图像处理学习笔记3:图像的频域处理和滤波
本次学习内容是记录图像除了空域处理的另一个处理方式:频域处理,以及从频域角度看待滤波
目录
- 什么是频谱
- 空域-频域的变换
- 频域的滤波
1.什么是频谱
频域是指对于不同频率分量排列在一起,而不是按照时间或者位置作为坐标去衡量一些信号的域。
频谱则是在频域作为域去衡量的信号在不同频率下振幅大小的排列。
频谱可以反映变化,变化的越剧烈则高频成分越强,在整个区间内变化如果很小则说明频率值较小的部分占主要。(注意这里的占主要是指一个图像或者信号的频谱不是单一的,而是很多分量在不同的角度(频率值)构成的共同体。)
研究频谱和频域的原因是因为频域对信号的分析可以看做另一种模式,很多时候需要的是其中一部分稳定的分量,即固定的频率值的分量,如果在时域或者空间域中,时快时慢变化的信息会混杂在一起不便分离
2.空域-频域的变换
如果要从空间域变换到频率域,空间域的衡量单位是二维平面坐标。XY,确定的位置对应一个像素块,每个像素块对应的像素值是固定的。而在频域中只有一个坐标去衡量,即频率大小。
通过傅里叶变换可以让按照xy坐标变换的图像按照频率值变化而变化。
例如在原点处即频率为0的地方,计算公式为
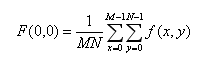
即f(x,y)的平均值,也就是说,如果f(x,y)是一幅图像,在原点的傅里叶变换等于图像的平均灰度值。因为在原点处常常为0,F(0,0)有时被称作频率谱的直流成分。
实际在用计算机实现的过程中多采用fft算法进行快速运算,得到其频谱的分布。

实现代码如下
import numpy as np
import matplotlib.pyplot as plt
import cv2
img = cv2.imread('p1-07.tif', 0)dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)# img表示输入的图片, cv2.DFT_COMPLEX_OUTPUT表示进行傅里叶变化的方法
dft_shift = np.fft.fftshift(dft)#将变化后的图像的低频转移到中心位置magnitude_spectrum = 20 * np.log(cv2.magnitude(dft_shift[:, :, 0], dft_shift[:, :, 1]))#返回幅值,取对数将数据变化到较小范围,*20使结果更大
#magnitud是计算二维矢量的幅值
plt.subplot(121), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()
变换后图像的中心点是低频成分,而周围则是高频。
3.频域的滤波
频域滤波顾名思义就是将部分不想要的频率分类过滤,得到需要的频率分类,一般频率是连续变化的,故频域滤波是对具体的频率段进行滤除。
比如:0-100的频率值中,我只想要较低的频率分量,可以用0-50的值为1,50-100的值为0的滤波器做对应相乘,此时高频段幅度为0,得到需要的结果。
import numpy as np
import cv2
import matplotlib.pyplot as plt
from scipy import fftpack
img = cv2.imread('p3-02.bmp', 0)
# =..
def low_pass_filter(img, radius=100):#对低通滤波器进行设定r = radiusrows, cols = img.shapecenter = int(rows / 2), int(cols / 2)mask = np.zeros((rows, cols, 2), np.uint8)x, y = np.ogrid[:rows, :cols]mask_area = (x - center[0]) ** 2 + (y - center[1]) ** 2 <= r * rmask[mask_area] = 1return mask
上面设定的一个低通滤波器为以图像中心为圆心,radius为半径的一个圆盘,内部区域mask定义赋值为1,外边为0。
def log_magnitude(img):#使显示更明显的变换函数magnitude_spectrum = 20 * np.log(cv2.magnitude(img[:, :, 0], img[:, :, 1]))return magnitude_spectrum
上述函数是将频谱由复数形式变换为实数,使其可以显示为二维图像。
img_dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
img_dft_shift = np.fft.fftshift(img_dft)
original_spectrum =log_magnitude(img_dft_shift)#原图频谱
mask = low_pass_filter(img, radius=30)
fshift = img_dft_shift * mask#频域的滤波
spectrum_after_filtering =log_magnitude(fshift)#滤波后频域图显示
上面是对频域变换和滤波,可以看到mask的大小设置为30,即半径30以内的频率都会被选出来,mask乘上把0移动到中心的频谱得到滤波后的频谱,移动再反变换得到滤波后图像,滤波后的频谱进行二维显示得到频谱图。

f_ishift = np.fft.ifftshift(fshift)
img_after_filtering = cv2.idft(f_ishift)#反变换
img_after_filtering =log_magnitude(img_after_filtering)#滤波后的图片
plt.subplot(2, 2, 1), plt.imshow(img, cmap='gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])#原图plt.subplot(2, 2, 2), plt.imshow(original_spectrum, cmap='gray')
plt.title('Spectrum of original image'), plt.xticks([]), plt.yticks([])#频谱图plt.subplot(2, 2, 3), plt.imshow(spectrum_after_filtering, cmap='gray')
plt.title('Spectrum after filtering'), plt.xticks([]), plt.yticks([])#滤波后频域图片plt.subplot(2, 2, 4), plt.imshow(img_after_filtering, cmap='gray')#滤波后的图片
plt.title('After filter or IFFT'), plt.xticks([]), plt.yticks([])plt.show()
上述显示代码注意第三行是要将滤波后的频谱反移动>反变换>求幅值
从结果可以看出,对滤波器增减大小也对滤波后的效果有影响,如果将半径radius变大,可以得到更多稍微高一点的频率,则不会过于模糊,如果radius减小,则会更模糊,但是噪声也会变少。
总结:频域对图片的影响在于:低频会让图像平滑,更模糊,高频会锐化,更注重边缘。低通滤波器可以用来滤除噪声,高通可以用来作边缘提取。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!