数据挖掘学习——数据预处理方法代码汇总（python）

目录

一、归一化处理方法

（1）min-max方法（离散归一化）

（2）零-均值规范化方法

（3）小数定标规范化

二、插值法

（1）拉格朗日插值法

三、相关性分析

（1）pearson相关性系数

（2）spearman相关性系数

四、主成分分析（PCA）

一、归一化处理方法

归一化常用方法有：

（1）min-max方法（离散归一化）

对原始数据的线性变换，将数据点映射到了[0,1]区间（默认）

一般调用sklearn库中的min_max_scaler函数实现，代码如下：

from sklearn import preprocessing
import numpy as npx =  np.array([[1972, 685, 507, 962, 610, 1434, 1542, 1748, 1247, 1345],[262, 1398, 1300, 1056, 552, 1306, 788, 1434, 907, 1374],])# 调用min_max_scaler函数
min_max_scaler = preprocessing.MinMaxScaler()
minmax_x = min_max_scaler.fit_transform(x)

（2）零-均值规范化方法

    把特征值的分布变化到均值为零。这种做法可以消除不同特征(或样本)之间的量级差异,使得特征之间的分布更加接近的变化,这在某些模型(如SVM)中,能够极大地提升处理效果,促使模型更加稳定,提升预测准确度。

代码实现：

import numpy as np
# 零-均值规范化
def ZeroAvg_Normalize(data):text=(data - data.mean())/data.std()return text

（3）小数定标规范化

小数定标规范化就是通过移动小数点的位置来进行规范化。小数点移动多少位取决于属性A的取值中的最大绝对值。

实现代码如下：

import numpy as np# 小数定标规范化
def deci_sca(data):new_data=data/(10**(np.ceil(np.log10(data.max()))))return new_data

二、插值法

在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。

插值是逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。

在图像的应用中，是填充图像变换时造成的空隙。

（1）拉格朗日插值法

在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值的一种插值多项式。

可以通过调用scipy库中的lagrange方法实现，代码如下：

'''拉格朗日插值法实现'''
from scipy.interpolate  import lagrange
import numpy as np
x_known = np.array([987,1325,1092,475,2911])
y_known = np.array([372,402,1402,1725,1410])
new_data = lagrange(x_known,y_known)(4)
print(new_data)

三、相关性分析

（1）pearson相关性系数

协方差除以标准差的乘积，pearson相关系数是线性相关关系，pearson相关系数呈现连续型正态分布变量之间的线性关系。

调用corr()方法，定义参数为pearson方法即可实现，代码如下：

# pearson相关系数计算
corr_pearson = df.corr(method='pearson')

（2）spearman相关性系数

秩（有序）变量之间的Pearson相关系数，spearman相关系数呈现非线性相关，spearman相关系数不要求正态连续，但至少是有序的。

# spearman相关系数计算
corr_spearman = df.corr(method='spearman')

四、主成分分析（PCA）

主成分分析（Principal Component Analysis，PCA）， 是一种统计方法，通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

在数据预处理中，我们常用PCA的方法对数据进行降维处理，将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

具体实现步骤如下：

1）首先对数据进行标准化，消除不同量纲对数据的影响，标准化可采用极值法

及标准差标准化法。

2）根据标准化数据求出方差矩阵。

3）求出共变量矩阵的特征根和特征变量，根据特征根，确定主成分。

4）结合专业知识和各主成分所蕴藏的信息给予恰当的解释。

可以直接调用sklearn中的pca方法实现，代码如下：

# 调用sklearn的PCA
from sklearn.decomposition import PCA
import numpy as np
import pandas as pddf=pd.DataFrame({'能力':[66,65,57,67,61,64,64,63,65,67,62,68,65,62,64],'品格':[64,63,58,69,61,65,63,63,64,69,63,67,65,63,66],'担保':[65,63,63,65,62,63,63,63,65,69,65,65,66,64,66],'资本':[65,65,59,68,62,63,63,63,66,68,64,67,65,62,65],'环境':[65,64,66,64,63,63,64,63,64,67,64,65,64,66,67]})#调用sklearn中的PCA函数对数据进行主成分分析
pca=PCA()
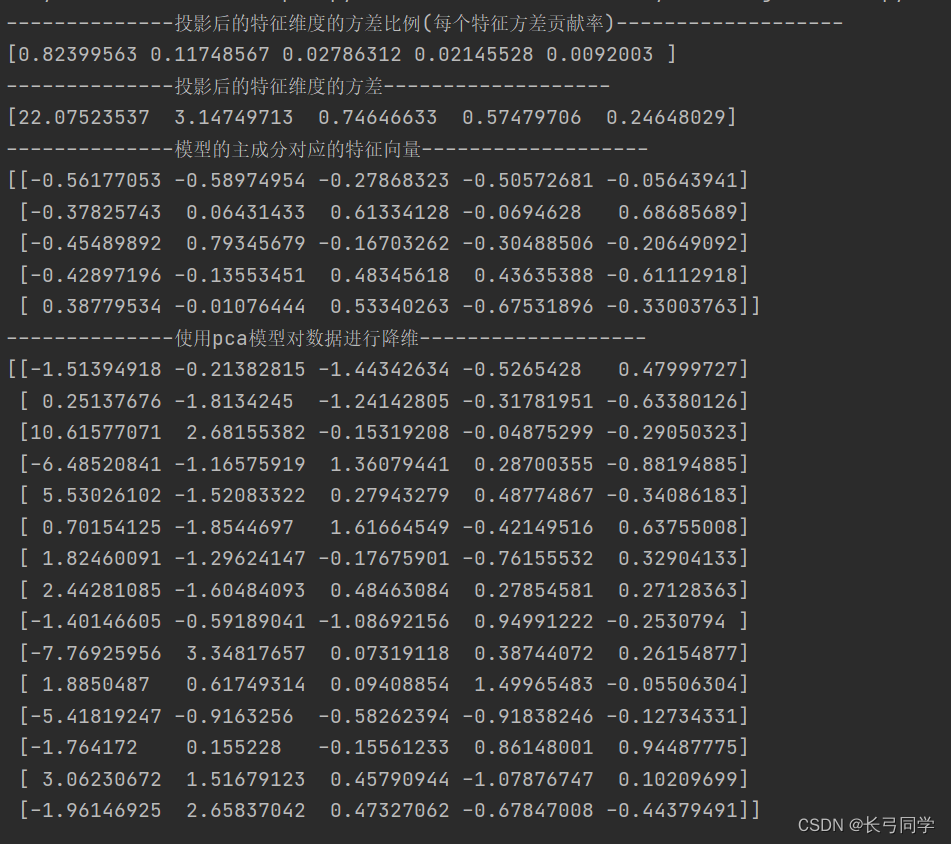
pca.fit(df) # 用训练数据X训练模型'''投影后的特征维度的方差比例'''
print('--------------投影后的特征维度的方差比例(每个特征方差贡献率)-------------------')
print(pca.explained_variance_ratio_)'''投影后的特征维度的方差'''
print('--------------投影后的特征维度的方差-------------------')
print(pca.explained_variance_)
print('--------------模型的主成分对应的特征向量-------------------')
print(pca.components_)
print('--------------使用pca模型对数据进行降维-------------------')
print(pca.transform(df))# 对数据进行降维

运行结果：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！