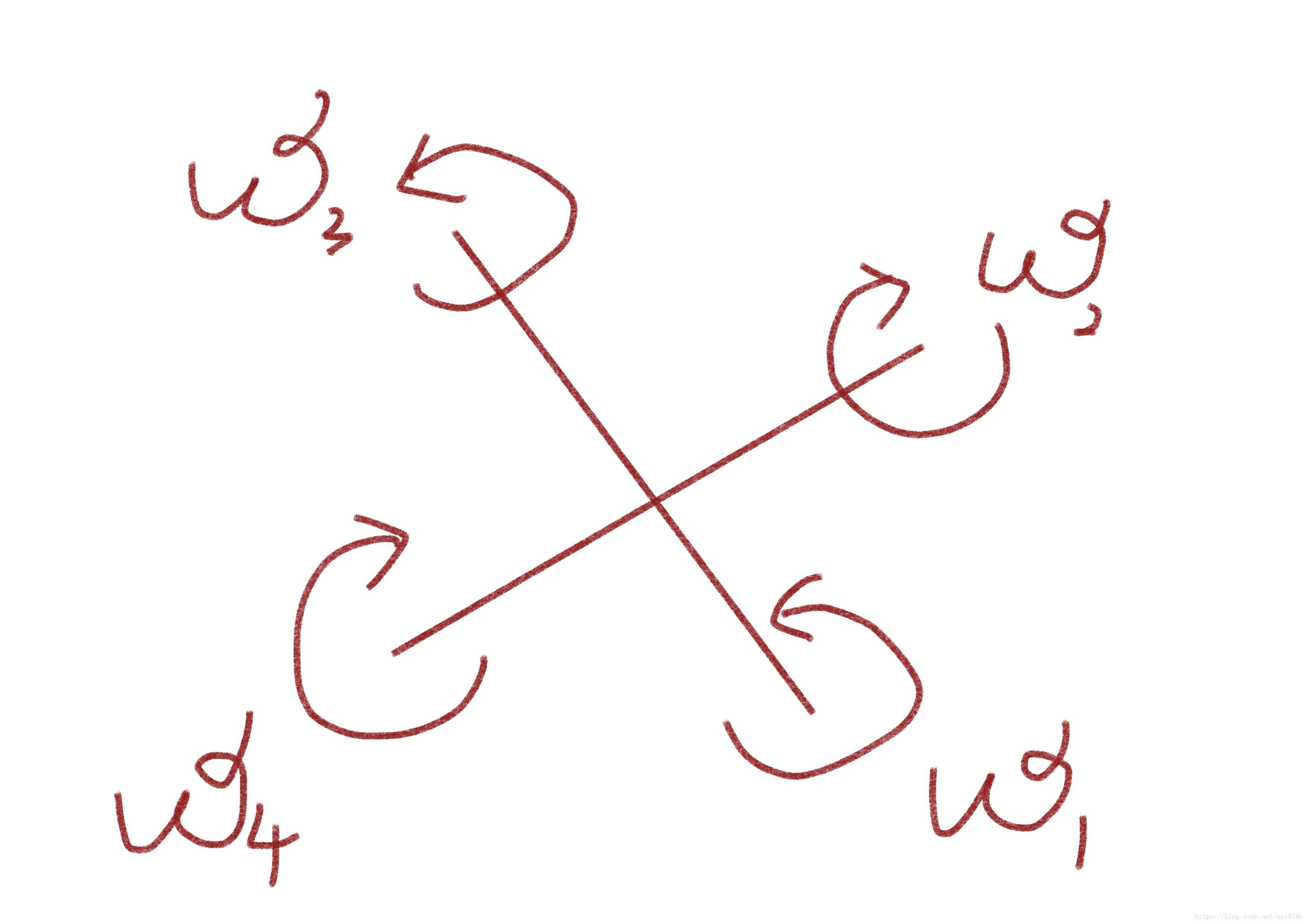cousera Aerial Robotics 无人飞行器 笔记1

第一周 综述

写在前面

这个暑假花了大概整整一周时间拿到了课程的证书，本课程主要内容是四旋翼的系统设计和控制，本课程对于运动学和动力学的数学推导有着比较详细的介绍，并在编程作业中对四旋翼的控制和路径规划进行了仿真，前置课程主要是自动控制原理和理论力学，编程作业主要是用Matlab，目前还没有中文字幕。

由于作者水平有限，可能存在错误，还望指正。

各种各样的无人飞行器

• aerial robots | 空中机器人
• Unmanned Aerial Vehicles(UVA) | 无人机
• Remotely Piloted Vehicles(RPVs) | 遥控飞行器，课程中将其也归为无人机
• Drones | 最常见的无人机叫法
• Quadrotor | 四旋翼

这些无人飞行器中的微型飞行器主要包括固定翼，扑翼和旋翼几种，本课程主要研究旋翼机中的四旋翼。

为什么选择四旋翼作为教授对象？

因为四旋翼结构简单，桨叶短而硬，飞行器在忽然转向时，桨叶不会因为陀螺力矩而扑动，也因此，四旋翼的建模比较容易。

四旋翼如何控制其姿态和位置？

将四旋翼的四个旋翼顺时针标号为1，2，3，4，其1，3转子的转动方向为逆时针，2，4转子方向为顺时针。

滚转和俯仰

机体坐标系下，滚转是绕X轴的运动，俯仰是绕Y轴的运动，四旋翼通过改变相对的一对旋翼的转动速度来产生滚转和俯仰力矩。

偏航

机体坐标系下，偏航是绕Z轴的运动，比如要控制飞行器顺时针旋转，则2、4电机减速，1、3电机加速，即逆时针旋转的速度加大，产生偏航力矩。
实现自动飞行有哪些关键因素

• State Estimation 估计出飞行器当前的位置、速度和姿态等。
• Control 根据目标状态和当前状态，计算出电机指令。
• Mapping 绘制所在环境的地图（商业级四旋翼一般无此功能）。
  Planning 在已知外界环境和目标地点的情况下，规划出一条避障轨迹。

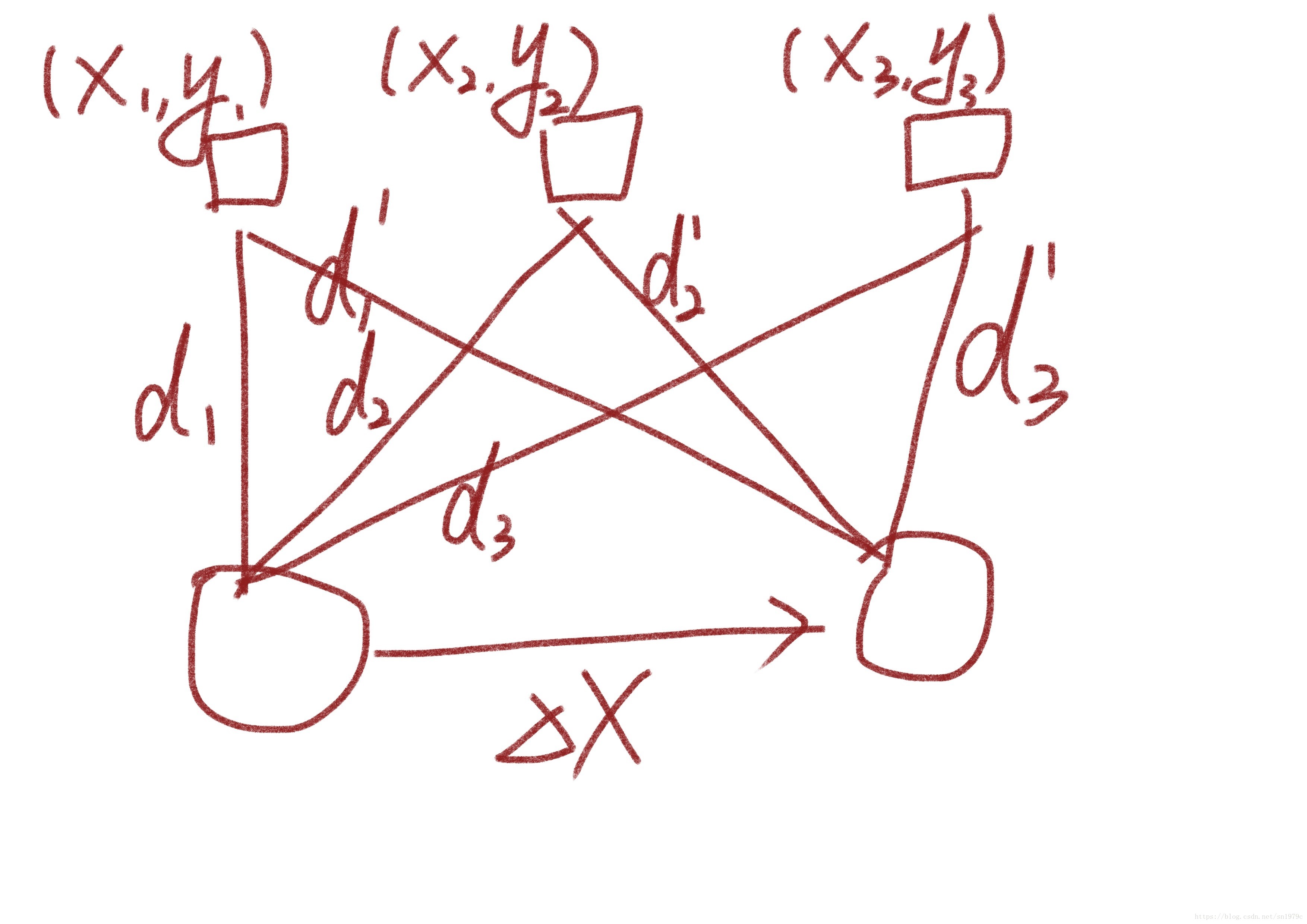
SLAM（Simultaneous Localization And Mapping）简介

SLAM也是当前人工智能中计算机视觉领域的一个热门方向，该问题可以表述为下：

机器人在未知环境中从一个未知位置开始移动，在移动过程中进行自身定位，并在自身定位的基础上建立环境地图，实现自主定位和导航。即同时实现Stae Estimation和Mapping。

SLAM问题如上图所示，已知 d 1 , d 2 , d 3 , d 1 ′ , d 2 ′ , d 3 ′ d_1,d_2,d_3,d_1',d_2',d_3' d1​,d2​,d3​,d1′​,d2′​,d3′​，同时估计 x 1 , x 2 , x 3 , δ x x_1,x2,x_3,\delta x x1​,x2,x3​,δx。

动力系统和系统设计

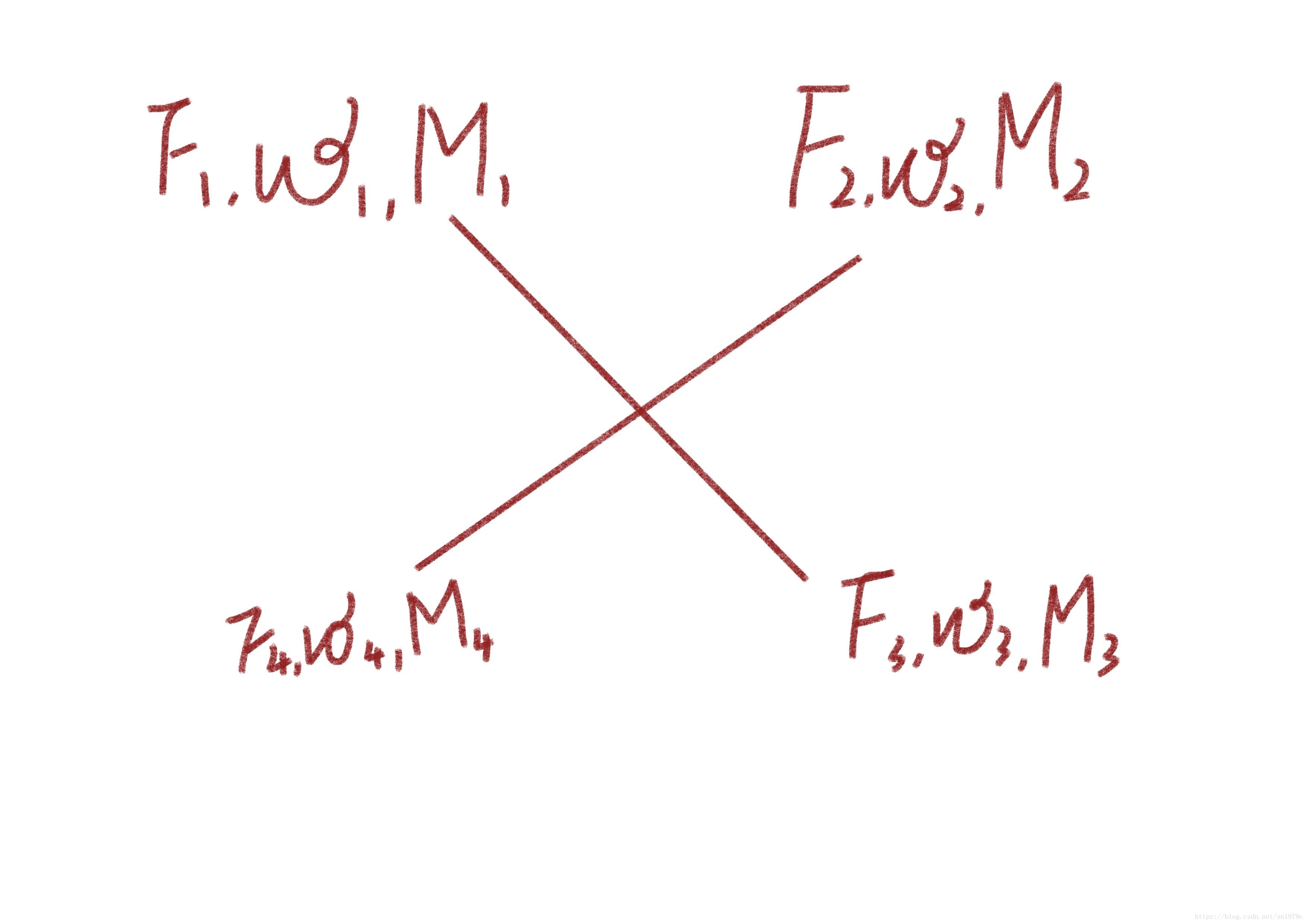
平衡方程

F = ∑ i = 1 4 F i − m g a 3 M = ∑ i = 1 4 r i F i + M i F = \sum_{i=1}^4{Fi}-mga_3 M = \sum_{i=1}^4{r_iF_i+M_i} F=i=1∑4​Fi−mga3​M=i=1∑4​ri​Fi​+Mi​

控制方程

PD控制

u ( t ) = x d e s + k v e ( t ) ( 1 ) u(t) = x^{des} + k_v e(t)^{(1)} u(t)=xdes+kv​e(t)(1)
当 k v > 0 k_v>0 kv​>0且 k p > 0 k_p>0 kp​>0时，系统稳定， k p k_p kp​增大，系统的超调量$\sigma$增大，反应更加迅速， k v k_v kv​增大，系统的阻尼增大。

PID控制

u ( t ) = x d e s + k v e ( t ) ( 1 ) + k i ∫ e ( t ) d t u(t) = x^des + k_ve(t)^{(1)} + k_i\int e(t)dt u(t)=xdes+kv​e(t)(1)+ki​∫e(t)dt
I项主要应对未知参数的扰动

设计上的一些考量

能量

四旋翼一般功率比重量的量级约为200W/Kg，固定翼约为120W/Kg，锂电池能提供的量级一般为400W/Kg。可以看出固定翼的效率比旋翼高近一倍。

机动性

yz平面内的四旋翼动力学模型

[ y ( 2 ) z ( 2 ) ϕ ( 2 ) ] = [ 0 − g 0 ] + [ − 1 m c o s ( ϕ ) 0 1 m c o s ( ϕ ) 0 0 1 I x x ] [ u 1 u 2 ] \begin{bmatrix} y^{(2)}\\z^{(2)}\\\phi^{(2)} \end{bmatrix} = \begin{bmatrix} 0\\-g\\0 \end{bmatrix} + \begin{bmatrix} -{1 \over m}cos(\phi)&0\\ {1 \over m}cos(\phi)&0\\ 0& 1 \over I_{xx} \end{bmatrix} \begin{bmatrix} u_1\\u_2 \end{bmatrix} ⎣⎡​y(2)z(2)ϕ(2)​⎦⎤​=⎣⎡​0−g0​⎦⎤​+⎣⎡​−m1​cos(ϕ)m1​cos(ϕ)0​00Ixx​1​​⎦⎤​[u1​u2​​]
u 1 u_1 u1​为所有旋翼的合拉力， u 2 u_2 u2​为所有旋翼的力矩

尺寸效应

l为四旋翼的臂长，r为旋翼的半径，m为四旋翼的质量。

Froude scaling

$m$ ~ y 3 y^3 y3

$F$ ~ π r 2 ∗ ( ω r ) 2 \pi r^2 * (\omega r)^2 πr2∗(ωr)2 ~ l 2 v 2 l^2v^2 l2v2

$M$ ~ $Fl$ ~ l 3 v 2 l^3v^2 l3v2

$\alpha$ ~ $M\over I $ ~ v 2 / l 2 v^2 / l^2 v2/l2

$v$ ~ l 1 / 2 l^{1/2} l1/2

Mach Scaling

$v$ ~ $1$

$F$ ~ $l$

$a$ ~ $1/l$

$\alpha$ ~ 1 / l 2 1/l^2 1/l2

结论

尺寸越小越敏捷

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！