c语言——实现单纯形法求解非线性规划问题

c语言——实现单纯形法求解非线性规划问题

提示：c语言，单纯形法，求解非线性规划问题，

一、单纯形法（simplex method）概念

Dantzing在1949年提出的单纯形法（simplex method）是一种行之有效的方法。
基本自想是：
从一个基本可行解出发，求出使目标函数值下降的另一个基本可行解。因此需要解决三个问题：
（1）求（LP）的初始基本可行解的方法；
（2）判别一个基本可行解是否为最优解的准则；
（3）从一个基本可行解转换到使目标数值下降的另一个基本可行解的方法。

二、算法步骤

（1）将线性规划化为标准型
（2）用最快的方法确定一个初始基本可行解X（0）。当s·t均为“≤”形式时，以松驰变量做初始基本变量最快。
（3）求X（0）中非基本变量xj的检验数σj。若，则停止运算，X（0）=X*（表示最优解），否则转下一步。
（4）
①由确定xk进基；
②由确定xl出基，其中alk称为主元素；
③利用初等变换将alk化为1，并利用alk将同列中其它元素化为0，得新解X（1）。
（5）返回（3），直至求得最优解为止。

三、流程图

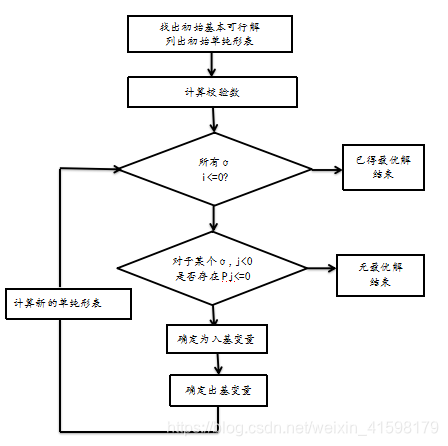
四、例题：

题目：求解线性规划问题。

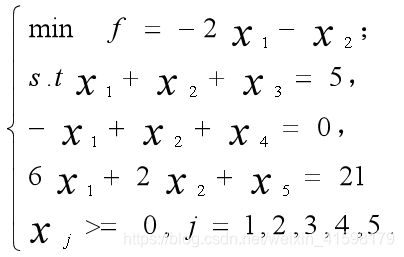
代码如下：

#include
#include
#define m 3 /*定义约束条件方程组的个数*/
#define n 5 /*定义未知量的个数*/
float M=1000000.0;
float A[m][n];   /*用于记录方程组的数目和系数;*/
float C[n];      /*用于存储目标函数中各个变量的系数*/
float b[m];      /*用于存储常约束条件中的常数*/
float CB[m];    /*用于存储基变量的系数*/
float seta[m];    /*存放出基与入基的变化情况*/
float delta[n];    /*存储检验数矩阵*/
float x[n];       /*存储决策变量*/
int num[m];     /*用于存放出基与进基变量的情况*/
float ZB=0;     /*记录目标函数值*/
void input();
void print();
int danchunxing1();
int danchunxing2(int a);
void danchunxing3(int a,int b);
int danchunxing1()
{
int i,k=0;
int flag=0;
float max=0;
for(i=0;i<n;i++)
if(delta[i]<=0)
flag=1;
else {flag=0;break;}
if(flag==1)
return -1;
for(i=

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！