小菜的算法学习笔记--初学者篇:算法图解 第六,七章--广度优先搜索、狄克斯特拉算法
小菜的算法学习笔记–初学者篇:算法图解 第六,七章
第六章:广度优先搜索
几个概念:
-
图:模拟一组链接,由节点和边组成。如地铁路线,朋友圈等,可以用图来表示。
-
最短路径:如下图从找到从双子峰到金门大桥的换乘最少次的路线
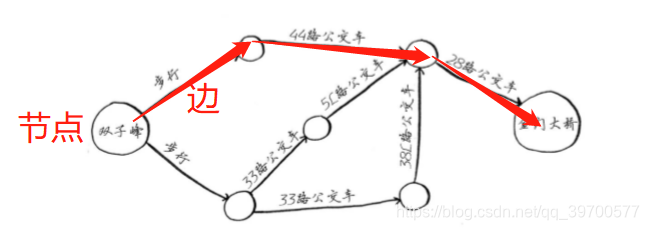
-
队列:先进先出的数据结构(与栈不同,栈是先进后出)
广度优先搜索:
可以回答两类问题:
第一类问题:从节点A出发,有前往节点B的路径吗?
第二类问题:从节点A出发,前往节点B的哪条路径最短?
例:找到朋友圈离我最近的卖茶女(属于第一类问题)
算法流程:
- 创建一个队列,储存要检查的人(好友)
- 从队列从取出第一个,检查ta是否为卖茶女
- 如果是,则找到了,如果不是,则把ta的好友加入队列中。
重复2,3步直到找到卖茶女。
from collections import deque #声明,python中用deque生成队列
def person_is_maicha(person):#定义判断函数,假设她叫miss teareturn person=="miss tea"
def search(name):#查找函数search_queue = deque() #用deque生成队列search_queue += graph[name]#将第一个节点直接连接的节点加入队列searched = []while search_queue: person = search_queue.popleft()#取出 if person_is_maicha(person): #判断print(person + " is a cheater!") return True else: search_queue += graph[person] #如果不是,把ta的好友加入队列searched.append(person)print(" no cheater!") return False
graph = {} #定义一个图
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny","miss tea"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = [] #定义结束
search("you") #测试运行时间为O(节点数+边数)
有顺序的图称之为树,例如家谱,是单向的
第七章:狄克斯特拉算法
如果给A到B的路加上时间,将问题变成寻找最快路径:
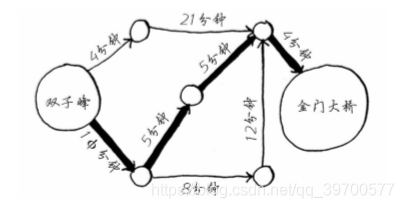
则可以采用狄克斯特拉算法:
- 跳到“最便宜”的节点
- 更新该节点的邻居,检查是否有前往它们的更短路径(计算其他路径的开销),如果有,就更新其开销。
- 重复1,2得到最终路径
一些概念:
权重:消耗;加权重的图:加权图;没加权重的图:非加权图
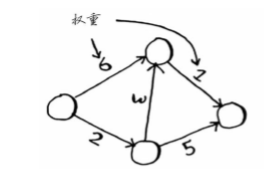
环:
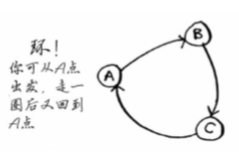
狄克斯特拉算法只适用于有方向的无环图。
代码实现:
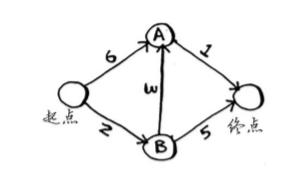
找到图中的最快路径:
def find_lowest_cost_node(costs) :#定义找到最快路径的函数lowest_cost = float("inf") lowest_cost_node = None for node in costs: cost = costs[node] if cost < lowest_cost and node not in processed: lowest_cost = cost lowest_cost_node = node return lowest_cost_node graph={}#定义加权图
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["b"] = {}
graph["b"]["a"]=3
graph["b"]["end"]=5
graph["a"] = {}
graph["a"]["end"]=1
graph["end"] = {}infinity = float("inf")
costs = {} #用散列表定义初始损失,开始到其他所有点的损失。不直接连接的点设为无穷(infinity)
costs["a"] = 6
costs["b"] = 2
costs["end"] = infinity parents = {} #用一个散列表储存父点(起始点),便于最后查找
parents["a"] = "start"
parents["b"] = "start"
parents["end"] = Noneprocessed = [ "start" ] #储存处理过的节点node = find_lowest_cost_node(costs) #查找初始消耗最少的点
while node is not None:#用while循环处理直到所有节点被处理后结束 cost = costs[node] neighbors = graph[node] for n in neighbors.keys():#python中用xxx.key()获得起点邻居 new_cost = cost + neighbors[n] if costs[n] > new_cost: #如果当前节点更近,则更新costs[n] = new_costparents[n] = nodeprocessed.append(node)node = find_lowest_cost_node(costs)print(parents)#从父节点可以倒推路径拓展:如果有负权边,即权重为负,则狄克斯特拉算法将失效,此时可用贝尔曼-福德算法:
个人理解,狄克斯特拉算法每次只针对当前节点的邻居进行最短路径的更新,而贝尔曼-福德算法则是遍历所有邻居的邻居,即从起始点开始每一次都保存从起始点到任意层节点的最短距离,直到到达终点。–贝尔曼-福德通过牺牲计算速度来保证不受负边影响。
详细可见:https://www.jianshu.com/p/e6a20905061c
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!