【笔记】算法图解

文章目录

• • 0 写在前面
  • 1 算法简介
  • • 1.1 引言
    • 1.2 二分查找
    • 1.3 大O表示法
    • • 常见的大O运行时间
      • 旅行商问题
  • 2 选择排序
  • • 2.1 内存的工作原理
    • 2.2 数组和链表
    • 2.3 选择排序
  • 3 递归
  • • 3.2 基线条件与递归条件
    • 3.3 栈
  • 4 快速排序
  • • 4.1 分而治之
    • 4.2 快速排序
  • 5 散列表
  • 6 广度优先搜索
  • • 6.1-6.2 图
    • 6.3 BFS
  • 7 狄克斯特拉算法
  • 8 贪婪算法
  • • NP完全问题
    • 如何判断是否NP完全
  • 9 动态规划
  • 10 K最近邻算法
  • 11 接下来如何做

0 写在前面

本书对于算法概念解释比较详尽，印象比较深的就是用图形象地比较出了数组与链表的区别，但是对算法的原理概念介绍并不是特别多的内容，只起到一个启蒙的作用，建议作为闲暇书籍或增强自信之用，笔者阅读时长约三个小时。

以下是笔者对于此书的简要笔记，个人风格浓厚，谨慎食用。

鉴于版权原因，如需要原书资源可评论，代码见github(不完全，因为简单所以懒得写了，有需要我会补充，欢迎评论)。

1 算法简介

1.1 引言

算法即一组完成任务的指令，任何代码片段都可视为算法。但本书只讲一部分，介绍的算法要么速度快，要么能解决有趣的问题，要么兼而有之。

1.2 二分查找

以最少字数猜数字为例，从1开始依次往上猜叫简单查找

二分查找即中学时代学的二分法，略

运行时间：对于包含n个元素的列表，用二分查找最多需要log2n步，而简单查找最多需要n步。

注意：仅当列表是有序的时候，二分查找才管用。

1.3 大O表示法

大O表示法即表示算法有多快。定义如下，假设列表包含n个元素。简单查找需要检查每个元素，因此需要执行n次操作。使用大O表示法，这个运行时间为O(n)。又比如对于上面的二分查找则是O(log n)
注意，大O表示法指最糟情况下的运行时间，且并不以秒为单位。

常见的大O运行时间

$O(logn)$，也叫对数时间，这样的算法包括二分查找。
$O(n)$，也叫线性时间，这样的算法包括简单查找。
$O(n\ast logn)$，比如第4章将介绍的快速排序——一种速度较快的排序算法。
O ( n 2 ) O(n^2) O(n2)，这样的算法比如第2章将介绍的选择排序——一种速度较慢的排序算法。
$O(n!)$，这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。

旅行商问题

略，可谷歌

2 选择排序

2.1 内存的工作原理

写入或存储数据时，需请求计算机提供存储空间，计算机会给一个存储地址，而存储多项数据时，有两种基本方式：数组和链表

2.2 数组和链表

数组必须出于一段连续的内存地址，而链表可以在任意地方。

数组的缺点在于如果要添加新元素可能空间不够难以转移，即便预留空间也可能浪费内存，而链表相应在插入元素方面颇具优势，需要中间插入元素时，链表更好，删除元素也是

但是链表只访问中间或者最后一个元素时，必须先访问第一个元素，然后一直推到中间或者最后一个元素，效率比较低，而数组由于知道每个元素的地址就可以轻松访问

数组中元素的位置叫索引(index)

2.3 选择排序

给定一个数列按从大到小排序，可以先遍历列表找出最大数，并将其添加到新列表中，然后同理找出第二大的数，依次类推，这样需要的时间为 O ( n 2 ) O(n^2) O(n2)，这就是选择排序

3 递归

3.2 基线条件与递归条件

注意编写涉及数组的递归函数时，基线条件通常是数组为空或只包含一个元素。陷入困境时， 请检查基线条件是不是这样的。

3.3 栈

有基本调用栈和递归调用栈

4 快速排序

分而治之(divide and conquer，D&C)是一种著名的递归式问题解决方法，比如快速排序

4.1 分而治之

私以为类似于动态规划的思路，在划分土地这个例子中有"这小块地的最大方块，也是适用于整块地的最大方块"。

4.2 快速排序

具体原理可以百度，其运行时间在平均情况下为$O(n\ast logn)$，在最糟情况下为 O ( n 2 ) O(n^2) O(n2)。还有一种合并排序算法(merge sort)，其运行时间总是为$O(n\ast logn)$

快排的平均情况与最糟情况见原书4.3.2

5 散列表

即哈希表(hash)，python中的散列表实现就是字典

6 广度优先搜索

广度优先搜索是一种图算法(breadth-first search, BFS)，能够找出两样东西之间的最短距离，其含义有很多，如下：

• 编写国际跳棋AI，计算最少走多少步就可获胜

• 编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如将

  READED改为READER需要编辑一个地方

• 根据你的人际关系网络找到关系最近的医生

6.1-6.2 图

图由节点和边组成，一个节点可能与很多节点直接相连，它们称为邻居。

图分无向图与有向图，有向环形图与无向图等价，如下：

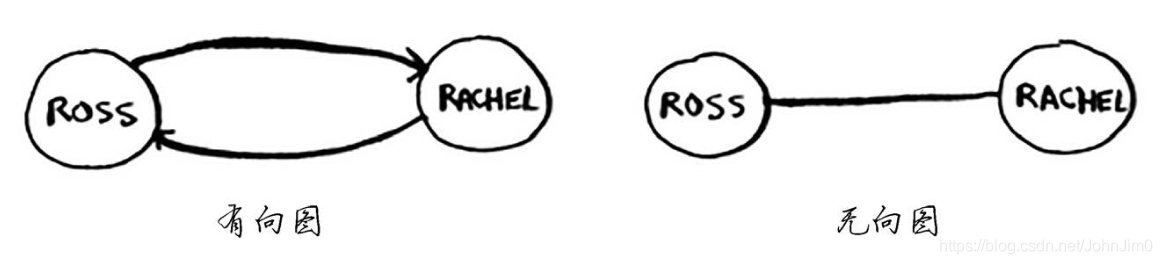
6.3 BFS

比如找到你的朋友最近的果商，先搜索所有你的朋友形成一度关系列表，然后搜索你的朋友的朋友形成二度关系列表，依次类推，直到找到果商或者遍历整个图为止，这就是广度优先搜索。

其运行时间为$O(V+E)$，V为图的人数或者说节点数，E为边数

7 狄克斯特拉算法

广度优先搜索只能找到总边数或者段数最少的路径，对于各边长不相同的图，如下：

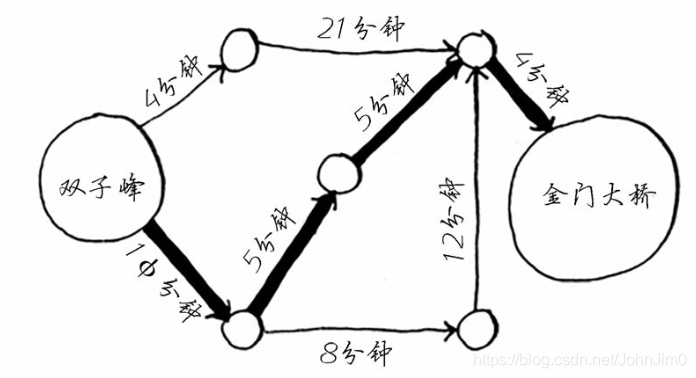
其边长有4分钟，5分钟等，此时需要用到狄克斯特拉算法。这种边长不一样或者边关联数字的，这些数字叫做权重，带权重的图为加权图，否则叫非加权图。另外注意狄克斯特拉算法只适用于有向无环图(directed acyclic graph，DAG)，并且需要权重为正。如果包含负权重，需使用贝尔曼福德算法。

迪克斯特拉算法原理可以谷歌。

但是，该算法是否一定能遍历到所有节点以至于终点？暂时还不明白

8 贪婪算法

与其说是一种算法，不如说是一种策略，即每步都选择局部最优解，最终得到的就是全局最优解。但是并非在任何情况下都行之有效，但是易于实现！

上面讲的快速排序不是贪心算法，而广度优先搜索和狄克斯特拉算法都是。

NP完全问题

比如旅行商问题，详解见原书

如何判断是否NP完全

如果判断一个问题是NP完全，就不用去找到精确解，而是使用近似解。

没有一个系统的办法判断是否是NP完全问题，但是也有一些蛛丝马迹可循：

• 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
• 涉及“所有组合”的问题通常是NP完全问题。
• 不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
• 如果问题涉及序列(如旅行商问题中的城市序列)且难以解决，它可能就是NP完全问题。 
• 如果问题涉及集合(如广播台集合)且难以解决，它可能就是NP完全问题。
• 如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题。

9 动态规划

动态规划的思路即将问题分解成各个子问题解决，具体难以理解，可通过实例一步步加深印象。

实例见原书

注意但仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用。

10 K最近邻算法

略，之前机器学习实战也有

本章也有机器学习简介，列举了OCR、垃圾邮件过滤器和预测股票市场三个实例

11 接下来如何做

列举了10种未介绍的算法，即

• 树
• 反向索引
• 傅立叶变换
• 并行算法
• MapReduce，一种特殊的并行算法，即分布式算法
• 布隆过滤器和HyperLogLog
• SHA 算法，主要用于加密，SHA-0、SHA-1、SHA-2和SHA-3，前两者已发现有缺陷，最安全的目前是bcrypt
• 局部敏感的散列算法，即Simhash
• Diffie-Hellman 密钥交换，其替代者有RSA
• 线性规划

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！