推荐策略产品经理必读系列—第五讲推荐系统的召回三

一、什么是向量召回

1. 向量

具有大小和方向的量。向量召回的核心思想就是将用户特征和物料特征全部用向量来表示，然后基于向量来计算用户与物料的相似度、用户与用户的相似度、物料与物料的相似度。

2. Embedding

何为Embedding？大家应该经常听到这个词，那么到底什么是Embedding了？Embedding翻译：“嵌入”& “向量映射”，是一种用一个数值向量“表示”一个对象（Object）的方法。Embedding可以理解为是一种编码方式，把相关字符类值比如“安徽”通过编码的方式转化为可以供计算机使用的数字。

下面我们用一个例子来先看一下基于向量的表达。

上图中一个用户有六个特征，分别是【年龄、性别、年薪、爱好、户籍、学历】，很多特征都是文本特征，计算机无法直接基于文本特征来计算两个用户之间的相似度，需要先把文本转化为向量，计算机最后基于向量计算出两个用户之间的相似度了。

二、隐语义模型

向量召回中最经典的应用也就是隐语义模型了，或者叫做隐向量模型，或者叫做矩阵分解模型。我们之前介绍了协同过滤思想，协同过滤思想有什么不好的地方了，隐语义模型对比协同过滤有什么先进之处了。

2.1 案例引入

首先我们通过一个生动的例子来回顾一下协同过滤的思想。某天吃货路飞走进了一家饭店进行点餐，服务员小薇上来服务：

1）Item-CF思想点餐

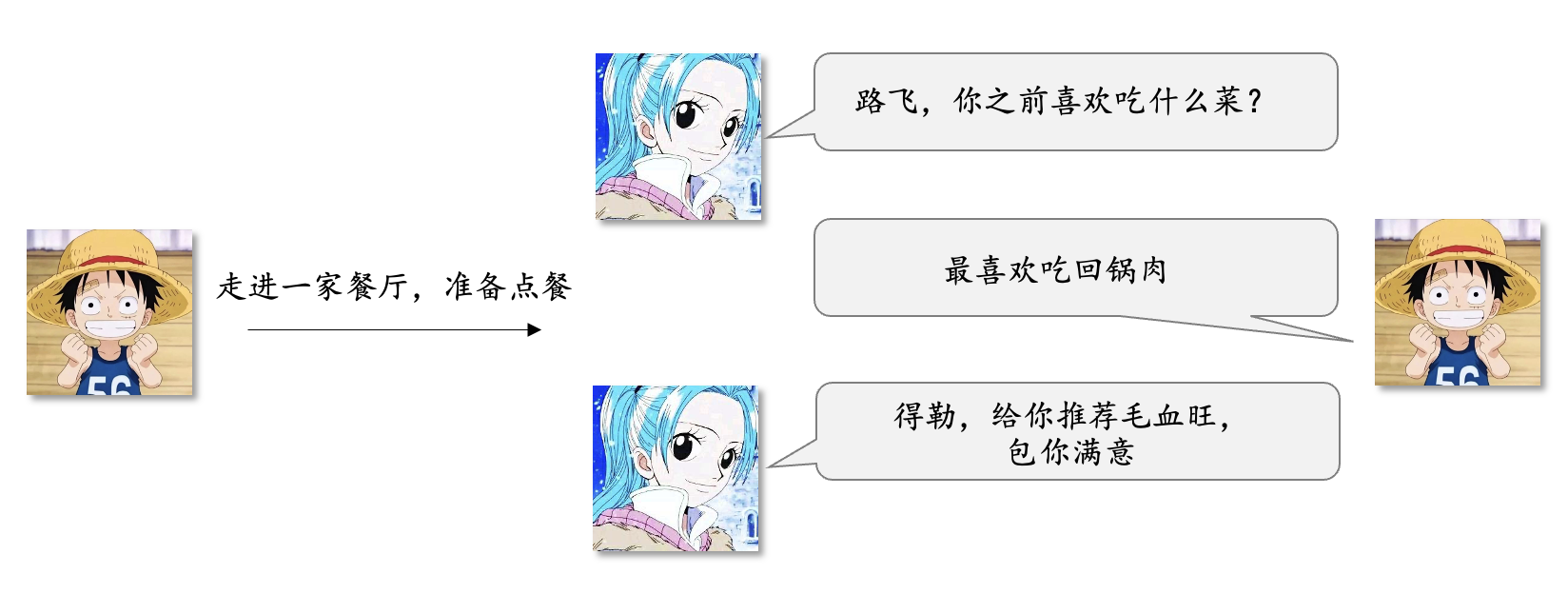
基于路飞之前吃过的菜，为其推荐相似的菜品。

2）User-CF思想点餐

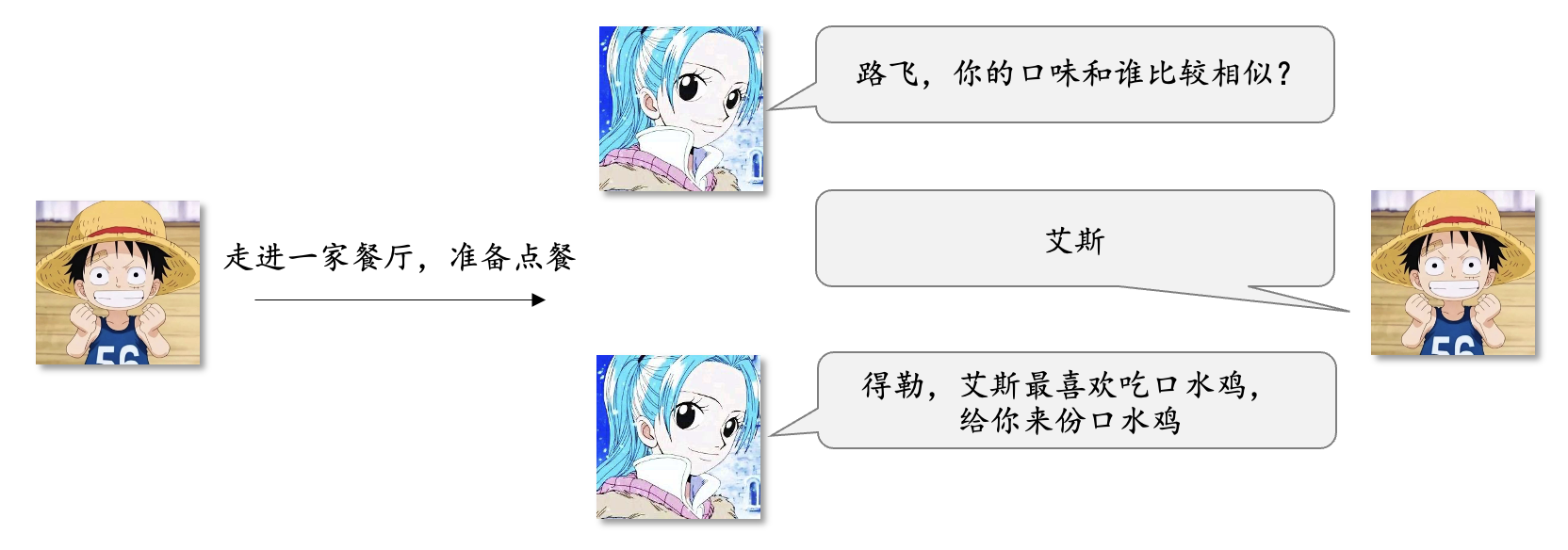
基于和路飞口味相同的人，为其推荐口味相同的人爱吃的菜。

3）隐语义思想点餐

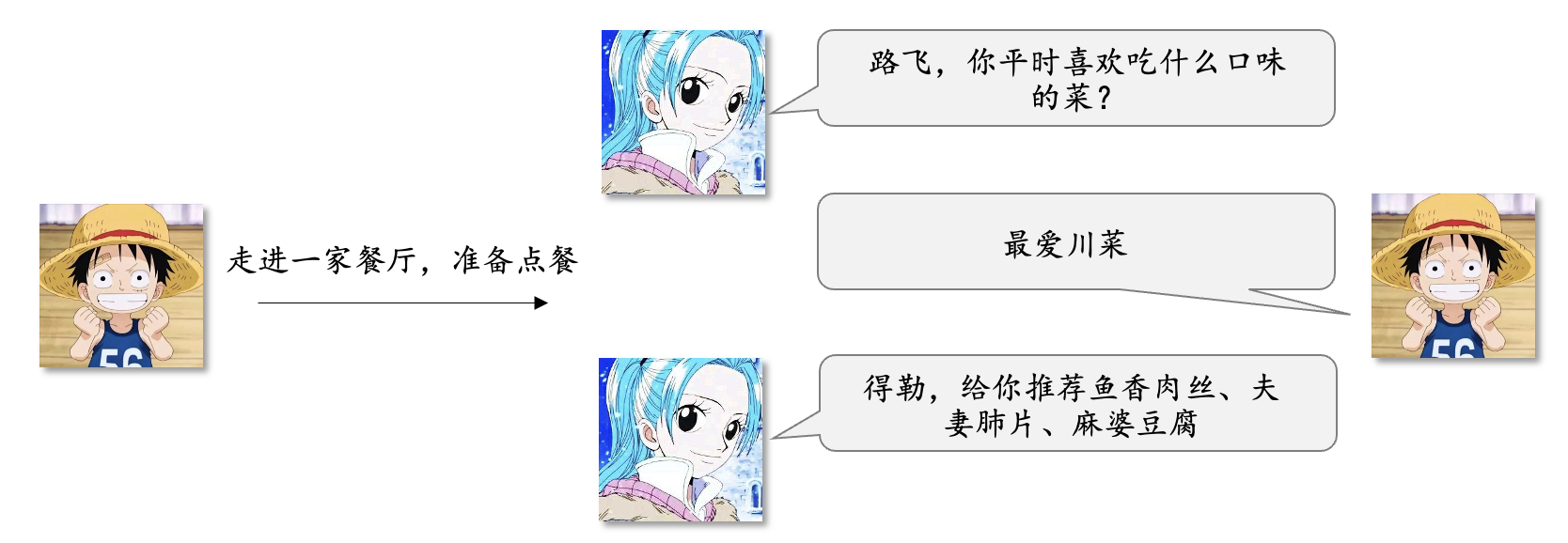
隐语义模型的思想是先确认User的兴趣偏好分类，然后将User的兴趣偏好分类和Item的分类对齐。各位读者也可以明显看得出来隐语义思想是一种更加贴近于我们实际生活，更加先进的思想。

我们用这么一张概括图片，大家就能够非常清晰地明白协调过滤思想和隐语义模型思想之间的差异了：

协同过滤是将物料和用户之间建立更多的链接，而隐语义模型的思想是将用户和物料归到相同的特征维度上，最后在相同的特征维度上进行相似度比较。

User-CF：首先找到和目标用户吃同样菜的其他用户，然后为目标用户推荐其他用户喜欢吃的菜；Item-CF：首先明确目标用户历史喜欢吃的菜，然后找到和历史喜欢吃的菜比较相似的新菜；

隐语义模型：首先明确目标用户的兴趣爱好，比如喜欢什么类型的菜，将用户的兴趣分类和菜的分类对齐，最后为其匹配符合其偏好的菜品；下面一个例子就是基于原始的用户对于物料的评分表，将用户和物料进行矩阵分解Embedding在相同的特征维度上。

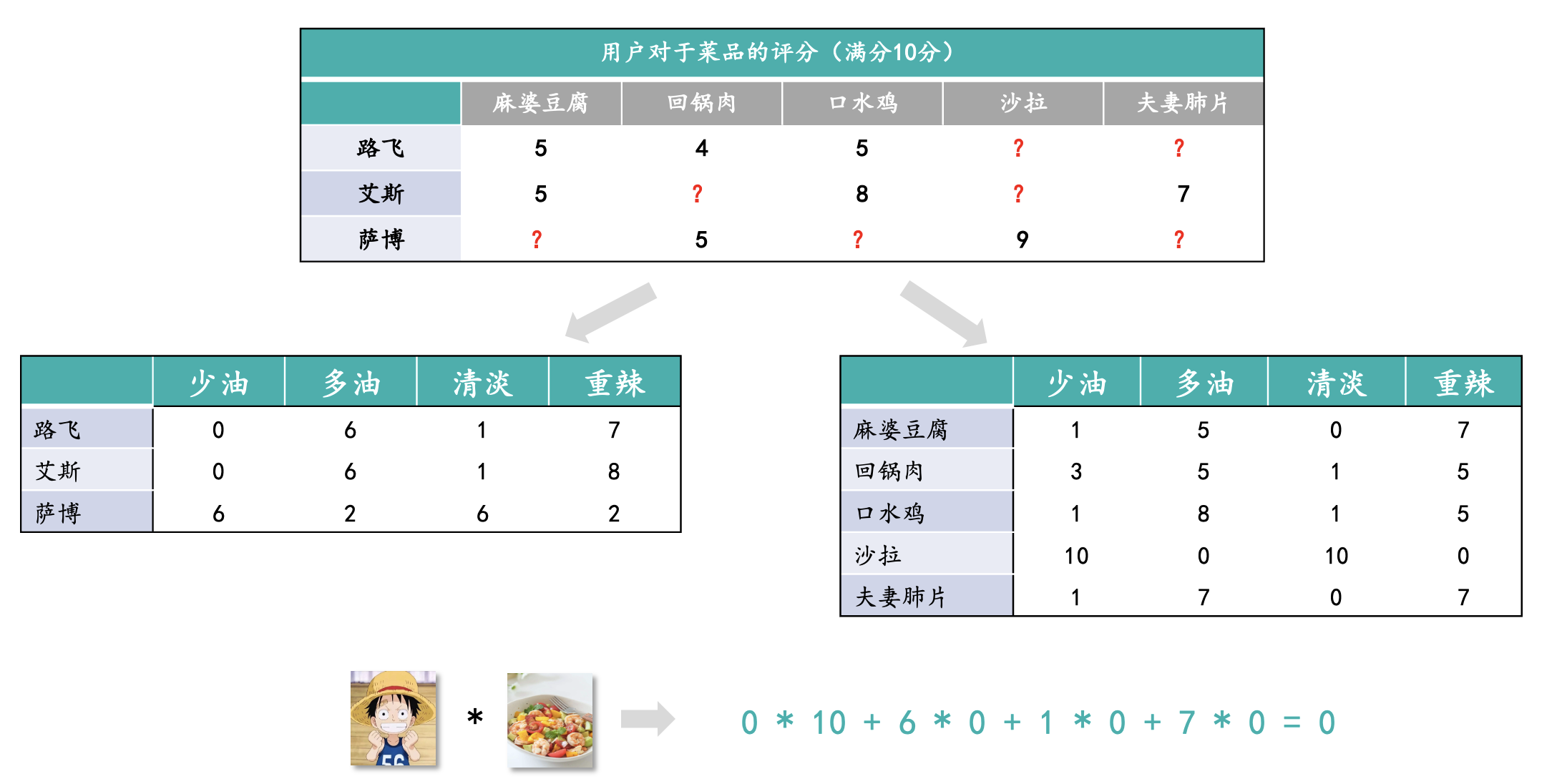
通过路飞和沙拉在相同维度下的匹配度，最后计算出路飞对于沙拉的偏好为0。

2.2 隐语义模型概述

我们对隐语义模型进行一个概述，日常我们经常听到的隐向量模型或者矩阵分解模型，它们的其实含义是一样的。

隐语义模型 or 隐向量模型 or 矩阵分解模型：通过用户的行为数据，挖掘出隐含的特征（Latent Factor），最终将用户与物料Embedding在相同维度的特征上，在相同维度下进行相似度计算。使用更稠密的隐向量表示用户和物品， 挖掘用户和物品的隐含兴趣和隐含特征。大家经常会看到Embedding这个词，翻译成中文叫做“嵌入”或者“向量映射”，实际就是将用户和物料的特征映射到某个特征空间用向量来表达的一种方法。

隐语义模型的核心就是如何将一个共现矩阵（用户和物料的交互矩阵）分解成两个小矩阵，也就是分解成一个用户矩阵和一个物料矩阵，其中两个小矩阵必须分解在相同的隐向量维度上，也就是下图中的K，两个小矩阵相乘可以变回原本的共现矩阵。

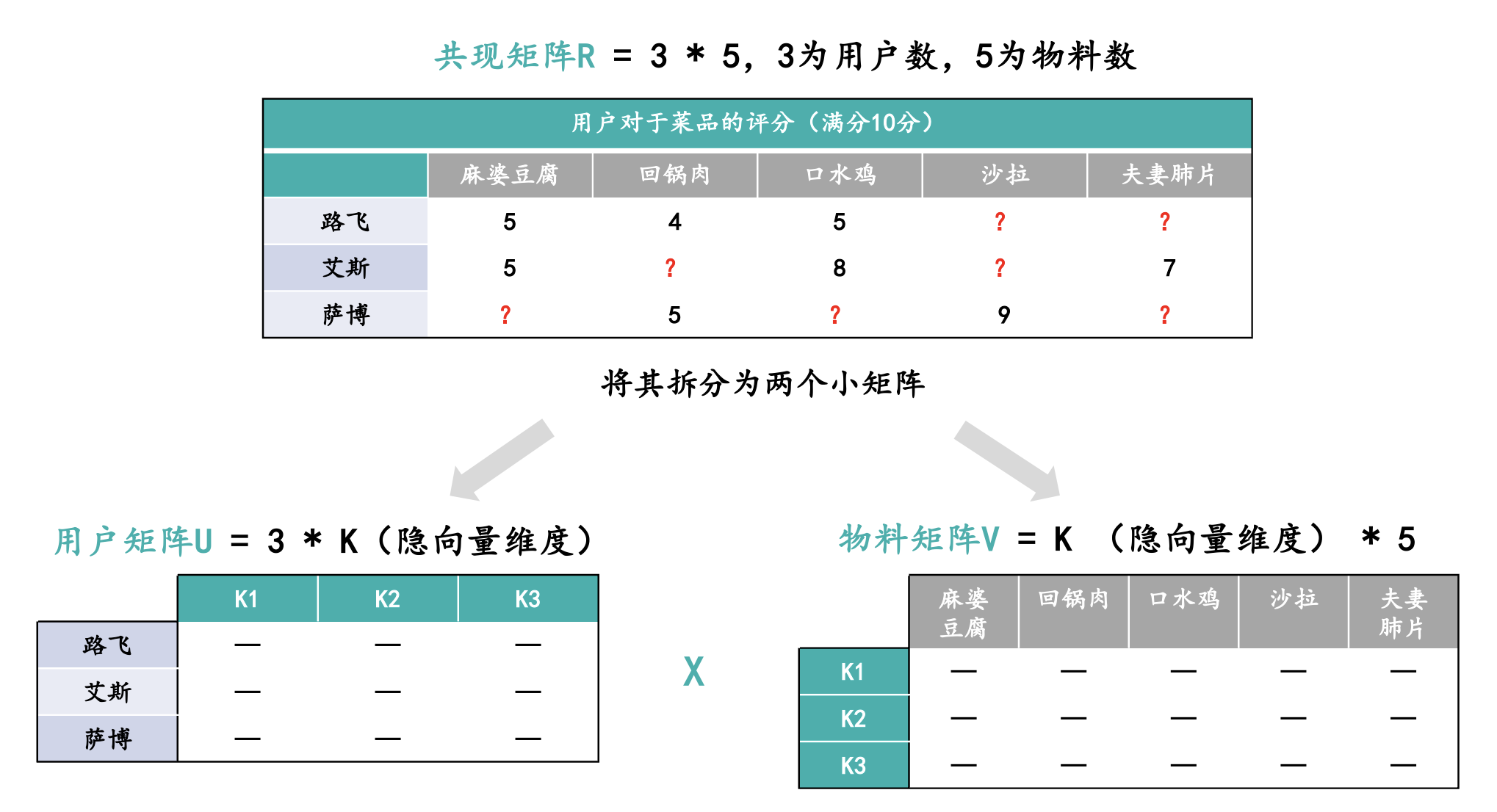
当我们将一个大矩阵分解成两个小矩阵时，面临两个核心问题，第一个核心问题是两个小矩阵公用的这个隐向量维度K怎么设置？K的维度设置为多少比较合适？

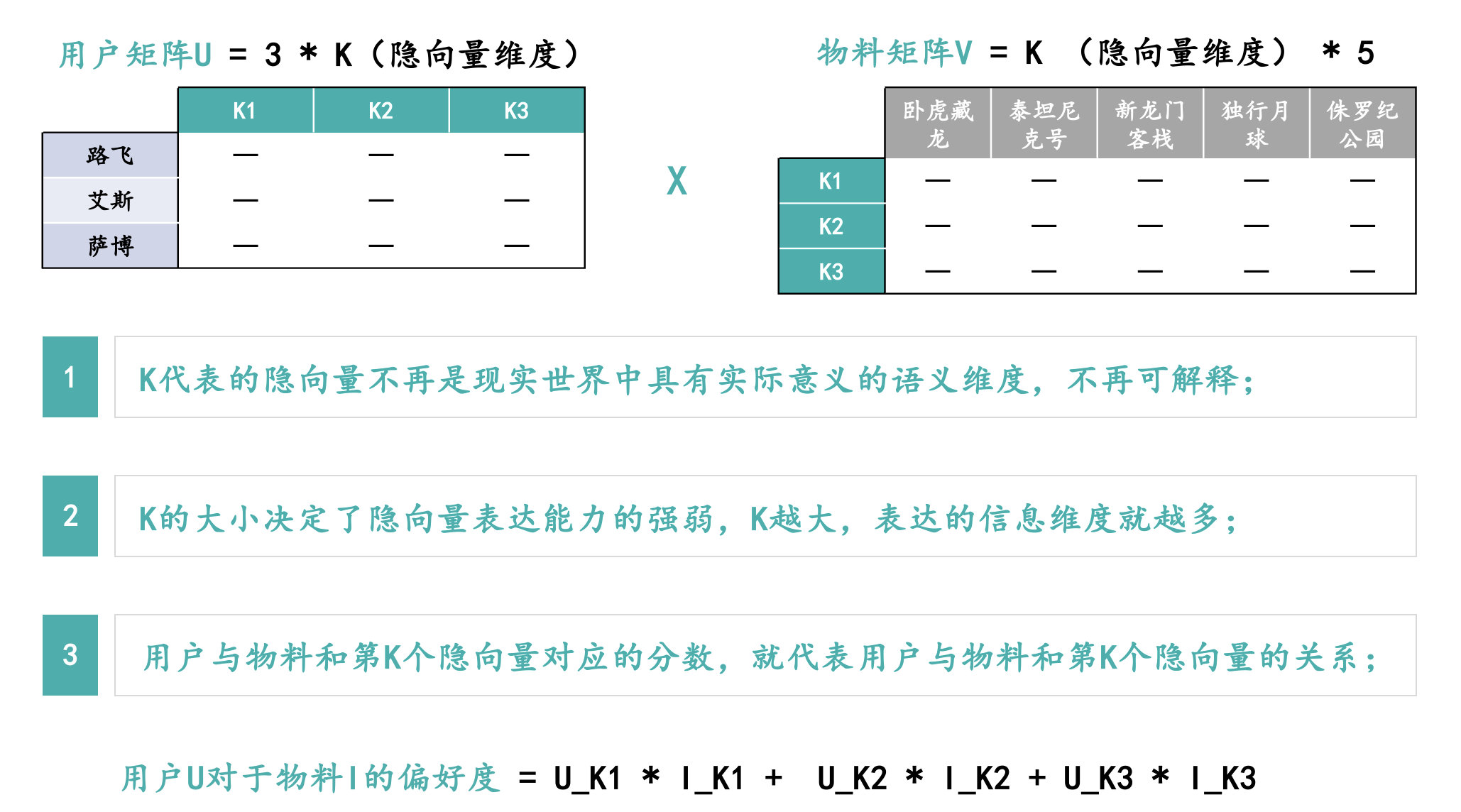
隐向量K维度的设置：

第一点：K代表的含义是什么？

K本身代表的隐向量维度不具有现实世界中的实际语义含义，不可解释。Part2.1里面的点餐案例用了一些大家都能够熟悉的语义进行举例，但实际在隐语义模型里隐向量都是不可解释的，也不具备实际的语义含义。

第二点：K是不是越大越好？

K本身并不是越大越好，K越大虽然表示的信息维度就会越多，但是泛化能力也会越差，K越大对于系统性能的要求以及算力要求也会越高；K越小表示的信息维度就会越少，但是泛化能力也会越强。最终K的取值是在模型效果和系统性能之间进行权衡利弊后做出的选择。

第三点：用户U对于物料I的偏好度如何计算？

用户U对于物料I的偏好度最终的计算其实就是将用户在第K个隐向量上的分数和物料在第K个隐向量上的分数进行相乘，最终将所有K维度的分数累加在一起。

2.3 矩阵分解

矩阵分解的第二个核心问题就是通过什么方法将一个大矩阵拆分成两个小矩阵，其实这本质是一个数学问题。目前有三种比较常见的方法。

方法一：特征值分解

只能作用于N * N的方矩阵，而实际User和Item的矩阵均不是方矩阵，所以不具有适用性；

方法二：奇异值分解

适用于所有M * N矩阵，但是对矩阵的稠密度要求高，现实中的矩阵都是稀疏的，如果需要使用必须把缺失的值通过近似值进行补全，一般通过平均值等方式；计算复杂度极高Ο(m∗n^2)。具体的数学计算逻辑较复杂，这里我们也不进行详细数学计算过程的展开了。因为奇异值分解方式对于计算资源要求极高而且要求矩阵必须是稠密的，所以实际在互联网场景中我们也不使用奇异值分解的方式。

方法三：梯度下降法

梯度下降法，2006年网飞举办的电影预测评分大赛上一位叫做 Simon Funk的选手提出一种新的方法叫做Funk SVD，后来又被称为LFM。梯度下降法矩阵分解引入了用户向量和物品向量，用q_{u}表示用户u的向量，p_{i}表示物品i的向量，利用用户向量与物品向量的内积q_{u}^{T}p_{i}来拟合用户对物品的评分r_{u,i}，利用梯度下降的方法来逐步迭代更新参数。目前工业界都使用方法三来进行矩阵分解。

三、隐语义模型的优缺点

对比上一篇文章里面介绍的协同过滤思想下的召回方法，隐语义模型具有哪些优缺点了。

3.1 优点

• 泛化能力强：隐语义模型同样需要依赖于数据，但是一定程度上可以缓解矩阵稀疏的问题；
• 计算空间复杂度低：矩阵分解最终生成的是用户向量、物品向量，其复杂度为(m+n)*k，而协同过滤所需维护的用户或物品相似度矩阵的复杂度为m*m或n*n，远远高于矩阵分解的复杂度；
• 更好的灵活性和扩展性：矩阵分解生成的用户向量、物品向量可以很好的与其他特征组合或拼接，也可以和深度学习神经网络相结合。

3.2 缺点

仅考虑了用户与物料各自的特征，不方便加入用户、物料与上下文的特征以及其他的一些交互特征，模型本身仍然具有一定局限性。

本文作者 @King James 。

版权声明

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处。如若内容有涉嫌抄袭侵权/违法违规/事实不符，请点击 举报 进行投诉反馈！