Menger定理
Menger定理
给出下面两种形式的定义:
- 点形式: 设顶点s和顶点t为图中不相邻的两个节点,则使它们分别属于不同的连通片所需要去除的顶点的最少数量等于连接顶点s和顶点t的独立简单路径的最大数目.
- 边形式: 所需要去除的边的最少数目等于连通顶点s和顶点t的不同相交的简单路径的最大数目.
下面定理中的术语:
两个节点之间独立简单路径: 所有路径只有起始节点是一样的,其他节点均不一样的, 独立简单路径之间互不相交
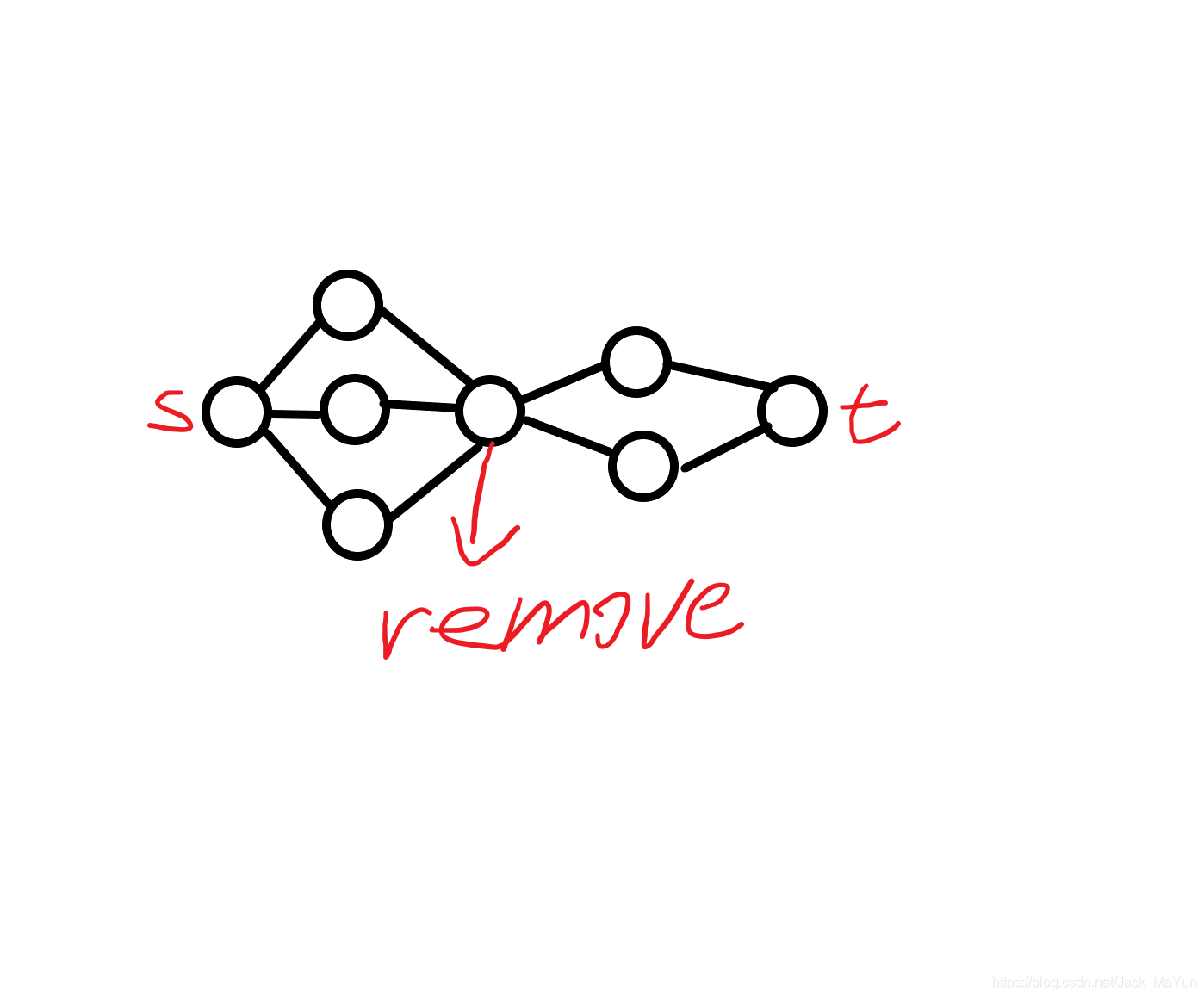
这样顶点s和t就分成了两个连通分量只需删除最中间的那个节点其独立简单路径也就只有一条满足menger定理
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!