分离轴定理解决矩形碰撞问题
引自http://www.gamedev.net/reference/programming/features/2dRotatedRectCollision/
2DRotated Rectangle Collision
Introduction
While working on a project for school,I found it necessary to perform a collision check between sprites that had beentranslated and rotated. I wanted to use bounding boxes because a per-pixelcheck was time consuming and unnecessary. After a couple of days of research Imanaged to work out an efficient solution using the separating axis theorem.After explaining my method to classmates and a few lab technicians, I realizedthat the game development community could benefit from a clear and thoroughexplanation of the process. Knowledge of linear algebra, specifically vectormath, is useful but not necessary for understanding this article.
Separating Axis Theorem
The separating axis theorem states thatfor a pair of convex polygons that are not in a state of collision there existsan axis perpendicular to an edge of one of the polygons that has no overlapbetween the projected vertices of the two polygons. Essentially, what thismeans is that if we project the vertices of the two polygons that we aretesting onto each axis that is perpendicular to the edges of each polygon andwe detect an overlap on each polygon there is a collision, if even one axisshows no overlap then a collision is impossible. This solution works for anycollision possibility, even the dreaded cross collision.

Figure 1. CrossCollision
Setting Up
Before we dive into the collision algorithmitself, there are a few prerequisites for this particular method. Firstly,although the separating axis theorem can be used to check for collisionsbetween any convex polygons, rectangles are the normal collision method in 2D,so I will assume that you are using rectangles. Additionally, I will assumethat you can convert your rectangles into a structure with four vectors, eachrepresenting a corner, and labeled or organized in such a way that you can tellwhich corner is which (specifically, we need to be able to identify whichcorners are adjacent – if the upper-left corner has been rotated until it is onthe bottom of the rectangle that’s fine, just so long as it remains connectedby an edge to the corners labeled upper-right and lower-left.).
The Method
The problem with checking for collision between two rotatedrectangles is really a matter of being able to decide when they’re notcolliding. The simple intersection test used by the Microsoft InteresectRect()function will check if the minimum and maximum x and y values of rectangle Bare within the minimum and maximum x and y values of rectangle A. This methodworks fine for axis-aligned rectangles, but when dealing with rotatedrectangles we need something a little more complex.
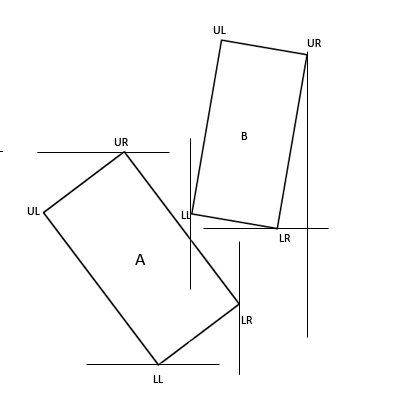
Figure 2.Standard Bounds-based Collision Check
As you can see, the minimum x value of B lies within thespace defined by the minimum and maximum x values of A. Additionally, theminimum y value of B lies within the space defined by the minimum and maximum yvalues of A. With simple bounds based collision detection this would registeras a collision, when it clearly is not.
Step 1
The first step in this method is to determine the axes that wewill be projecting our vertices onto. The separating axis theorem states thatwe must have an axis that is perpendicular to each of the edges of our twopolygons.
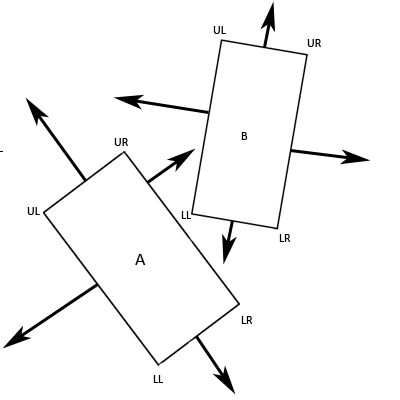
Figure 3. TheEight Perpendicular Axes
As you can see, we end up with eight axes. You should alsoimmediately see the benefits of using rectangles. Firstly, each edge has anopposite edge which shares an identical axis, we can take advantage of this tolower the number of axes that need checked to four. Secondly, the angle thatexists between any two adjacent edges on a rectangle is 90 degrees. As such, forany edge of a rectangle, both of the adjacent edges are perpendicular to it.This means that we can calculate our four axes to be as such:
Axis1.x = A.UR.x - A.UL.x
Axis1.y = A.UR.y - A.UL.y
Axis2.x = A.UR.x - A.LR.x
Axis2.y = A.UR.y - A.LR.y
Axis3.x = B.UL.x - B.LL.x
Axis3.y = B.UL.y - B.LL.y
Axis4.x = B.UL.x - B.UR.x
Axis4.y = B.UL.y - B.UR.y
Meaning that Axis 1 is the resultant vector of theupper-right corner of A minus the upper-left corner of A and so on. This givesus four axes, each of which is perpendicular to two opposite edges of one ofthe rectangles, meaning that for each edge we have an axis that isperpendicular to it.

Figure 4. OurFour Axes
Step 2
The next step is to project the vectors representing the fourcorners of each rectangle onto each of the axes. If you know how to do matrixprojections then you should have no problem doing this. If you understandvectors, but have forgotten how to do projections, then here is the equationfor the projection of rectangle A’s upper-right corner onto Axis 1:
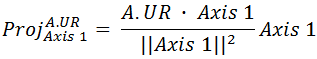
Here is the equation expanded out into scalar math andsimplified:
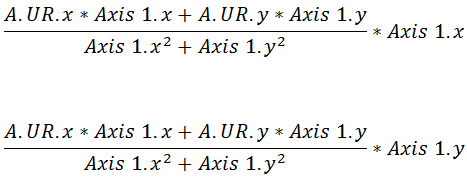
It is important to note that the only difference betweenthese two equations is that we’re multiplying by Axis 1’s x coordinate at the end of the first equation andwe’re multiplying by Axis 1’s ycoordinate at the end of the second equation. That will give you the x and ycoordinates of A.UR projected onto Axis 1. As an example, let’s pretend thatA.UR is at location (2, 6) and Axis 1 is represented by the vector (3, 4):

Therefore, in this example, the x coordinate of A.URprojected onto Axis 1 is 3.6 and the y coordinate is 4.8.
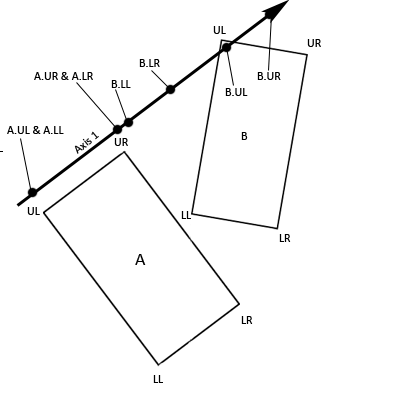
Figure 5.Vectors Projected Onto Axis 1
Step 3
The third step in this algorithm is to calculate scalar valuesthat will allow us to identify the maximum and minimum projected vectors foreach of the rectangles. While it might seem natural to use the norm (length) ofthe vectors, this won’t work as coordinates with negative values will return apositive scalar value. The simplest and cheapest solution is to take the dotproduct of each of the vectors and the axis. This will give us an essentiallymeaningless scalar value, however, this value will be indicative of thevector’s position on the axis. To use our above example:
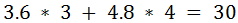
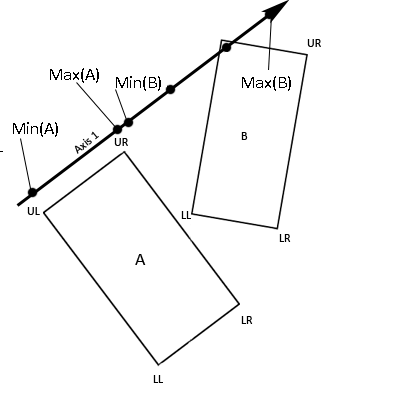
Figure 6. Theminimum and maximum scalar values
Step 4
Now identify the maximum and minimum scalar values (the ones thatwe just calculated) for rectangle A and rectangle B. If the minimum scalarvalue of B is less than or equal to the maximum scalar value of A and/or themaximum scalar value of B is greater than or equal to the minimum scalar valueof A then our objects overlap when projected onto this axis.
![]()

Figure 7. NoOverlap = No Collision
Repeat
Repeat steps 2, 3, and 4 for each of the axes. If all of the axesshow an overlap then there is a collision, if even one of the axes shows nooverlap then there is no collision.
Optimizations
There are a few things that can be done to optimize thisalgorithm:
You can and should stop checking forcollision the instant you find an axis where the rectangles don’t overlap.Remember, the separating axis theorem says that if two polygons are colliding allaxes that are perpendicular to the edges of the polygons will show an overlap.Meaning that, if one axis shows no overlap, then collision is not possible andyou should opt out to prevent unnecessary math.
It can really pay off to transform rectangle Binto rectangle A’s local space. In order to do this, you should maintain theserectangles in local space and then transform rectangle B into world space andthen by the inverse of rectangle A’s world space transform to put rectangle Binto rectangle A’s local space. Then, translate both rectangles equally so thatrectangle A is centered about the x and y axes. This means that two of the fouraxes that you need to project vectors onto are the unit (x and y) axes. Simplycheck for overlap between the x values of the corners of both rectangles andbetween the y values of the corners of both rectangles. With this solution youonly have to actually project the vectors onto arbitrary axes twice, instead offour times.
Figure 8.Rectangles A and B in world space
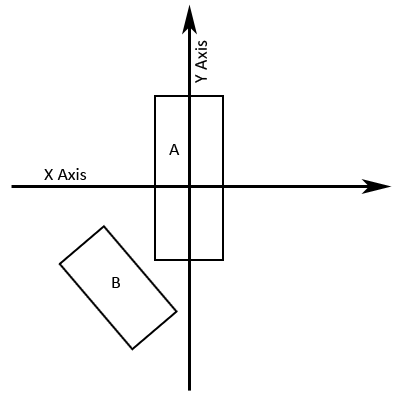
Figure 9.Rectangles A and B Transformed Into A's Local Space
It can be wise to utilize a radius thatcompletely encompasses the rectangle. If the distance between the centers ofrectangles A and B is greater than the radius of A and B added together thenthere cannot possibly be a collision and it is unnecessary to use theseparating axis theorem.
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!